Multiplication and Division

We begin with a review of what it means to multiply and divide signed numbers. The result of multiplying real numbers is called the productThe result of multiplying. and the result of dividing is called the quotientThe result after dividing.. Recall that multiplication is equivalent to adding:

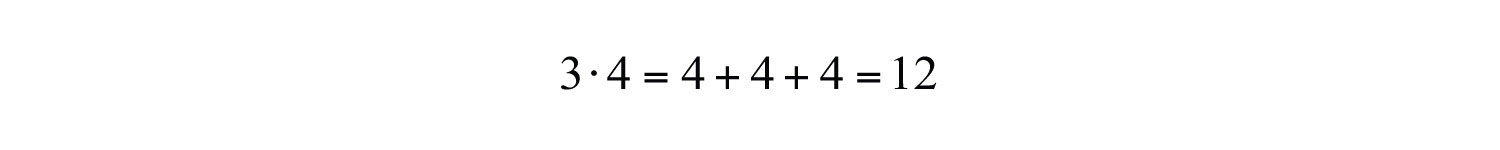
Clearly, the product of two positive numbers is positive. Similarly, the product of a positive number and negative number can be written as shown:

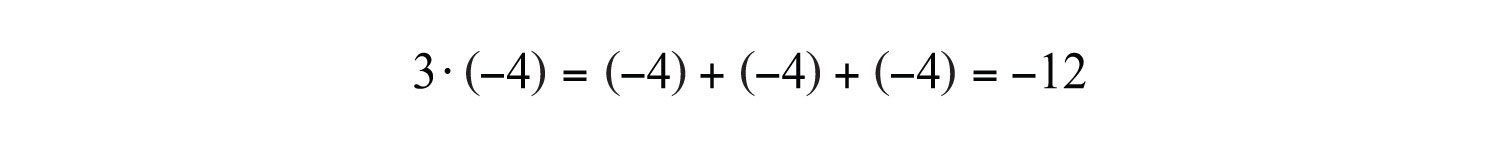
We see that the product of a positive number and a negative number is negative. Next, explore the results of multiplying two negative numbers. Consider the products in the following illustration and try to identify the pattern:

This shows that the product of two negative numbers is positive. To summarize,

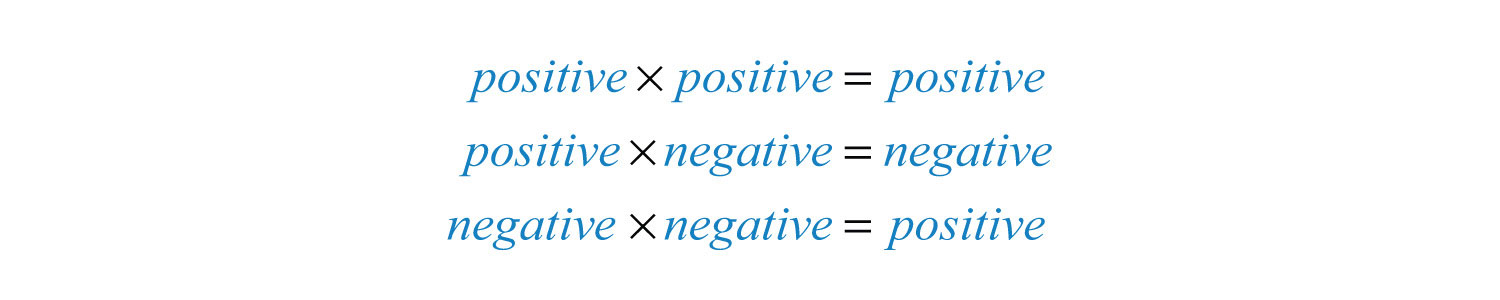
The rules for division are the same because division can always be rewritten as multiplication:

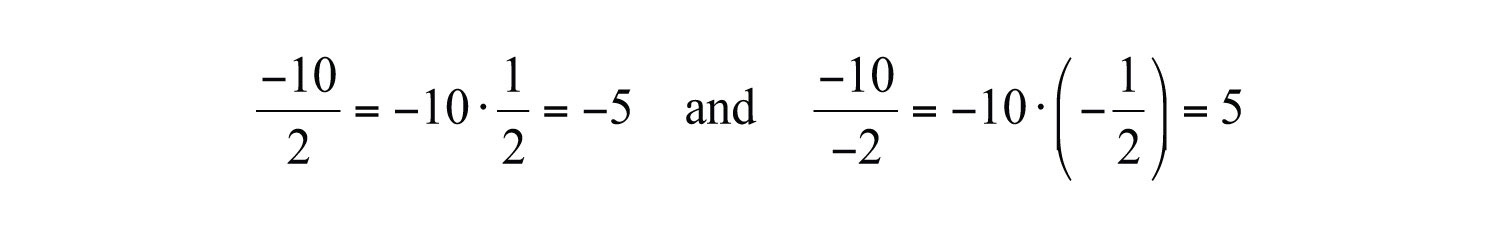
The rules for multiplication and division should not be confused with the fact that the sum of two negative numbers is negative.

Example 1: Simplify:

a. $\left(-3\right)+\left(-5\right)$

b. $\left(-3\right)\left(-5\right)$

Solution: Here we add and multiply the same two negative numbers.

a. The result of adding two negative numbers is negative.

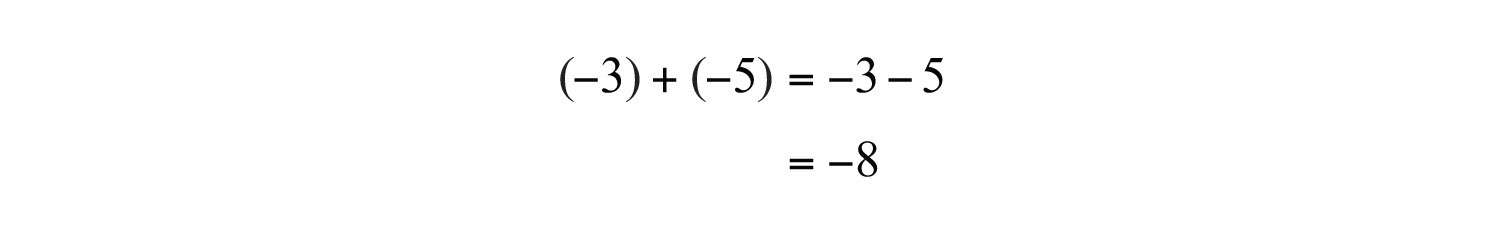
b. The result of multiplying two negative numbers is positive.

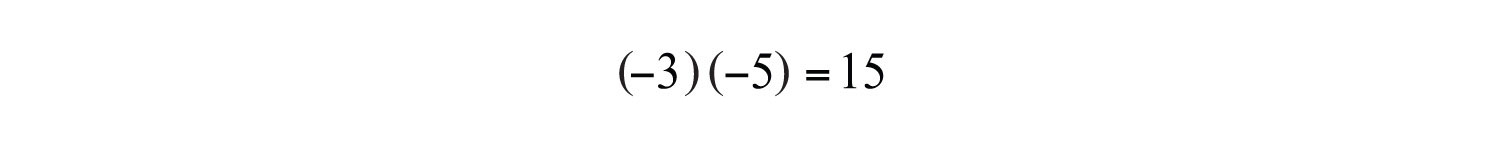
Answers: a. −8; b. 15

Given any real numbers a, b, and c, we have the following properties of multiplication:

Example 2: Simplify:

a. $5\cdot 0$

b. $10\cdot 1$

Solution:

a. Multiplying by zero results in zero.

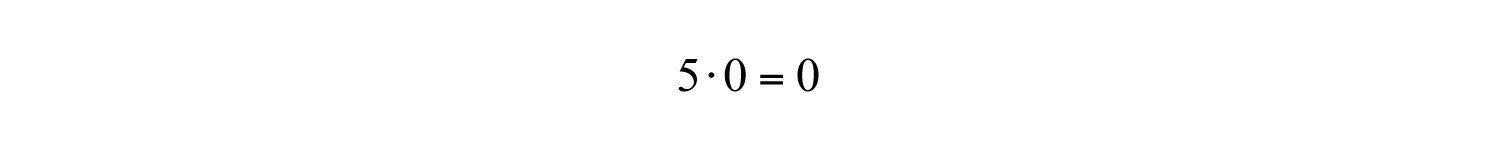
b. Multiplying any real number by one results in the same real number.

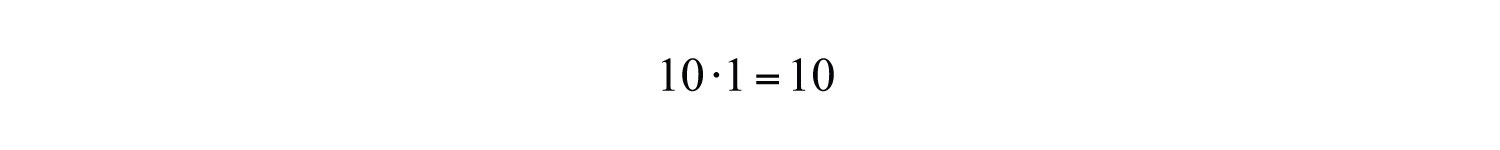
Answers: a. 0; b. 10

Example 3: Simplify:

a. $\left(3\cdot 7\right)\cdot 2$

b. $3\cdot \left(7\cdot 2\right)$

Solution:

a.

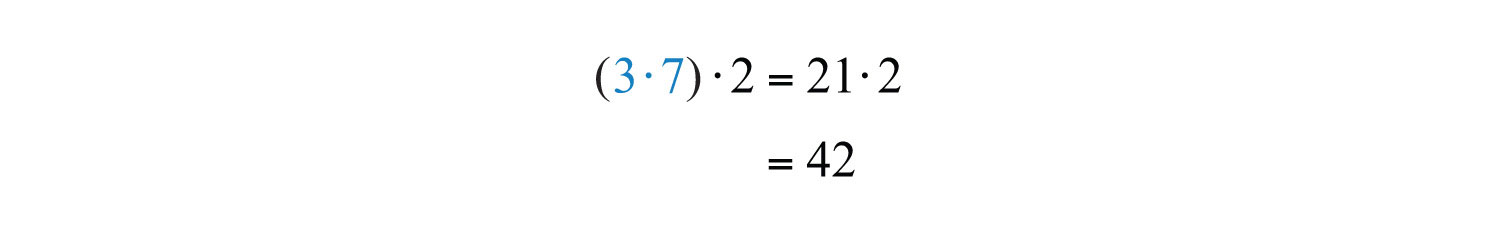
b.

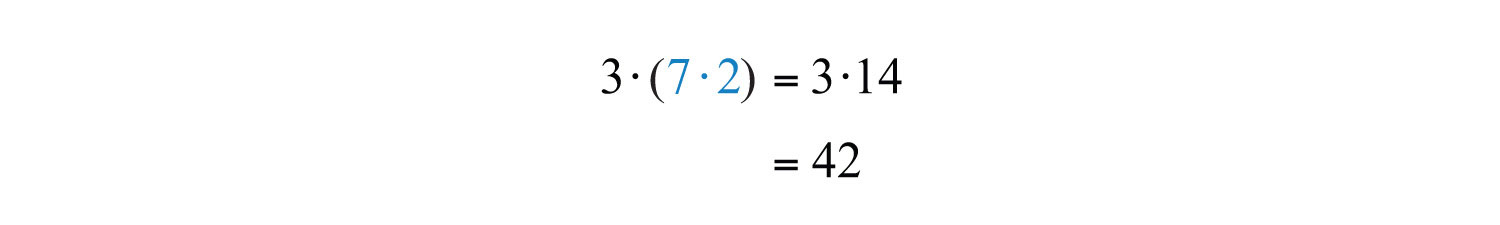
The value of each expression is 42. Changing the grouping of the numbers does not change the result.

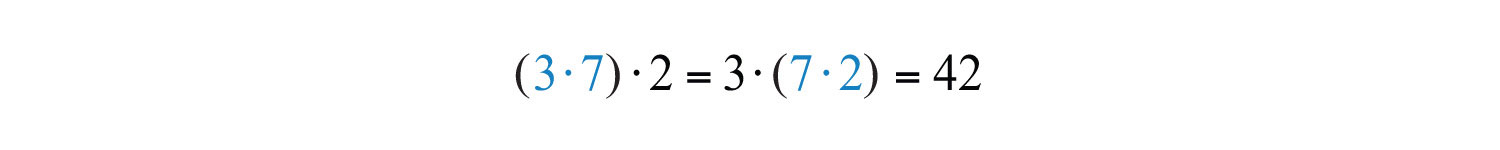
Answers: a. 42; b. 42

At this point, we highlight that multiplication is commutative: the order in which we multiply does not matter and yields the same result.

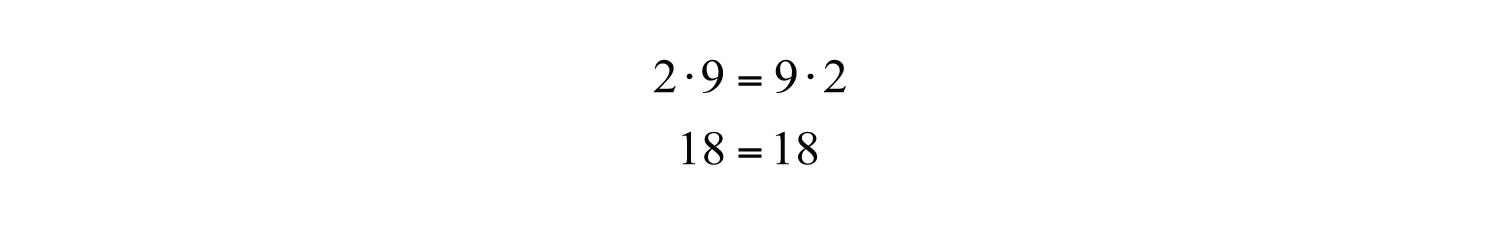
On the other hand, division is not commutative.

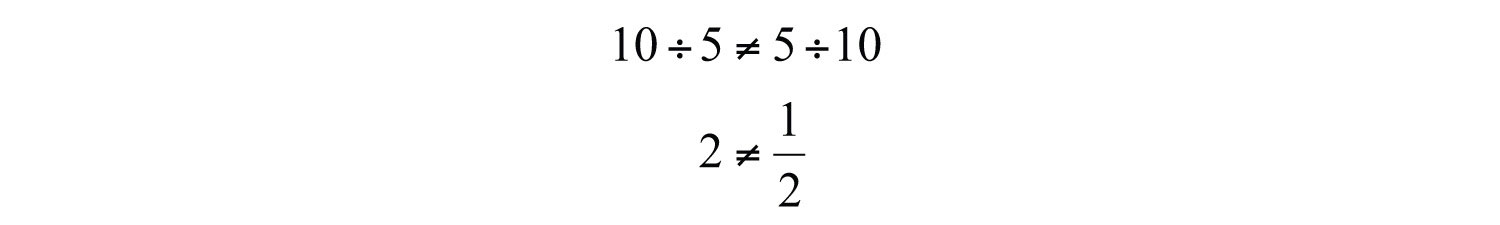
Use these properties to perform sequential operations involving multiplication and division. When doing so, it is important to perform these operations in order from left to right.

Example 4: Simplify: $3\left(-2\right)\left(-5\right)\left(-1\right)$.

Solution: Multiply two numbers at a time as follows:

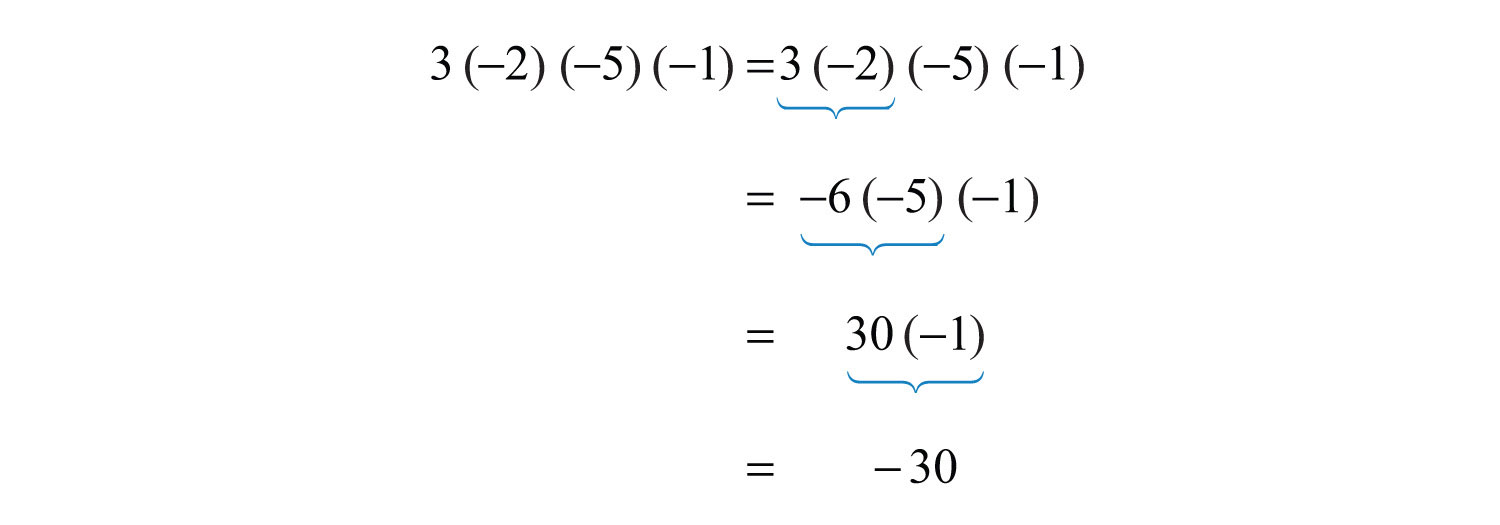
Answer: −30

Because multiplication is commutative, the order in which we multiply does not affect the final answer. When sequential operations involve multiplication and division, order does matter; hence we must work the operations from left to right to obtain a correct result.

Example 5: Simplify: $10÷\left(-2\right)\left(-5\right)$.

Solution: Perform the division first; otherwise, the result will be incorrect.

Answer: 25

Notice that the order in which we multiply and divide does affect the final result. Therefore, it is important to perform the operations of multiplication and division as they appear from left to right.

Example 6: Simplify: $-6\left(3\right)÷\left(-2\right)\left(-3\right)$.

Solution: Work the operations one at a time from left to right.

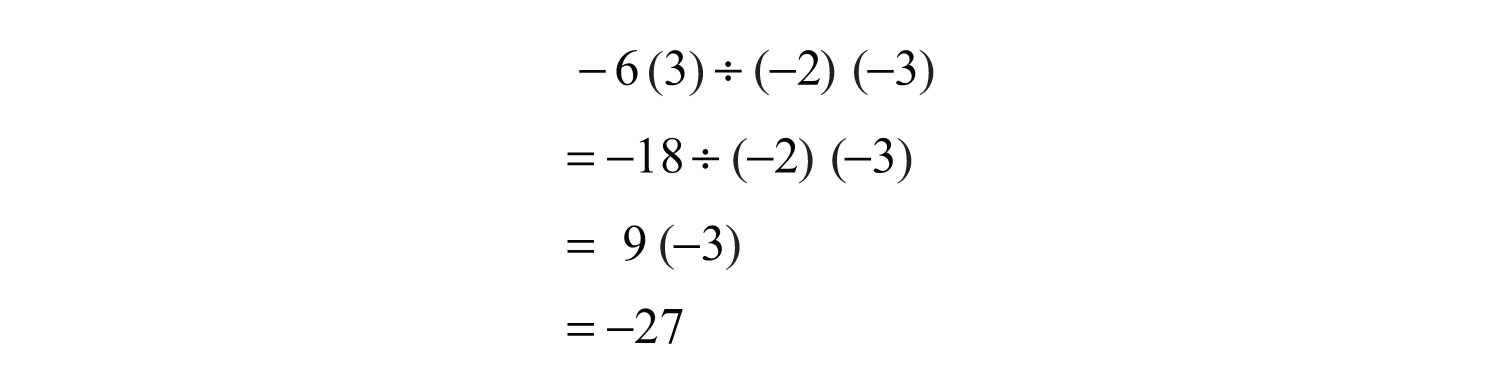
Try this! Simplify: $-5÷5\cdot 2\left(-3\right)$.

Answer: 6

Within text-based applications, the symbol used for multiplication is the asteriskThe symbol (*) that indicates multiplication within text-based applications. (*) and the symbol used for division is the forward slash (/).

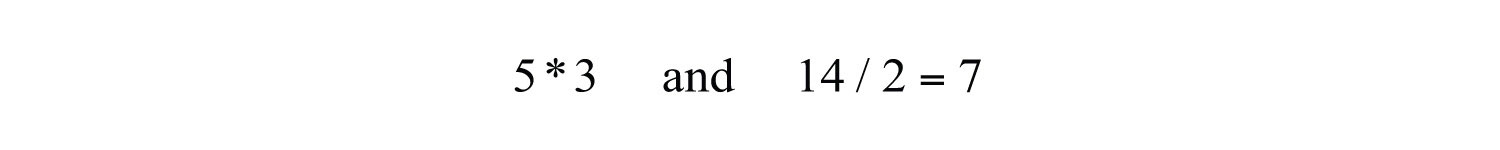
The set of even integersIntegers that are divisible by two or are multiples of two. is the set of all integers that are evenly divisible by 2. We can also obtain the set of even integers by multiplying each integer by 2.

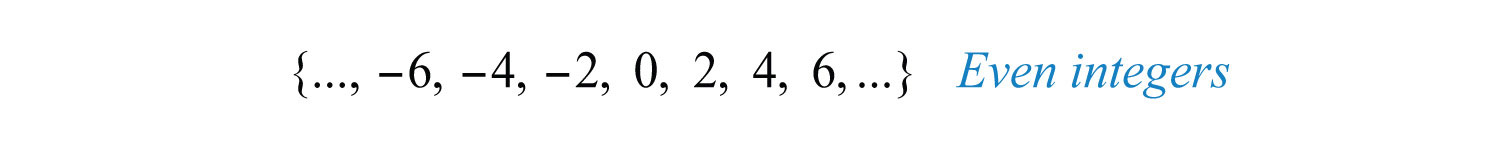
The set of odd integersIntegers that are not divisible by 2. is the set of all integers that are not evenly divisible by 2.

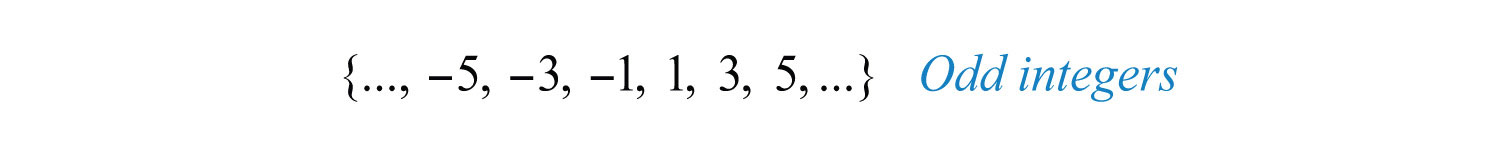
A prime numberIntegers greater than 1 that are divisible only by 1 and itself. is an integer greater than 1 that is divisible only by 1 and itself. The smallest prime number is 2 and the rest are necessarily odd.

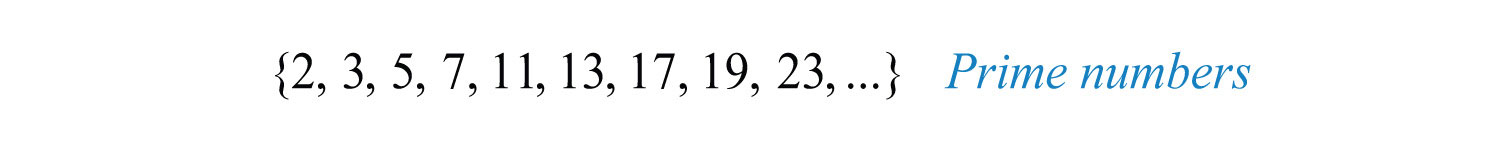
Any integer greater than 1 that is not prime is called a composite numberIntegers greater than 1 that are not prime. and can be written as a product of primes. When a composite number, such as 30, is written as a product, $30=2\cdot 15$, we say that $2\cdot 15$ is a factorizationAny combination of factors, multiplied together, resulting in the product. of 30 and that 2 and 15 are factorsAny of the numbers or expressions that form a product.. Note that factors divide the number evenly. We can continue to write composite factors as products until only a product of primes remains.

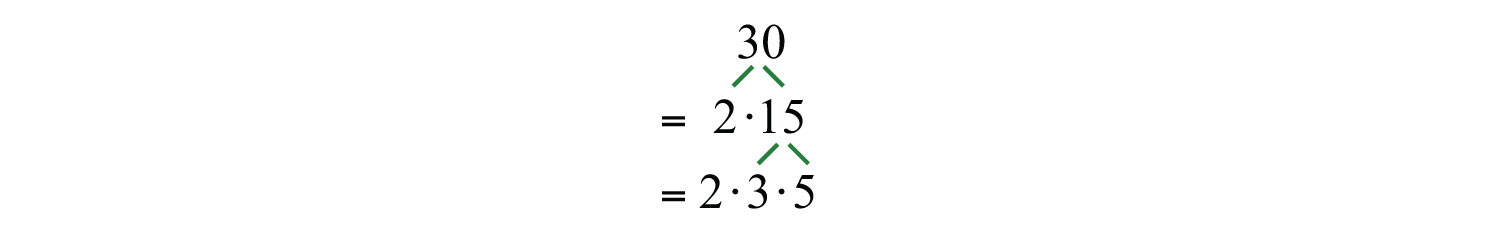
The prime factorizationThe unique factorization of a natural number written as a product of primes. of 30 is $2\cdot 3\cdot 5$.

Example 7: Determine the prime factorization of 70.

Solution: Begin by writing 70 as a product with 2 as a factor. Then express any composite factor as a product of prime numbers.

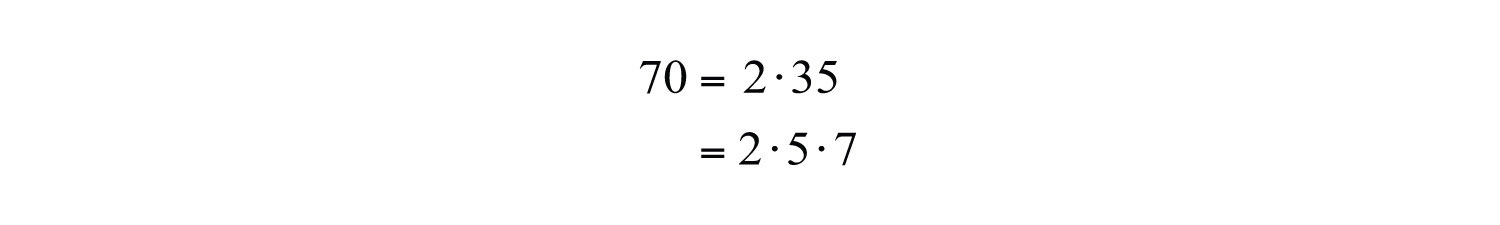
Since the prime factorization is unique, it does not matter how we choose to initially factor the number because the end result is the same.

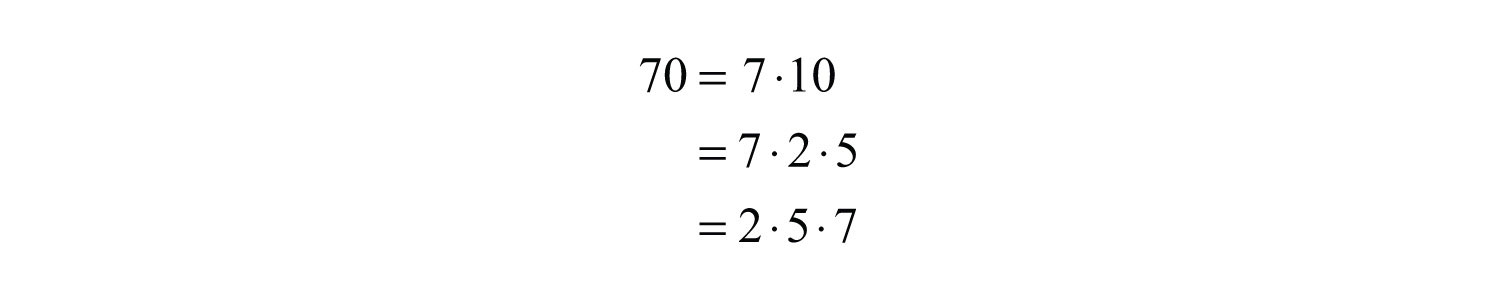
Answer: The prime factorization of 70 is $2\cdot 5\cdot 7$.

Some tests (called divisibility tests) useful for finding prime factors of composite numbers follow:

1. If the integer is even, then 2 is a factor.
2. If the sum of the digits is evenly divisible by 3, then 3 is a factor.
3. If the last digit is a 5 or 0, then 5 is a factor.

Often we find the need to translate English sentences that include multiplication and division terms to mathematical statements. Listed below are some key words that translate to the given operation.

Example 8: Calculate the quotient of 20 and −10.

Solution: The key word “quotient” implies that we should divide.

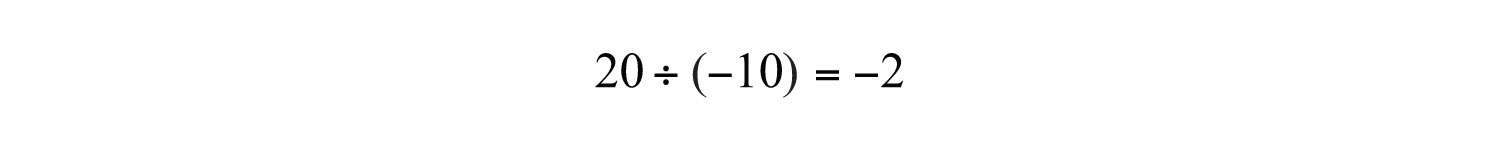
Answer: The quotient of 20 and −10 is −2.

Example 9: What is the product of the first three positive even integers?

Solution: The first three positive even integers are {2, 4, 6} and the key word “product” implies that we should multiply.

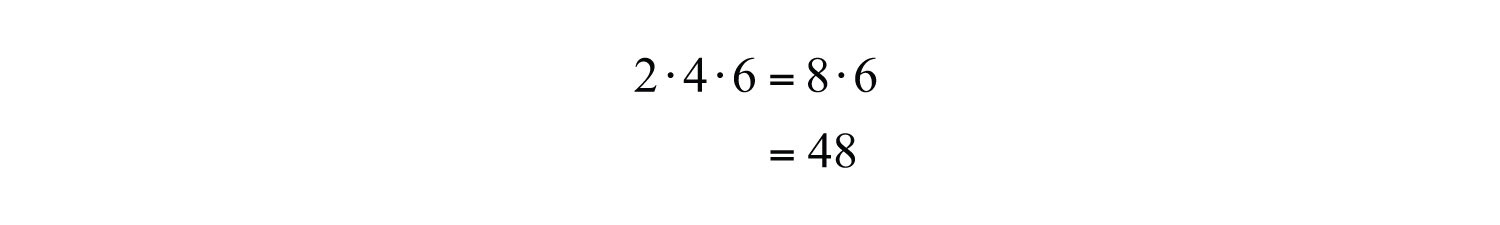
Answer: The product of the first three positive even integers is 48.

Example 10: Joe is able to drive 342 miles on 18 gallons of gasoline. How many miles per gallon of gas is this?

Solution: The key word “per” indicates that we must divide the number of miles driven by the number of gallons used:

Answer: Joe gets 19 miles per gallon from his vehicle.

In everyday life, we often wish to use a single value that typifies a set of values. One way to do this is to use what is called the arithmetic meanA numerical value that typifies a set of numbers. It is calculated by adding up the numbers in the set and dividing by the number of elements in the set. or averageUsed in reference to the arithmetic mean.. To calculate an average, divide the sum of the values in the set by the number of values in that set.

Example 11: A student earns 75, 86, and 94 on his first three exams. What is the student’s test average?

Solution: Add the scores and divide the sum by 3.

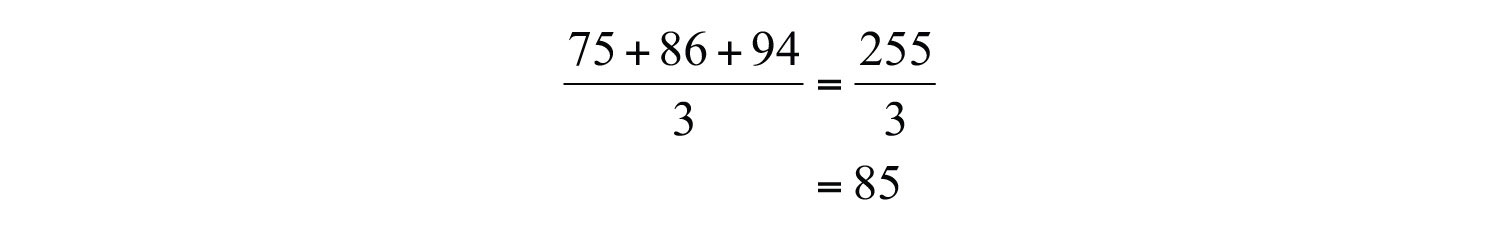
Answer: The student’s test average is 85.

Zero and Division

Recall the relationship between multiplication and division:

In this case, the dividendThe numerator of a quotient. 12 is evenly divided by the divisorThe denominator of a quotient. 6 to obtain the quotient, 2. It is true in general that if we multiply the divisor by the quotient we obtain the dividend. Now consider the case where the dividend is zero and the divisor is nonzero:

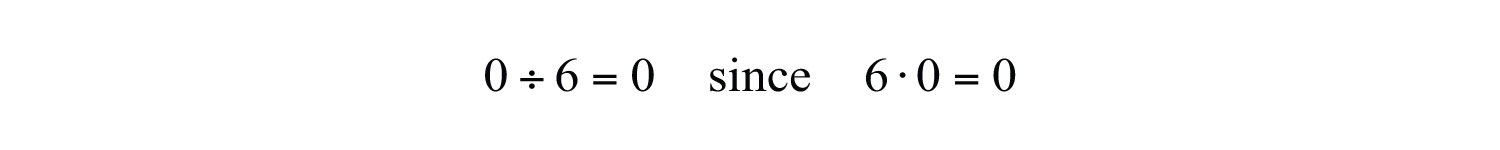
This demonstrates that zero divided by any nonzero real number must be zero. Now consider a nonzero number divided by zero:

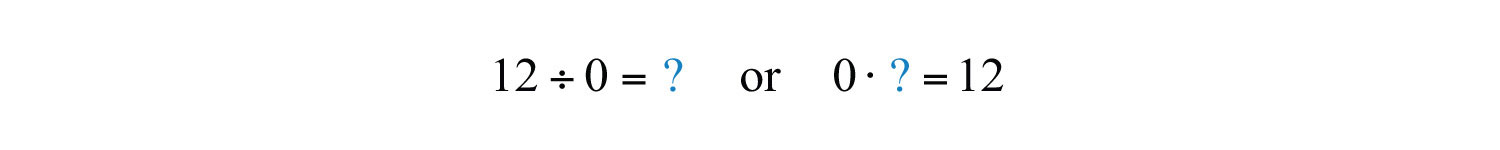
The zero-factor property of multiplication states that any real number times 0 is 0. We conclude that there is no real number such that $0\cdot ?=12$ and thus, the quotient is left undefinedA quotient such as $\frac{5}{0}$, which is left without meaning and is not assigned an interpretation.. Try $12÷0$ on a calculator. What does it say? For our purposes, we will simply write “undefined.”

To summarize, given any real number $a\ne 0$, then

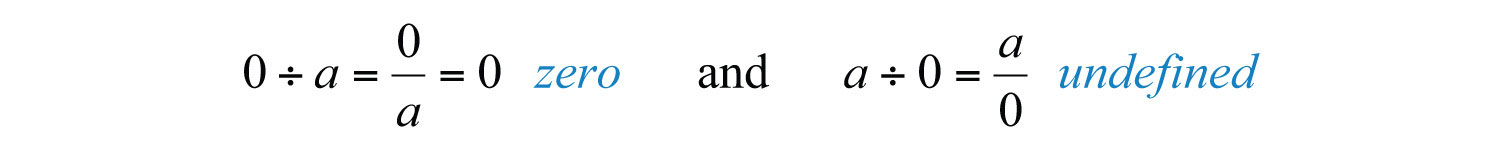
We are left to consider the case where the dividend and divisor are both zero.

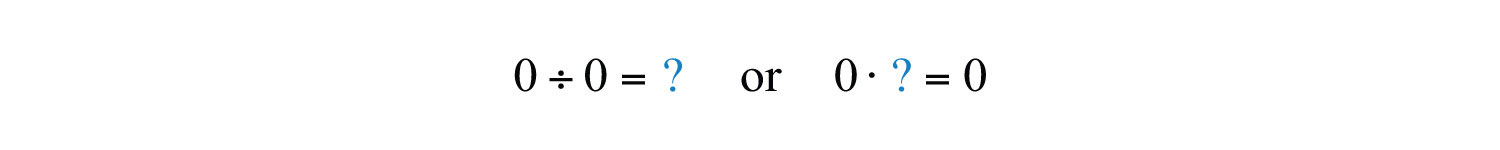
Here any real number seems to work. For example, $0\cdot 5=0$ and $0\cdot 3=0$. Therefore, the quotient is uncertain or indeterminateA quotient such as $\frac{0}{0}$, which is a quantity that is uncertain or ambiguous..

In this course, we state that $0÷0$ is undefined.