This is “Sequences, Series, and the Binomial Theorem”, chapter 9 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
Chapter 9 Sequences, Series, and the Binomial Theorem
9.1 Introduction to Sequences and Series
Learning Objectives
- Find any element of a sequence given a formula for its general term.
- Use sigma notation and expand corresponding series.
- Distinguish between a sequence and a series.
- Calculate the nth partial sum of sequence.
Sequences
A sequenceA function whose domain is a set of consecutive natural numbers starting with 1. is a function whose domain is a set of consecutive natural numbers beginning with 1. For example, the following equation with domain defines an infinite sequenceA sequence whose domain is the set of natural numbers :
The elements in the range of this function are called terms of the sequence. It is common to define the nth term, or the general term of a sequenceAn equation that defines the nth term of a sequence commonly denoted using subscripts , using the subscritped notation , which reads “a sub n.” Terms can be found using substitution as follows:
This produces an ordered list,
The ellipsis (…) indicates that this sequence continues forever. Unlike a set, order matters. If the domain of a sequence consists of natural numbers that end, such as , then it is called a finite sequenceA sequence whose domain is where k is a natural number..
Example 1
Given the general term of a sequence, find the first 5 terms as well as the 100th term:
Solution:
To find the first 5 terms, substitute 1, 2, 3, 4, and 5 for n and then simplify.
Use to determine the 100th term in the sequence.
Answer: First five terms: 0, 1, 3, 6, 10;
Sometimes the general term of a sequence will alternate in sign and have a variable other than n.
Example 2
Find the first 5 terms of the sequence:
Solution:
Here we take care to replace n with the first 5 natural numbers and not x.
Answer:
One interesting example is the Fibonacci sequence. The first two numbers in the Fibonacci sequence are 1, and each successive term is the sum of the previous two. Therefore, the general term is expressed in terms of the previous two as follows:
Here , , and A formula that describes a sequence in terms of its previous terms is called a recurrence relationA formula that uses previous terms of a sequence to describe subsequent terms..
Example 3
Find the first 7 Fibonacci numbers.
Solution:
Given that and , use the recurrence relation where is an integer starting with to find the next 5 terms:
Answer: 1, 1, 2, 3, 5, 8, 13
Figure 9.1

Leonardo Fibonacci (1170–1250) Wikipedia
Fibonacci numbers appear in applications ranging from art to computer science and biology. The beauty of this sequence can be visualized by constructing a Fibonacci spiral. Consider a tiling of squares where each side has a length that matches each Fibonacci number:
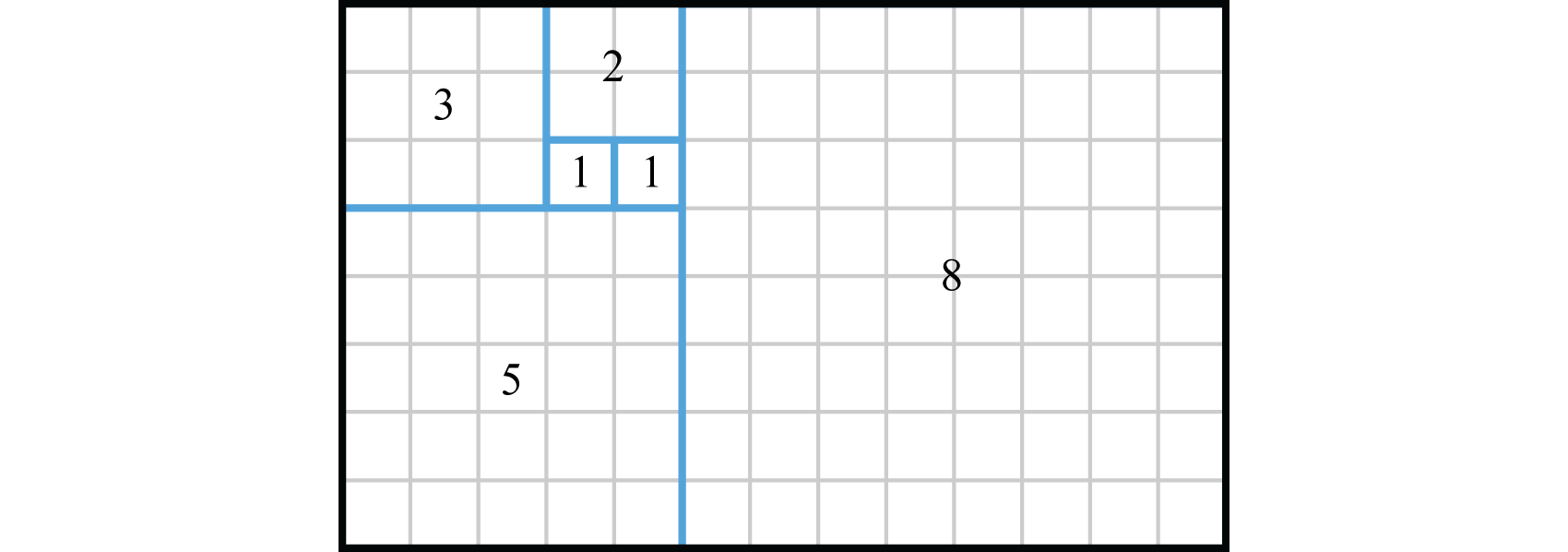
Connecting the opposite corners of the squares with an arc produces a special spiral shape.

This shape is called the Fibonacci spiral and approximates many spiral shapes found in nature.
Series
A seriesThe sum of the terms of a sequence. is the sum of the terms of a sequence. The sum of the terms of an infinite sequence results in an infinite seriesThe sum of the terms of an infinite sequence denoted , denoted The sum of the first n terms in a sequence is called a partial sumThe sum of the first n terms in a sequence denoted , denoted For example, given the sequence of positive odd integers 1, 3, 5,… we can write:
Example 4
Determine the 3rd and 5th partial sums of the sequence: 3,−6, 12,−24, 48,…
Solution:
Answer: ;
If the general term is known, then we can express a series using sigmaA sum denoted using the symbol (upper case Greek letter sigma). (or summationUsed when referring to sigma notation.) notation:
The symbol (upper case Greek letter sigma) is used to indicate a series. The expressions above and below indicate the range of the index of summationThe variable used in sigma notation to indicate the lower and upper bounds of the summation., in this case represented by n. The lower number indicates the starting integer and the upper value indicates the ending integer. The nth partial sum can be expressed using sigma notation as follows:
This is read, “the sum of as k goes from 1 to n.” Replace n with ∞ to indicate an infinite sum.
Example 5
Evaluate: .
Answer: 61
When working with sigma notation, the index does not always start at 1.
Example 6
Evaluate: .
Solution:
Here the index is expressed using the variable k, which ranges from 2 to 5.
Answer: −6
Infinity is used as the upper bound of a sum to indicate an infinite series.
Example 7
Write in expanded form: .
Solution:
In this case we begin with and add three dots to indicate that this series continues forever.
Answer:
When expanding a series, take care to replace only the variable indicated by the index.
Example 8
Write in expanded form: .
Solution:
Answer:
Key Takeaways
- A sequence is a function whose domain consists of a set of natural numbers beginning with 1. In addition, a sequence can be thought of as an ordered list.
- Formulas are often used to describe the nth term, or general term, of a sequence using the subscripted notation
- A series is the sum of the terms in a sequence. The sum of the first n terms is called the nth partial sum and is denoted
- Use sigma notation to denote summations in a compact manner. The nth partial sum, using sigma notation, can be written . The symbol denotes a summation where the expression below indicates that the index k starts at 1 and iterates through the natural numbers ending with the value n above.
Topic Exercises
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
where
-
where
-
where
-
where
-
where
-
where
-
where
-
where
-
where and
-
where and
-
where and
-
where and
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
An investment of $4,500 is made in an account earning 2% interest compounded quarterly. The balance in the account after n quarters is given by Find the amount in the account after each quarter for the first two years. Round to the nearest cent.
-
The value of a new car after n years is given by the formula Find and interpret Round to the nearest whole dollar.
-
The number of comparisons a computer algorithm makes to sort n names in a list is given by the formula Determine the number of comparisons it takes this algorithm to sort (2 million) names.
-
The number of comparisons a computer algorithm makes to search n names in a list is given by the formula Determine the number of comparisons it takes this algorithm to search (2 million) names.
Part A: Sequences
Find the first 5 terms of the sequence as well as the 30th term.
Find the first 5 terms of the sequence.
Find the first 5 terms of the sequence defined by the given recurrence relation.
Find the indicated term.
-
3, 5, 9, 17, 33,…;
-
−5, 7, −29, 79, −245,…;
-
4, 1, −4, −11, −20,…;
-
0, 2, 6, 12, 20,…;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
A structured settlement yields an amount in dollars each year, represented by n, according to the formula What is the total amount gained from the settlement after 5 years?
-
The first row of seating in a small theater consists of 14 seats. Each row thereafter consists of 2 more seats than the previous row. If there are 7 rows, how many total seats are in the theater?
Part B: Series
Find the indicated partial sum.
Evaluate.
Write in expanded form.
Express the following series using sigma notation.
-
Research and discuss Fibonacci numbers as they are found in nature.
-
Research and discuss the life and contributions of Leonardo Fibonacci.
-
Explain the difference between a sequence and a series. Provide an example of each.
Part C: Discussion Board
Answers
-
2, 4, 6, 8, 10;
-
-
0, , 4, , 12;
-
-
−4, 9, −16, 25, −36;
-
-
1, 3, 9, 27, 81;
-
-
, , , , ;
-
-
, , , , ;
-
-
2, , , , ;
-
-
-
-
-
-
-
-
-
-
3, 8, 13, 18, 23
-
-
−2, −6, −18, −54, −162
-
-
1, 2, 6, 24, 120
-
-
0, −1, −3, −7, −15
-
-
−1, 0, −1, −2, −5
-
-
1, 3, 2, −1, −3
-
-
−82
-
-
−500
-
-
-
-
32
-
-
Year 1: QI: $4,522.50; QII: $4,545.11; QIII: $4,567.84; QIV: $4,590.68; Year 2: QI: $4,613.63; QII: $4,636.70; QIII: $4,659.88; QIV: $4,683.18
-
-
Approximately comparisons
-
-
34
-
-
−30
-
-
−95
-
-
-
-
-
-
-
-
45
-
-
90
-
-
22
-
-
-
-
−22
-
-
15
-
-
22
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
$27,731
-
-
Answer may vary
-
-
Answer may vary
9.2 Arithmetic Sequences and Series
Learning Objectives
- Identify the common difference of an arithmetic sequence.
- Find a formula for the general term of an arithmetic sequence.
- Calculate the nth partial sum of an arithmetic sequence.
Arithmetic Sequences
An arithmetic sequenceA sequence of numbers where each successive number is the sum of the previous number and some constant d., or arithmetic progressionUsed when referring to an arithmetic sequence., is a sequence of numbers where each successive number is the sum of the previous number and some constant d.
And because , the constant d is called the common differenceThe constant d that is obtained from subtracting any two successive terms of an arithmetic sequence; . For example, the sequence of positive odd integers is an arithmetic sequence,
Here and the difference between any two successive terms is 2. We can construct the general term where,
In general, given the first term of an arithmetic sequence and its common difference d, we can write the following:
From this we see that any arithmetic sequence can be written in terms of its first element, common difference, and index as follows:
In fact, any general term that is linear in n defines an arithmetic sequence.
Example 1
Find an equation for the general term of the given arithmetic sequence and use it to calculate its 100th term:
Solution:
Begin by finding the common difference,
Note that the difference between any two successive terms is 3. The sequence is indeed an arithmetic progression where and
Therefore, we can write the general term Take a minute to verify that this equation describes the given sequence. Use this equation to find the 100th term:
Answer: ;
The common difference of an arithmetic sequence may be negative.
Example 2
Find an equation for the general term of the given arithmetic sequence and use it to calculate its 75th term:
Solution:
Begin by finding the common difference,
Next find the formula for the general term, here and
Therefore, and the 75th term can be calculated as follows:
Answer: ;
The terms between given terms of an arithmetic sequence are called arithmetic meansThe terms between given terms of an arithmetic sequence..
Example 3
Find all terms in between and of an arithmetic sequence. In other words, find all arithmetic means between the 1st and 7th terms.
Solution:
Begin by finding the common difference d. In this case, we are given the first and seventh term:
Substitute and into the above equation and then solve for the common difference d.
Next, use the first term and the common difference to find an equation for the nth term of the sequence.
With , where n is a positive integer, find the missing terms.
Answer: −5, −2, 1, 4, 7
In some cases, the first term of an arithmetic sequence may not be given.
Example 4
Find the general term of an arithmetic sequence where and
Solution:
To determine a formula for the general term we need and A linear system with these as variables can be formed using the given information and :
Eliminate by multiplying the first equation by −1 and add the result to the second equation.
Substitute into to find
Next, use the first term and the common difference to find a formula for the general term.
Answer:
Try this! Find an equation for the general term of the given arithmetic sequence and use it to calculate its 100th term:
Answer: ;
Arithmetic Series
An arithmetic seriesThe sum of the terms of an arithmetic sequence. is the sum of the terms of an arithmetic sequence. For example, the sum of the first 5 terms of the sequence defined by follows:
Adding 5 positive odd integers, as we have done above, is managable. However, consider adding the first 100 positive odd integers. This would be very tedious. Therefore, we next develop a formula that can be used to calculate the sum of the first n terms, denoted , of any arithmetic sequence. In general,
Writing this series in reverse we have,
And adding these two equations together, the terms involving d add to zero and we obtain n factors of :
Dividing both sides by 2 leads us the formula for the nth partial sum of an arithmetic sequenceThe sum of the first n terms of an arithmetic sequence given by the formula: :
Use this formula to calculate the sum of the first 100 terms of the sequence defined by Here and
Example 5
Find the sum of the first 50 terms of the given sequence: 4, 9, 14, 19, 24, …
Solution:
Determine whether or not there is a common difference between the given terms.
Note that the difference between any two successive terms is 5. The sequence is indeed an arithmetic progression and we can write
Therefore, the general term is To calculate the 50th partial sum of this sequence we need the 1st and the 50th terms:
Next use the formula to determine the 50th partial sum of the given arithmetic sequence.
Answer:
Example 6
Evaluate: .
Solution:
In this case, we are asked to find the sum of the first 35 terms of an arithmetic sequence with general term Use this to determine the 1st and the 35th term.
Next use the formula to determine the 35th partial sum.
Answer: −2,170
Example 7
The first row of seating in an outdoor amphitheater contains 26 seats, the second row contains 28 seats, the third row contains 30 seats, and so on. If there are 18 rows, what is the total seating capacity of the theater?
Figure 9.2

Roman Theater (Wikipedia)
Solution:
Begin by finding a formula that gives the number of seats in any row. Here the number of seats in each row forms a sequence:
Note that the difference between any two successive terms is 2. The sequence is an arithmetic progression where and
Therefore, the number of seats in each row is given by To calculate the total seating capacity of the 18 rows we need to calculate the 18th partial sum. To do this we need the 1st and the 18th terms:
Use this to calculate the 18th partial sum as follows:
Answer: There are 774 seats total.
Try this! Find the sum of the first 60 terms of the given sequence: 5, 0, −5, −10, −15, …
Answer:
Key Takeaways
- An arithmetic sequence is a sequence where the difference d between successive terms is constant.
- The general term of an arithmetic sequence can be written in terms of its first term , common difference d, and index n as follows:
- An arithmetic series is the sum of the terms of an arithmetic sequence.
- The nth partial sum of an arithmetic sequence can be calculated using the first and last terms as follows:
Topic Exercises
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
3, 9, 15, 21, 27,…
-
3, 8, 13, 18, 23,…
-
−3, −7, −11, −15, −19,…
-
−6, −14, −22, −30, −38,…
-
−5, −10, −15, −20, −25,…
-
2, 4, 6, 8, 10,…
-
, , , , ,…
-
, , , , ,…
-
, 0, , , −1,…
-
, , , −2, ,…
-
0.8, 2, 3.2, 4.4, 5.6,…
-
4.4, 7.5, 10.6, 13.7, 16.8,…
-
Find the 50th positive odd integer.
-
Find the 50th positive even integer.
-
Find the 40th term in the sequence that consists of every other positive odd integer: 1, 5, 9, 13,…
-
Find the 40th term in the sequence that consists of every other positive even integer: 2, 6, 10, 14,…
-
What number is the term 355 in the arithmetic sequence −15, −5, 5, 15, 25,…?
-
What number is the term −172 in the arithmetic sequence 4, −4, −12, −20, −28,…?
-
Given the arithmetic sequence defined by the recurrence relation where and , find an equation that gives the general term in terms of and the common difference d.
-
Given the arithmetic sequence defined by the recurrence relation where and , find an equation that gives the general term in terms of and the common difference d.
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
Part A: Arithmetic Sequences
Write the first 5 terms of the arithmetic sequence given its first term and common difference. Find a formula for its general term.
Given the arithmetic sequence, find a formula for the general term and use it to determine the 100th term.
Given the terms of an arithmetic sequence, find a formula for the general term.
Find all arithmetic means between the given terms.
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
-
-
-
-
-
-
-
-
-
-
Find the sum of the first 200 positive integers.
-
Find the sum of the first 400 positive integers.
-
The sum of the first 50 positive odd integers.
-
The sum of the first 200 positive odd integers.
-
The sum of the first 50 positive even integers.
-
The sum of the first 200 positive even integers.
-
The sum of the first k positive odd integers.
-
The sum of the first k positive even integers.
-
The first row of seating in a small theater consists of 8 seats. Each row thereafter consists of 3 more seats than the previous row. If there are 12 rows, how many total seats are in the theater?
-
The first row of seating in an outdoor amphitheater contains 42 seats, the second row contains 44 seats, the third row contains 46 seats, and so on. If there are 22 rows, what is the total seating capacity of the theater?
-
If a triangular stack of bricks has 37 bricks on the bottom row, 34 bricks on the second row and so on with one brick on top. How many bricks are in the stack?
-
Each successive row of a triangular stack of bricks has one less brick until there is only one brick on top. How many rows does the stack have if there are 210 total bricks?
-
A 10-year salary contract offers $65,000 for the first year with a $3,200 increase each additional year. Determine the total salary obligation over the 10 year period.
-
A clock tower strikes its bell the number of times indicated by the hour. At one o’clock it strikes once, at two o’clock it strikes twice and so on. How many times does the clock tower strike its bell in a day?
Part B: Arithmetic Series
Calculate the indicated sum given the formula for the general term.
Evaluate.
The general term for the sequence of positive odd integers is given by and the general term for the sequence of positive even integers is given by Find the following.
-
Is the Fibonacci sequence an arithmetic sequence? Explain.
-
Use the formula for the nth partial sum of an arithmetic sequence and the formula for the general term to derive a new formula for the nth partial sum Under what circumstances would this formula be useful? Explain using an example of your own making.
-
Discuss methods for calculating sums where the index does not start at 1. For example,
-
A famous story involves Carl Friedrich Gauss misbehaving at school. As punishment, his teacher assigned him the task of adding the first 100 integers. The legend is that young Gauss answered correctly within seconds. What is the answer and how do you think he was able to find the sum so quickly?
Part C: Discussion Board
Answers
-
5, 8, 11, 14, 17;
-
-
15, 10, 5, 0, −5;
-
-
, , , , ;
-
-
1, , 0, , −1;
-
-
1.8, 2.4, 3, 3.6, 4.2;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
99
-
-
157
-
-
38
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1, 5, 9, 13
-
-
, 5, , 6,
-
-
18
-
-
15,650
-
-
−2,450
-
-
90
-
-
−7,800
-
-
−4,230
-
-
38,640
-
-
124,750
-
-
−18,550
-
-
−765
-
-
10,578
-
-
20,100
-
-
2,500
-
-
2,550
-
-
-
-
294 seats
-
-
247 bricks
-
-
$794,000
-
-
Answer may vary
-
-
Answer may vary
-
9.3 Geometric Sequences and Series
Learning Objectives
- Identify the common ratio of a geometric sequence.
- Find a formula for the general term of a geometric sequence.
- Calculate the nth partial sum of a geometric sequence.
- Calculate the sum of an infinite geometric series when it exists.
Geometric Sequences
A geometric sequenceA sequence of numbers where each successive number is the product of the previous number and some constant r., or geometric progressionUsed when referring to a geometric sequence., is a sequence of numbers where each successive number is the product of the previous number and some constant r.
And because , the constant factor r is called the common ratioThe constant r that is obtained from dividing any two successive terms of a geometric sequence; . For example, the following is a geometric sequence,
Here and the ratio between any two successive terms is 3. We can construct the general term where,
In general, given the first term and the common ratio r of a geometric sequence we can write the following:
From this we see that any geometric sequence can be written in terms of its first element, its common ratio, and the index as follows:
In fact, any general term that is exponential in n is a geometric sequence.
Example 1
Find an equation for the general term of the given geometric sequence and use it to calculate its 10th term:
Solution:
Begin by finding the common ratio,
Note that the ratio between any two successive terms is 2. The sequence is indeed a geometric progression where and
Therefore, we can write the general term and the 10th term can be calculated as follows:
Answer: ;
The terms between given terms of a geometric sequence are called geometric meansThe terms between given terms of a geometric sequence..
Example 2
Find all terms between and of a geometric sequence. In other words, find all geometric means between the 1st and 4th terms.
Solution:
Begin by finding the common ratio r. In this case, we are given the first and fourth terms:
Substitute and into the above equation and then solve for r.
Next use the first term and the common ratio to find an equation for the nth term of the sequence.
Now we can use where n is a positive integer to determine the missing terms.
Answer: −15, −45,
The first term of a geometric sequence may not be given.
Example 3
Find the general term of a geometric sequence where and
Solution:
To determine a formula for the general term we need and A nonlinear system with these as variables can be formed using the given information and :
Solve for in the first equation,
Substitute into the second equation and solve for r.
Back substitute to find :
Therefore, and
Answer:
Try this! Find an equation for the general term of the given geometric sequence and use it to calculate its 6th term:
Answer: ;
Geometric Series
A geometric seriesThe sum of the terms of a geometric sequence. is the sum of the terms of a geometric sequence. For example, the sum of the first 5 terms of the geometric sequence defined by follows:
Adding 5 positive integers is managable. However, the task of adding a large number of terms is not. Therefore, we next develop a formula that can be used to calculate the sum of the first n terms of any geometric sequence. In general,
Multiplying both sides by r we can write,
Subtracting these two equations we then obtain,
Assuming dividing both sides by leads us to the formula for the nth partial sum of a geometric sequenceThe sum of the first n terms of a geometric sequence, given by the formula: , :
In other words, the nth partial sum of any geometric sequence can be calculated using the first term and the common ratio. For example, to calculate the sum of the first 15 terms of the geometric sequence defined by , use the formula with and
Example 4
Find the sum of the first 10 terms of the given sequence: 4, −8, 16, −32, 64,…
Solution:
Determine whether or not there is a common ratio between the given terms.
Note that the ratio between any two successive terms is −2; hence, the given sequence is a geometric sequence. Use and the fact that to calculate the sum of the first 10 terms,
Answer:
Example 5
Evaluate: .
Solution:
In this case, we are asked to find the sum of the first 6 terms of a geometric sequence with general term Use this to determine the 1st term and the common ratio r:
To show that there is a common ratio we can use successive terms in general as follows:
Use and to calculate the 6th partial sum.
Answer: 26,040
Try this! Find the sum of the first 9 terms of the given sequence: −2, 1, −1/2,…
Answer:
If the common ratio r of an infinite geometric sequence is a fraction where (that is ), then the factor found in the formula for the nth partial sum tends toward 1 as n increases. For example, if and we have,
Here we can see that this factor gets closer and closer to 1 for increasingly larger values of n. This illustrates the idea of a limit, an important concept used extensively in higher-level mathematics, which is expressed using the following notation:
This is read, “the limit of as n approaches infinity equals 1.” While this gives a preview of what is to come in your continuing study of mathematics, at this point we are concerned with developing a formula for special infinite geometric series. Consider the nth partial sum of any geometric sequence,
If then the limit of the partial sums as n approaches infinity exists and we can write,
Therefore, a convergent geometric seriesAn infinite geometric series where whose sum is given by the formula: is an infinite geometric series where ; its sum can be calculated using the formula:
Example 6
Find the sum of the infinite geometric series:
Solution:
Determine the common ratio,
Since the common ratio is a fraction between −1 and 1, this is a convergent geometric series. Use the first term and the common ratio to calculate its sum.
Answer:
Note: In the case of an infinite geometric series where , the series diverges and we say that there is no sum. For example, if then and we have
We can see that this sum grows without bound and has no sum.
A repeating decimal can be written as an infinite geometric series whose common ratio is a power of 1/10. Therefore, the formula for a convergent geometric series can be used to convert a repeating decimal into a fraction.
Example 7
Write as a fraction:
Solution:
Begin by identifying the repeating digits to the right of the decimal and rewrite it as a geometric progression.
In this form we can determine the common ratio,
Note that the ratio between any two successive terms is . Use this and the fact that to calculate the infinite sum:
Therefore, and we have,
Answer:
Example 8
A certain ball bounces back to two-thirds of the height it fell from. If this ball is initially dropped from 27 feet, approximate the total distance the ball travels.
Solution:
We can calculate the height of each successive bounce:
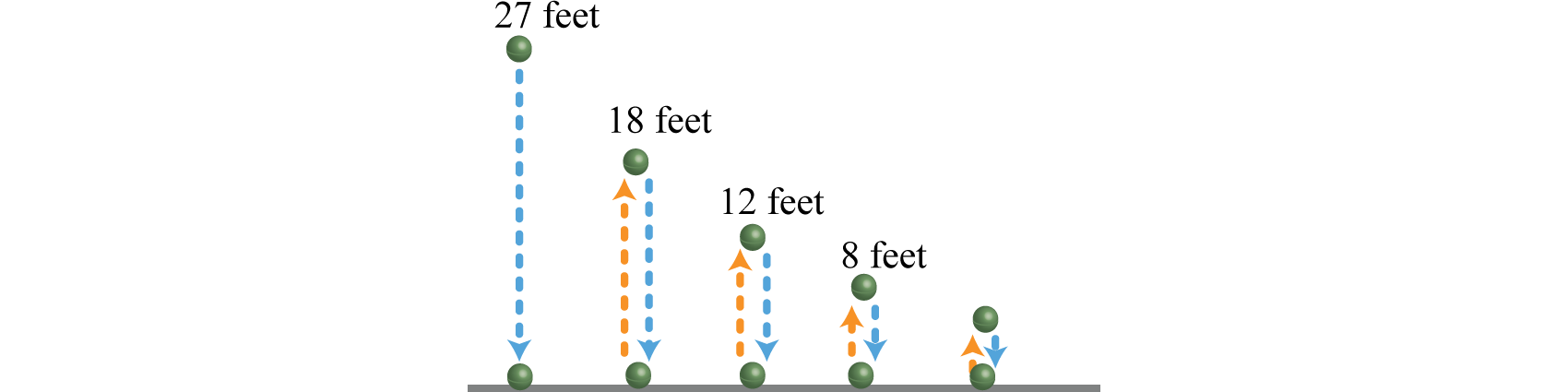
The total distance that the ball travels is the sum of the distances the ball is falling and the distances the ball is rising. The distances the ball falls forms a geometric series,
where and Because r is a fraction between −1 and 1, this sum can be calculated as follows:
Therefore, the ball is falling a total distance of 81 feet. The distances the ball rises forms a geometric series,
where and . Calculate this sum in a similar manner:
Therefore, the ball is rising a total distance of 54 feet. Approximate the total distance traveled by adding the total rising and falling distances:
Answer: 135 feet
Key Takeaways
- A geometric sequence is a sequence where the ratio r between successive terms is constant.
- The general term of a geometric sequence can be written in terms of its first term , common ratio r, and index n as follows:
- A geometric series is the sum of the terms of a geometric sequence.
- The nth partial sum of a geometric sequence can be calculated using the first term and common ratio r as follows:
- The infinite sum of a geometric sequence can be calculated if the common ratio is a fraction between −1 and 1 (that is ) as follows: If , then no sum exists.
Topic Exercises
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
7, 28, 112,…
-
−2, −10, −50,…
-
2, , ,…
-
1, , ,…
-
8, 4, 2,…
-
6, 2, ,…
-
−1, , ,…
-
2, , ,…
-
, −2, 12,…
-
, −2, 10,…
-
−3.6, −4.32, −5.184,…
-
0.8, −2.08, 5.408,…
-
Find the general term and use it to determine the 20th term in the sequence: ,…
-
Find the general term and use it to determine the 20th term in the sequence: ,…
-
The number of cells in a culture of a certain bacteria doubles every 4 hours. If 200 cells are initially present, write a sequence that shows the population of cells after every nth 4-hour period for one day. Write a formula that gives the number of cells after any 4-hour period.
-
A certain ball bounces back at one-half of the height it fell from. If this ball is initially dropped from 12 feet, find a formula that gives the height of the ball on the nth bounce and use it to find the height of the ball on the 6th bounce.
-
Given a geometric sequence defined by the recurrence relation where and , find an equation that gives the general term in terms of and the common ratio r.
-
Given the geometric sequence defined by the recurrence relation where and , find an equation that gives the general term in terms of and the common ratio r.
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
Part A: Geometric Sequences
Write the first 5 terms of the geometric sequence given its first term and common ratio. Find a formula for its general term.
Given the geometric sequence, find a formula for the general term and use it to determine the 5th term in the sequence.
Given the terms of a geometric sequence, find a formula for the general term.
Find all geometric means between the given terms.
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
-
-
-
-
-
-
-
-
;
-
;
-
;
-
;
-
;
-
;
-
-
-
-
-
-
-
1.222…
-
5.777 …
-
2.252525…
-
3.272727…
-
1.999…
-
1.090909…
-
Suppose you agreed to work for pennies a day for 30 days. You will earn 1 penny on the first day, 2 pennies the second day, 4 pennies the third day, and so on. How many total pennies will you have earned at the end of the 30 day period? What is the dollar amount?
-
An initial roulette wager of $100 is placed (on red) and lost. To make up the difference, the player doubles the bet and places a $200 wager and loses. Again, to make up the difference, the player doubles the wager to $400 and loses. If the player continues doubling his bet in this manner and loses 7 times in a row, how much will he have lost in total?
-
A certain ball bounces back to one-half of the height it fell from. If this ball is initially dropped from 12 feet, approximate the total distance the ball travels.
-
A golf ball bounces back off of a cement sidewalk three-quarters of the height it fell from. If the ball is initially dropped from 8 meters, approximate the total distance the ball travels.
-
A structured settlement yields an amount in dollars each year, represented by n, according to the formula What is the total amount gained from the settlement after 10 years?
-
Beginning with a square, where each side measures 1 unit, inscribe another square by connecting the midpoints of each side. Continue inscribing squares in this manner indefinitely, as pictured:

Find the sum of the area of all squares in the figure. (Hint: Begin by finding the sequence formed using the areas of each square.)
Part B: Geometric Series
Calculate the indicated sum.
Write as a mixed number.
-
-
-
-
-
-
-
-
-
-
-
-
-
1, −1, 1, −1,…
-
0, 0, 0,…
-
;
-
;
-
;
-
;
-
;
-
;
-
-
-
-
-
-
Part C: Sequences and Series
Categorize the sequence as arithmetic, geometric, or neither. Give the common difference or ratio, if it exists.
Categorize the sequence as arithmetic or geometric, and then calculate the indicated sum.
Calculate the indicated sum.
-
Use the techniques found in this section to explain why
-
Construct a geometric sequence where Explore the nth partial sum of such a sequence. What conclusions can we make?
Part D: Discussion Board
Answers
-
1, 5, 25, 125, 625;
-
-
2, 6, 18, 54, 162;
-
-
2, −6, 18, −54, 162;
-
-
3, 2, , , ;
-
-
1.2, 0.72, 0.432, 0.2592, 0.15552;
-
-
,
-
-
,
-
-
,
-
-
,
-
-
,
-
-
,
-
-
;
-
-
400 cells; 800 cells; 1,600 cells; 3,200 cells; 6,400 cells; 12,800 cells; cells
-
-
-
-
-
-
-
-
-
-
-
-
-
-
10, 50
-
-
−200; −2,000
-
-
16,380
-
-
-
-
305
-
-
-
-
3,905
-
-
4,092
-
-
−177,144
-
-
-
-
-
-
-
-
−1
-
-
3
-
-
No sum
-
-
-
-
-
-
-
-
2
-
-
1,073,741,823 pennies; $10,737,418.23
-
-
36 feet
-
-
$26,778.77
-
-
Geometric;
-
-
Arithmetic;
-
-
Neither
-
-
Arithmetic;
-
-
Neither
-
-
Geometric;
-
-
Geometric;
-
-
Geometric; 292,968
-
-
Arithmetic; 210
-
-
Geometric;
-
-
3,575
-
-
−1,365
-
-
200
-
-
Answer may vary
-
9.4 Binomial Theorem
Learning Objectives
- Evaluate expressions involving factorials.
- Calculate binomial coefficients.
- Expand powers of binomials using the binomial theorem.
Factorials and the Binomial Coefficient
We begin by defining the factorialThe product of all natural numbers less than or equal to a given natural number, denoted n!. of a natural number n, denoted n!, as the product of all natural numbers less than or equal to n.
For example,
We define zero factorialThe factorial of zero is defined to be equal to 1; to be equal to 1,
The factorial of a negative number is not defined.
Note: On most modern calculators you will find a factorial function. Some calculators do not provide a button dedicated to it. However, it usually can be found in the menu system if one is provided.
The factorial can also be expressed using the following recurrence relation,
For example, the factorial of 8 can be expressed as the product of 8 and 7!:
When working with ratios involving factorials, it is often the case that many of the factors cancel.
Example 1
Evaluate: .
Solution:
Answer: 665,280
The binomial coefficientAn integer that is calculated using the formula: , denoted , is read “n choose k” and is given by the following formula:
This formula is very important in a branch of mathematics called combinatorics. It gives the number of ways k elements can be chosen from a set of n elements where order does not matter. In this section, we are concerned with the ability to calculate this quantity.
Example 2
Calculate: .
Solution:
Use the formula for the binomial coefficent,
where and After substituting, look for factors to cancel.
Answer: 35
Note: Check the menu system of your calculator for a function that calculates this quantity. Look for the notation in the probability subsection.
Consider the following binomial raised to the 3rd power in its expanded form:
Compare it to the following calculations,
Notice that there appears to be a connection between these calculations and the coefficients of the expanded binomial. This observation is generalized in the next section.
Binomial Theorem
Consider expanding :
One quickly realizes that this is a very tedious calculation involving multiple applications of the distributive property. The binomial theoremDescribes the algebraic expansion of binomials raised to powers: provides a method of expanding binomials raised to powers without directly multiplying each factor:
More compactly we can write,
Example 3
Expand using the binomial theorem:
Solution:
Use the binomial theorem where and
Sometimes it is helpful to identify the pattern that results from applying the binomial theorem. Notice that powers of the variable x start at 5 and decrease to zero. The powers of the constant term start at 0 and increase to 5. The binomial coefficents can be calculated off to the side and are left to the reader as an exercise.
Answer:
The binomial may have negative terms, in which case we will obtain an alternating series.
Example 4
Expand using the binomial theorem:
Solution:
Use the binomial theorem where , , and and then simplify each term.
Answer:
Next we study the coefficients of the expansions of starting with :
Write the coefficients in a triangular array and note that each number below is the sum of the two numbers above it, always leaving a 1 on either end.

This is Pascal’s triangleA triangular array of numbers that correspond to the binomial coefficients.; it provides a quick method for calculating the binomial coefficients. Use this in conjunction with the binomial theorem to streamline the process of expanding binomials raised to powers. For example, to expand we would need two more rows of Pascal’s triangle,
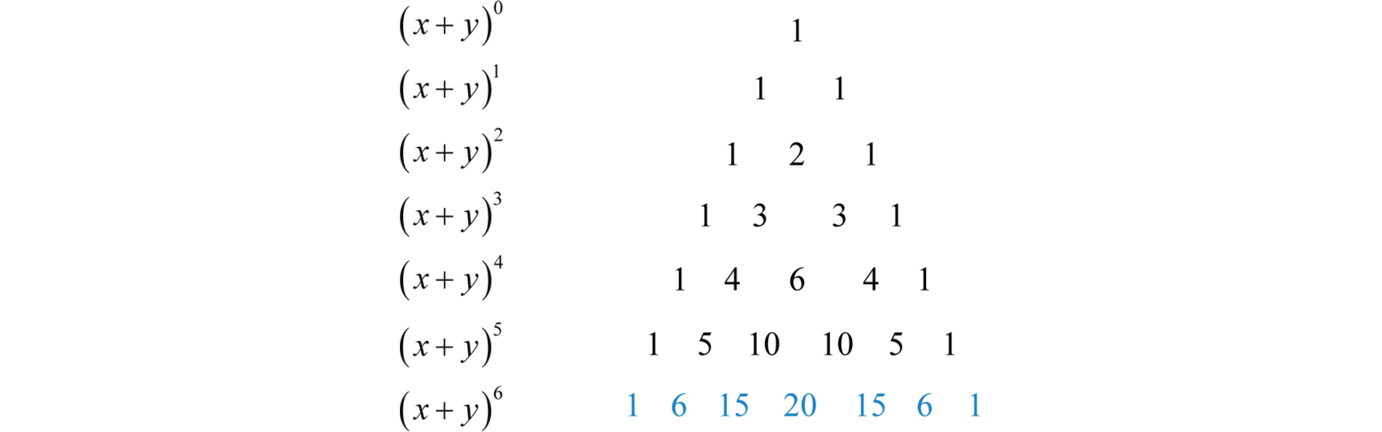
The binomial coefficients that we need are in blue. Use these numbers and the binomial theorem to quickly expand as follows:
Example 5
Expand using the binomial theorem and Pascal’s triangle:
Solution:
From Pascal’s triangle we can see that when the binomial coefficients are 1, 4, 6, 4, and 1. Use these numbers and the binomial theorem as follows:
Answer:
Key Takeaways
- To calculate the factorial of a natural number, multiply that number by all natural numbers less than it: Remember that we have defined
- The binomial coefficients are the integers calculated using the formula: .
- The binomial theorem provides a method for expanding binomials raised to powers without directly multiplying each factor: .
- Use Pascal’s triangle to quickly determine the binomial coefficients.
Topic Exercises
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
13
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Part A: Factorials and the Binomial Coefficient
Evaluate.
Rewrite using factorial notation.
Calculate the indicated binomial coefficient.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
,
-
,
-
-
-
-
-
-
Part B: Binomial Theorem
Expand using the binomial theorem.
-
Determine the factorials of the integers 5, 10, 15, 20, and 25. Which grows faster, the common exponential function or the factorial function ? Explain.
-
Research and discuss the history of the binomial theorem.
Part C: Discussion Board
Answers
-
720
-
-
3,628,800
-
-
120
-
-
17,160
-
-
15,840
-
-
-
-
- 30
- 5,040
-
-
-
-
-
-
-
-
-
-
15
-
-
21
-
-
1
-
-
1
-
-
-
-
45
-
-
1
-
-
-
-
Answer may vary
-
9.5 Review Exercises and Sample Exam
Review Exercises
-
-
-
-
-
-
-
-
-
-
-
-
-
where
-
where
-
where and
-
where and
-
1, 4, 7, 10, 13,…;
-
3, 1, −1, −3, −5,…;
-
−1, 3, −5, 7, −9,…;
-
;
-
;
-
;
-
-
-
-
-
-
Introduction to Sequences and Series
Find the first 5 terms of the sequence as well as the 30th term.
Find the first 5 terms of the sequence.
Find the indicated partial sum.
Evaluate.
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
10, 20, 30, 40, 50,…
-
−7, −5, −3, −1, 1,…
-
−2, −5, −8, −11, −14,…
-
, 0, , , 1,…
-
and
-
and
-
and
-
and
-
;
-
;
-
;
-
;
-
;
-
;
-
-
-
-
-
-
-
Find the sum of the first 175 positive odd integers.
-
Find the sum of the first 175 positive even integers.
-
Find all arithmetic means between and
-
Find all arithmetic means between and
-
A 5-year salary contract offers $58,200 for the first year with a $4,200 increase each additional year. Determine the total salary obligation over the 5-year period.
-
The first row of seating in a theater consists of 10 seats. Each successive row consists of four more seats than the previous row. If there are 14 rows, how many total seats are there in the theater?
Arithmetic Sequences and Series
Write the first 5 terms of the arithmetic sequence given its first term and common difference. Find a formula for its general term.
Given the terms of an arithmetic sequence, find a formula for the general term.
Calculate the indicated sum given the formula for the general term of an arithmetic sequence.
Evaluate.
-
;
-
;
-
;
-
;
-
;
-
;
-
4, 40, 400,…
-
−6, −30, −150,…
-
6, , ,…
-
1, , ,…
-
and
-
and
-
and
-
and
-
Find all geometric means between and
-
Find all geometric means between and
-
;
-
;
-
;
-
;
-
;
-
;
-
-
-
-
-
-
-
After the first year of operation, the value of a company van was reported to be $40,000. Because of depreciation, after the second year of operation the van was reported to have a value of $32,000 and then $25,600 after the third year of operation. Write a formula that gives the value of the van after the nth year of operation. Use it to determine the value of the van after 10 years of operation.
-
The number of cells in a culture of bacteria doubles every 6 hours. If 250 cells are initially present, write a sequence that shows the number of cells present after every 6-hour period for one day. Write a formula that gives the number of cells after the nth 6-hour period.
-
A ball bounces back to one-half of the height that it fell from. If dropped from 32 feet, approximate the total distance the ball travels.
-
A structured settlement yields an amount in dollars each year n according to the formula What is the total value of a 10-year settlement?
-
4, 9, 14,…
-
6, 18, 54,…
-
−1, , 0,…
-
10, 30, 60,…
-
0, 1, 8,…
-
−1, , ,…
-
-
-
-
-
-
-
-
-
-
-
Geometric Sequences and Series
Write the first 5 terms of the geometric sequence given its first term and common ratio. Find a formula for its general term.
Given the terms of a geometric sequence, find a formula for the general term.
Calculate the indicated sum given the formula for the general term of a geometric sequence.
Evaluate.
Classify the sequence as arithmetic, geometric, or neither.
Evaluate.
Binomial Theorem
Evaluate.
Calculate the indicated binomial coefficient.
Expand using the binomial theorem.
Answers
-
2, 7, 12, 17, 22;
-
-
−10, −20, −30, −40, −50;
-
-
−1, 0, −1, 4, −9;
-
-
3, , , , ;
-
-
-
-
-
-
0, 5, 10, 15, 20
-
-
0, −3, 9, −30, 99
-
-
35
-
-
−5
-
-
−18
-
-
−36
-
-
-
-
135
-
-
6, 11, 16, 21, 26;
-
-
5, 2, −1, −4, −7;
-
-
, , , −3, ;
-
-
7, 7, 7, 7, 7;
-
-
-
-
-
-
-
-
-
-
7,140
-
-
-
-
1,674
-
-
1,661
-
-
420
-
-
1,842
-
-
30,625
-
-
, 0,
-
-
$333,000
-
-
5, 10, 20, 40, 80;
-
-
1, , , , ;
-
-
1.2, 0.24, 0.048, 0.0096, 0.00192;
-
-
-
-
-
-
-
-
-
-
4, −16
-
-
4,095
-
-
16,383
-
-
-
-
2,516,580
-
-
−6
-
-
No sum
-
-
;
-
-
96 feet
-
-
Arithmetic;
-
-
Arithmetic;
-
-
Neither
-
-
30
-
-
−1,952
-
-
1,640
-
-
−187
-
-
84
-
-
3
-
-
39,916,800
-
-
54
-
-
-
-
56
-
-
11
-
-
-
-
-
-
-
-
-
-
-
-
-
Sample Exam
-
-
-
-
-
;
-
-
−1, , −2,…
-
1, −6, 36,…
-
, , ,…
-
, , ,…
-
10, 5, 0, −5, −10,…
-
and
-
, , −2, −8, −32,…
-
and
-
;
-
;
-
-
-
-
-
Determine the sum of the first 48 positive odd integers.
-
The first row of seating in a theater consists of 14 seats. Each successive row consists of two more seats than the previous row. If there are 22 rows, how many total seats are there in the theater?
-
A ball bounces back to one-third of the height that it fell from. If dropped from 27 feet, approximate the total distance the ball travels.
-
-
Find the first 5 terms of the sequence.
Find the indicated partial sum.
Classify the sequence as arithmetic, geometric, or neither.
Given the terms of an arithmetic sequence, find a formula for the general term.
Given the terms of a geometric sequence, find a formula for the general term.
Calculate the indicated sum.
Evaluate.
Expand using the binomial theorem.
Answers
-
−9, −3, 3, 9, 15
-
-
0, , , ,
-
-
70
-
-
Arithmetic
-
-
Geometric
-
-
-
-
-
-
−770
-
-
-
-
-
-
2,304
-
-
54 feet
-
-



