This is “Ellipses”, section 8.3 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
8.3 Ellipses
Learning Objectives
- Graph an ellipse in standard form.
- Determine the equation of an ellipse given its graph.
- Rewrite the equation of an ellipse in standard form.
The Ellipse in Standard Form
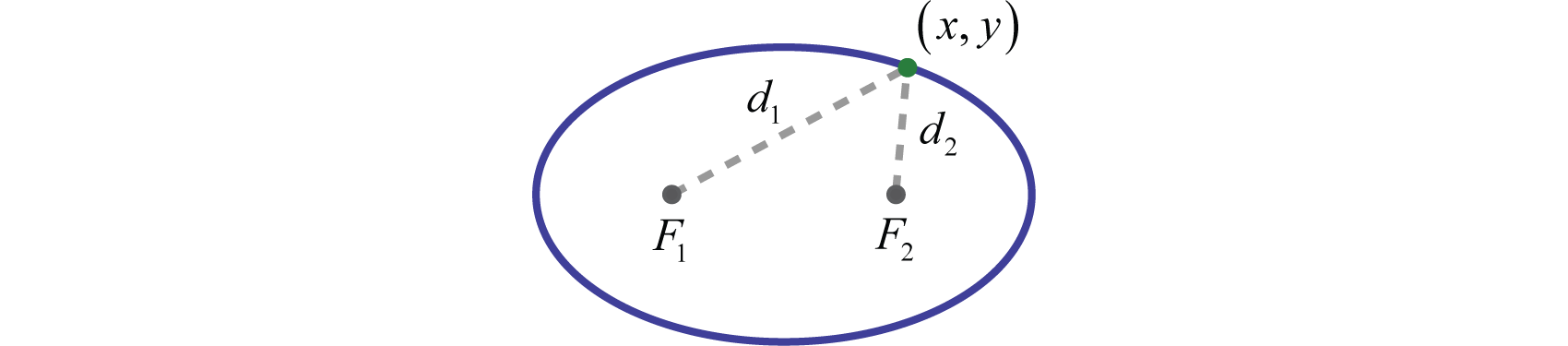
An ellipseThe set of points in a plane whose distances from two fixed points have a sum that is equal to a positive constant. is the set of points in a plane whose distances from two fixed points, called foci, have a sum that is equal to a positive constant. In other words, if points and are the foci (plural of focus) and is some given positive constant then is a point on the ellipse if as pictured below:
In addition, an ellipse can be formed by the intersection of a cone with an oblique plane that is not parallel to the side of the cone and does not intersect the base of the cone. Points on this oval shape where the distance between them is at a maximum are called verticesPoints on the ellipse that mark the endpoints of the major axis. and define the major axisThe line segment through the center of an ellipse defined by two points on the ellipse where the distance between them is a maximum.. The center of an ellipse is the midpoint between the vertices. The minor axisThe line segment through the center of an ellipse defined by two points on the ellipse where the distance between them is a minimum. is the line segment through the center of an ellipse defined by two points on the ellipse where the distance between them is at a minimum. The endpoints of the minor axis are called co-verticesPoints on the ellipse that mark the endpoints of the minor axis..
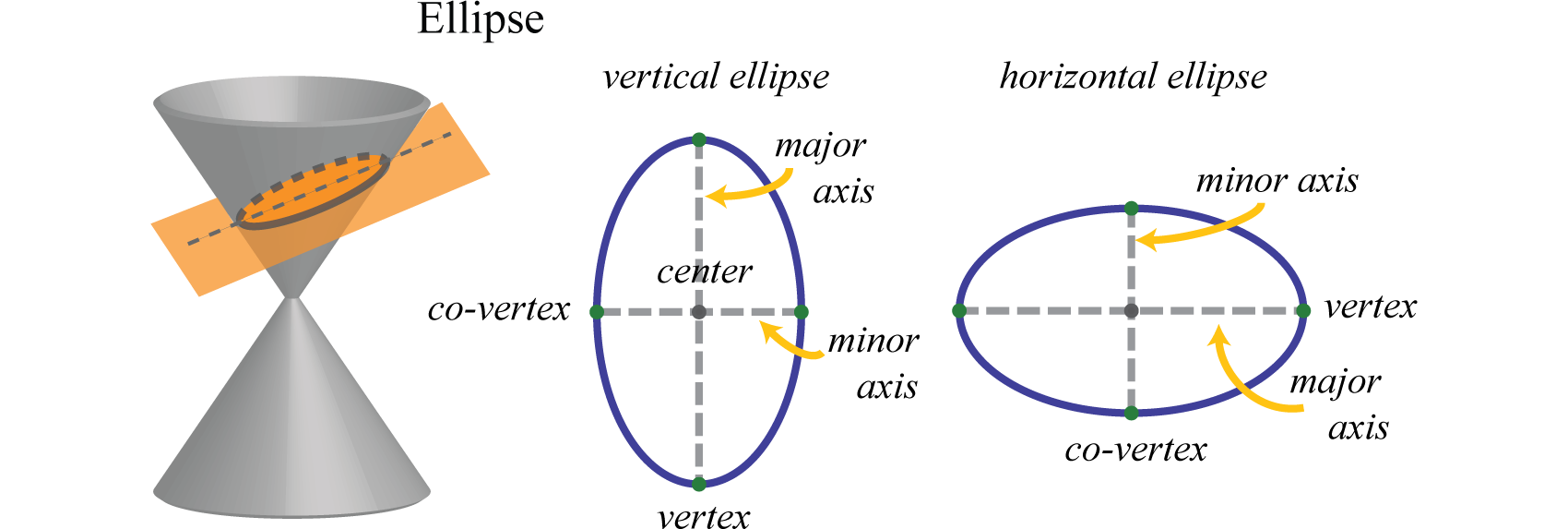
If the major axis of an ellipse is parallel to the x-axis in a rectangular coordinate plane, we say that the ellipse is horizontal. If the major axis is parallel to the y-axis, we say that the ellipse is vertical. In this section, we are only concerned with sketching these two types of ellipses. However, the ellipse has many real-world applications and further research on this rich subject is encouraged. In a rectangular coordinate plane, where the center of a horizontal ellipse is , we have
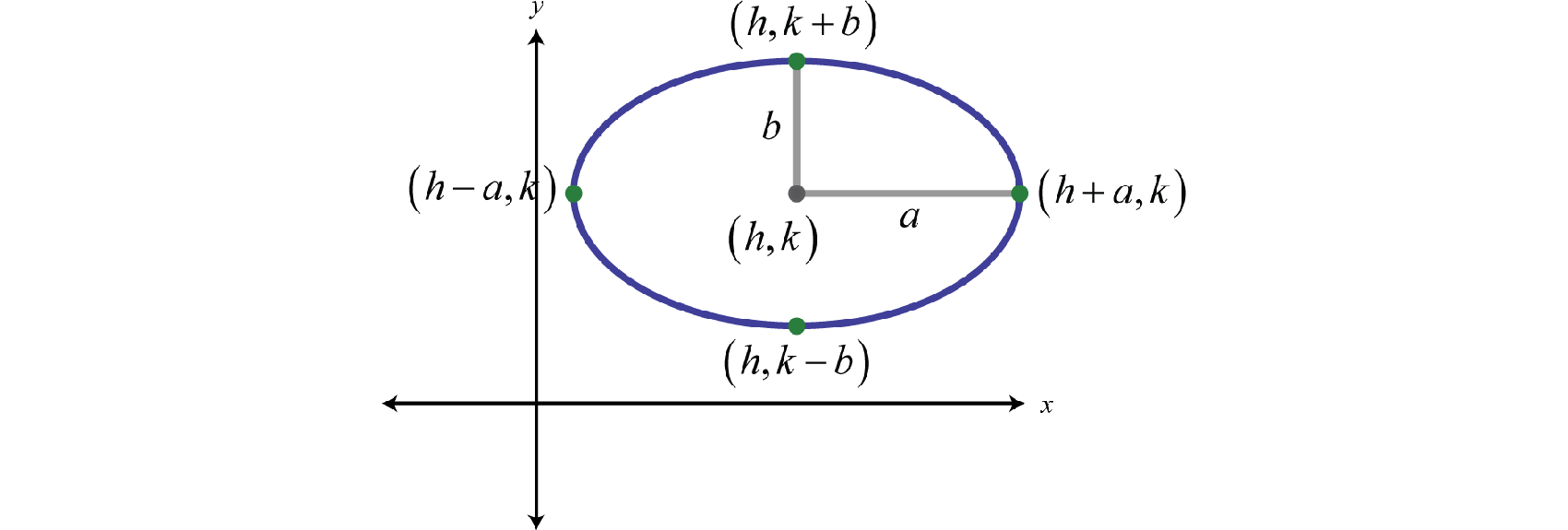
As pictured where a, one-half of the length of the major axis, is called the major radiusOne-half of the length of the major axis.. And b, one-half of the length of the minor axis, is called the minor radiusOne-half of the length of the minor axis.. The equation of an ellipse in standard formThe equation of an ellipse written in the form The center is and the larger of a and b is the major radius and the smaller is the minor radius. follows:
The vertices are and and the orientation depends on a and b. If , then the ellipse is horizontal as shown above and if , then the ellipse is vertical and b becomes the major radius. What do you think happens when ?
Equation |
Center |
a |
b |
Orientation |
|---|---|---|---|---|
Vertical |
||||
Vertical |
||||
Vertical |
||||
Horizontal |
The graph of an ellipse is completely determined by its center, orientation, major radius, and minor radius, all of which can be determined from its equation written in standard from.
Example 1
Graph:
Solution:
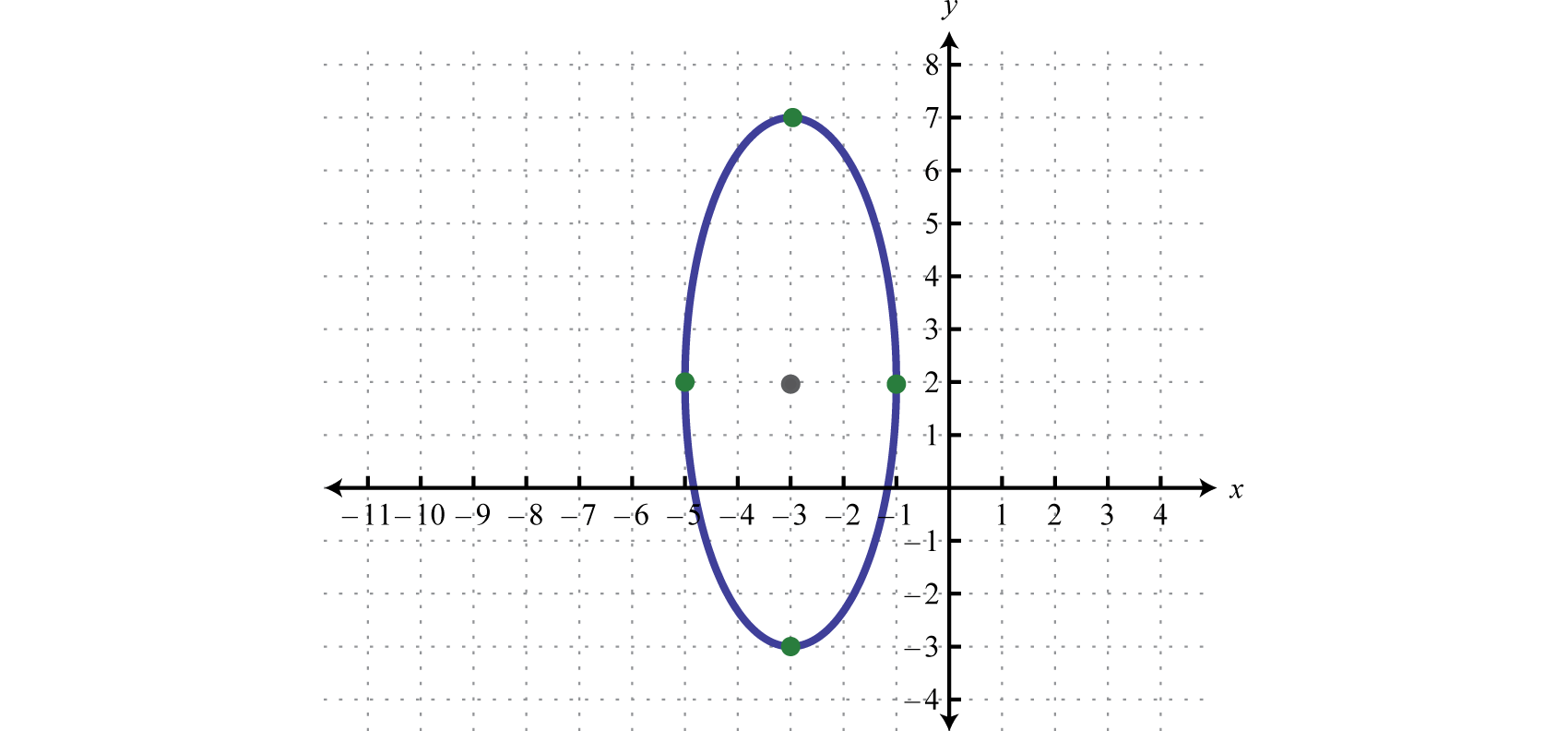
Written in this form we can see that the center of the ellipse is , , and From the center mark points 2 units to the left and right and 5 units up and down.
Then draw an ellipse through these four points.
Answer:
As with any graph, we are interested in finding the x- and y-intercepts.
Example 2
Find the intercepts:
Solution:
To find the x-intercepts set :
At this point we extract the root by applying the square root property.
Setting and solving for y leads to complex solutions, therefore, there are no y-intercepts. This is left as an exercise.
Answer: x-intercepts: ; y-intercepts: none.
Unlike a circle, standard form for an ellipse requires a 1 on one side of its equation.
Example 3
Graph and label the intercepts:
Solution:
To obtain standard form, with 1 on the right side, divide both sides by 9.
Therefore, the center of the ellipse is , , and The graph follows:
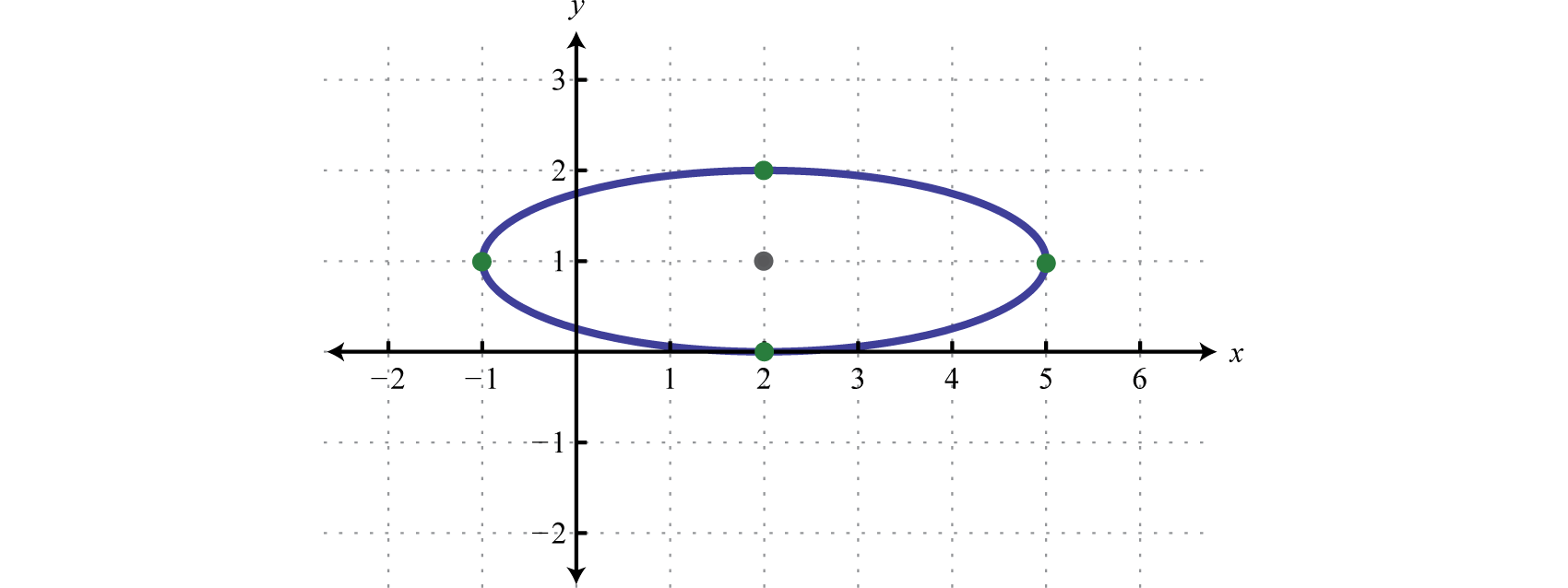
To find the intercepts we can use the standard form :
x-intercepts set |
y-intercepts set |
|---|---|
Therefore the x-intercept is and the y-intercepts are and
Answer:
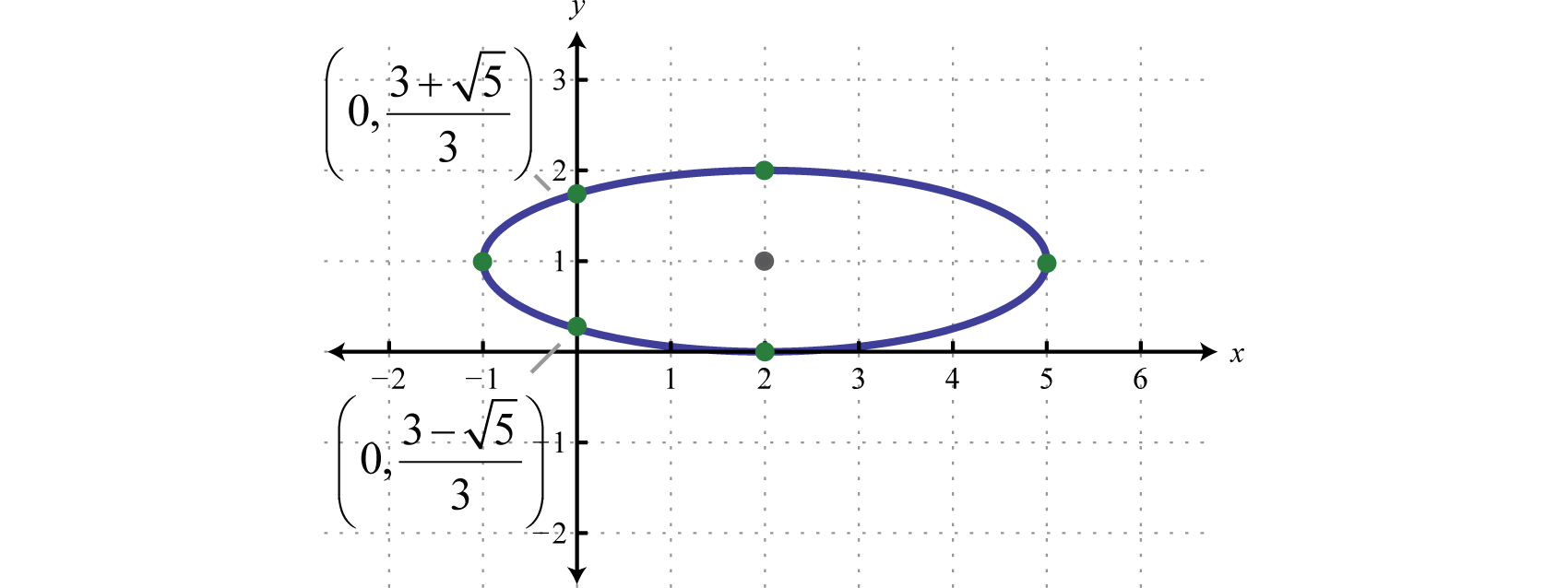
Consider the ellipse centered at the origin,
Given this equation we can write,
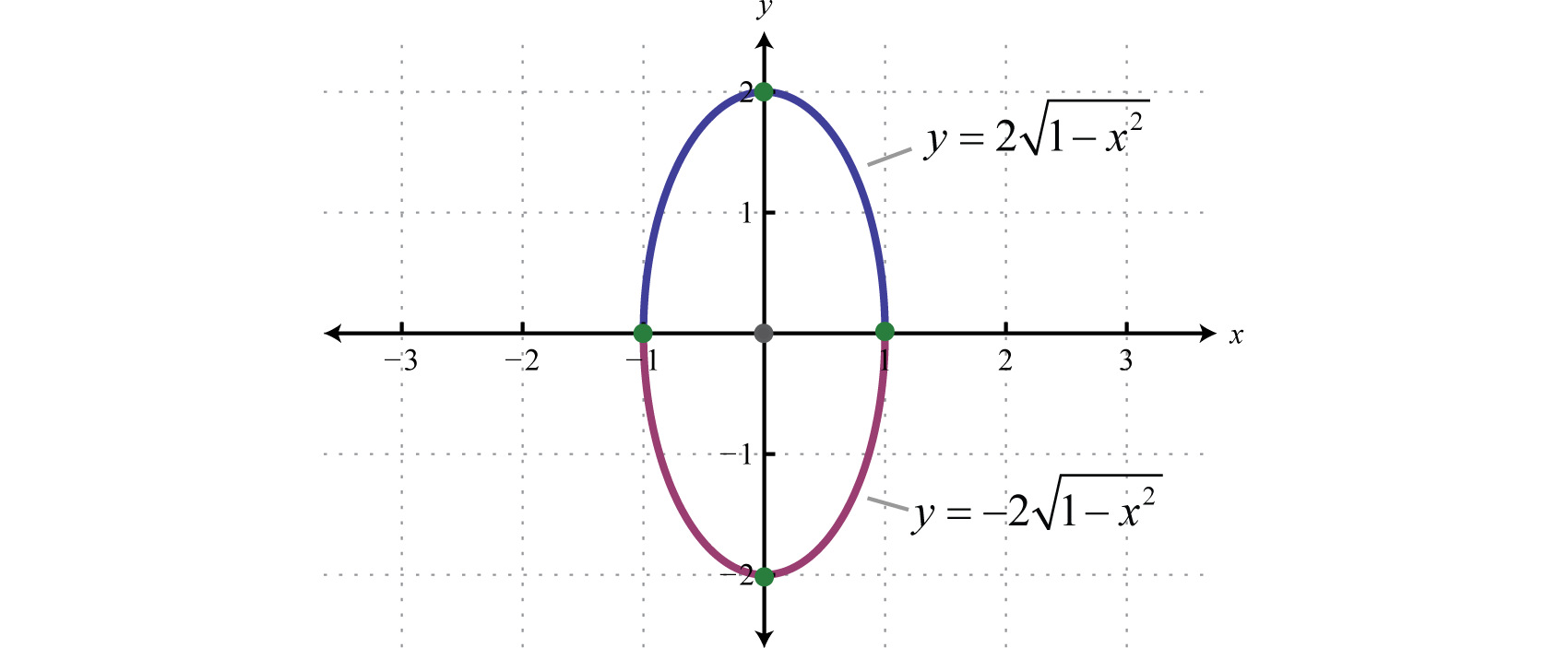
In this form, it is clear that the center is , , and Furthermore, if we solve for y we obtain two functions:
The function defined by is the top half of the ellipse and the function defined by is the bottom half.
The Ellipse in General Form
We have seen that the graph of an ellipse is completely determined by its center, orientation, major radius, and minor radius; which can be read from its equation in standard form. However, the equation is not always given in standard form. The equation of an ellipse in general formThe equation of an ellipse written in the form where follows,
where The steps for graphing an ellipse given its equation in general form are outlined in the following example.
Example 4
Graph:
Solution:
Begin by rewriting the equation in standard form.
-
Step 1: Group the terms with the same variables and move the constant to the right side. Factor so that the leading coefficient of each grouping is 1.
-
Step 2: Complete the square for each grouping. In this case, for the terms involving x use and for the terms involving y use The factor in front of the grouping affects the value used to balance the equation on the right side:
Because of the distributive property, adding 16 inside of the first grouping is equivalent to adding Similarly, adding 25 inside of the second grouping is equivalent to adding Now factor and then divide to obtain 1 on the right side.
- Step 3: Determine the center, a, and b. In this case, the center is , , and
- Step 4: Use a to mark the vertices left and right of the center, use b to mark the vertices up and down from the center, and then sketch the graph. In this case, the vertices along the minor axes are not apparent and should be labeled.
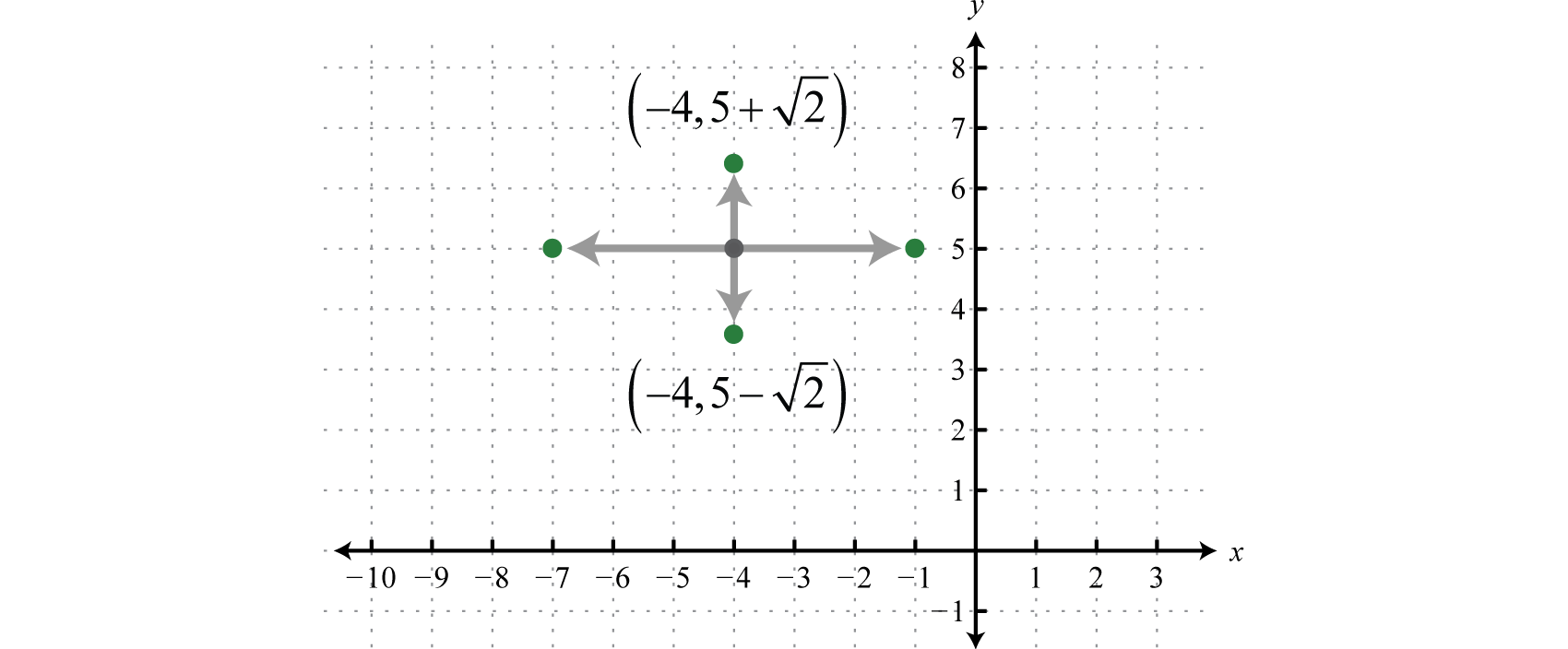
Answer:

Example 5
Determine the center of the ellipse as well as the lengths of the major and minor axes:
Solution:
In this example, we only need to complete the square for the terms involving x.
Use for the first grouping to be balanced by on the right side.
Here, the center is , , and Because b is larger than a, the length of the major axis is 2b and the length of the minor axis is 2a.
Answer: Center: ; major axis: units; minor axis: units.
Key Takeaways
- The graph of an ellipse is completely determined by its center, orientation, major radius, and minor radius.
- The center, orientation, major radius, and minor radius are apparent if the equation of an ellipse is given in standard form:
- To graph an ellipse, mark points a units left and right from the center and points b units up and down from the center. Draw an ellipse through these points.
- The orientation of an ellipse is determined by a and b. If then the ellipse is wider than it is tall and is considered to be a horizontal ellipse. If then the ellipse is taller than it is wide and is considered to be a vertical ellipse.
- If the equation of an ellipse is given in general form where , group the terms with the same variables, and complete the square for both groupings.
- We recognize the equation of an ellipse if it is quadratic in both x and y and the coefficients of each square term have the same sign.
Topic Exercises
-
-
-
-
-
-
-
Center with and
-
Center with and
-
Center with and
-
Center with and
-
Center with and
-
Center with and
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Ellipse with vertices and
-
Ellipse whose major axis has vertices and and minor axis has vertices and
-
Ellipse whose major axis has vertices and and minor axis has a length of 4 units.
-
Ellipse whose major axis has vertices and and minor axis has a length of 2 units.
Part A: The Ellipse in Standard Form
Given the equation of an ellipse in standard form, determine its center, orientation, major radius, and minor radius.
Determine the standard form for the equation of an ellipse given the following information.
Graph.
Find the x- and y-intercepts.
Find the equation of the ellipse.
Part B: The Ellipse in General Form
Rewrite in standard form and graph.
Given general form determine the intercepts.
Determine the area of the ellipse. (The area of an ellipse is given by the formula , where a and b are the lengths of the major radius and the minor radius.)
Given the graph of an ellipse, determine its equation in general form.
-
Explain why a circle can be thought of as a very special ellipse.
-
Make up your own equation of an ellipse, write it in general form and graph it.
-
Do all ellipses have intercepts? What are the possible numbers of intercepts for an ellipse? Explain.
-
Research and discuss real-world examples of ellipses.
Part C: Discussion Board
Answers
-
Center: ; orientation: vertical; major radius: 7 units; minor radius: 2 units; ;
-
-
Center: ; orientation: horizontal; major radius: units; minor radius: 1 unit; ;
-
-
Center: ; orientation: horizontal; major radius: 3 units; minor radius: 2 units; ;
-
-
-
-
-
-
-
-
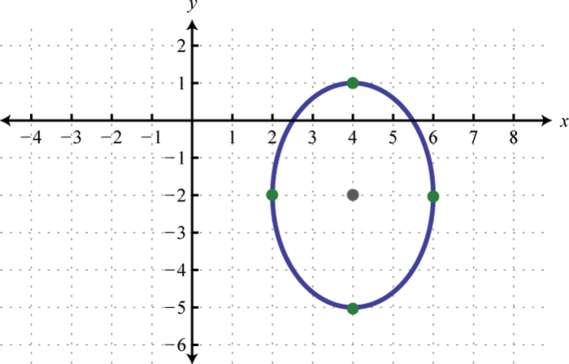
-
-
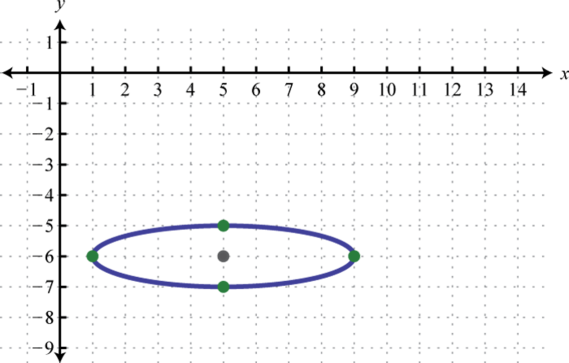
-
-

-
-
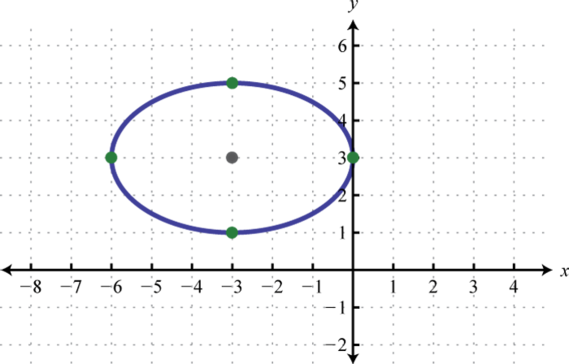
-
-

-
-
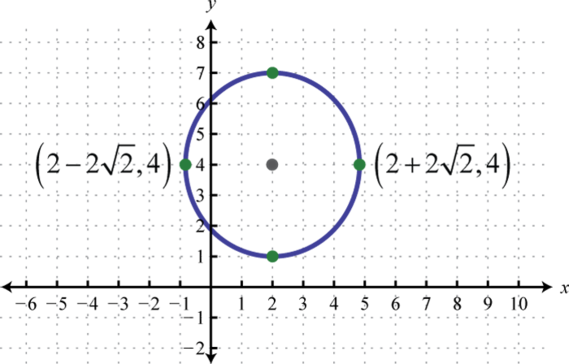
-
-
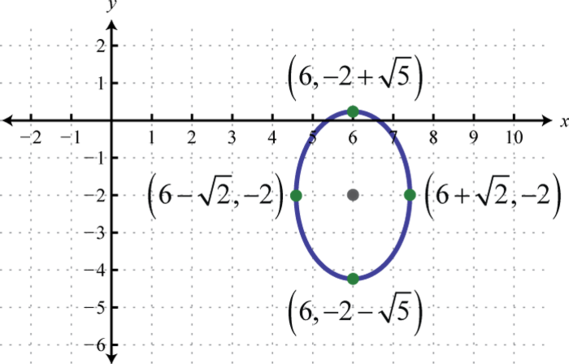
-
-

-
-
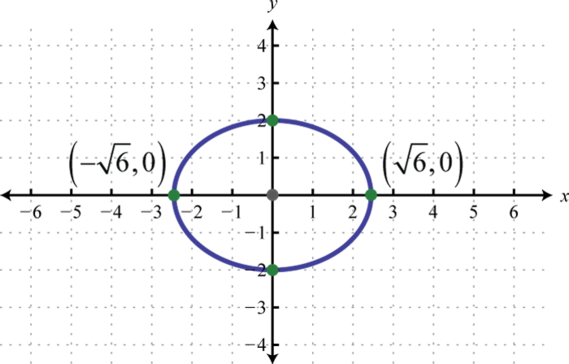
-
-
x-intercepts: ; y-intercepts: none
-
-
x-intercepts: ; y-intercepts:
-
-
x-intercepts: none; y-intercepts:
-
-
x-intercepts: ; y-intercepts:
-
-
-
-
-
-
;
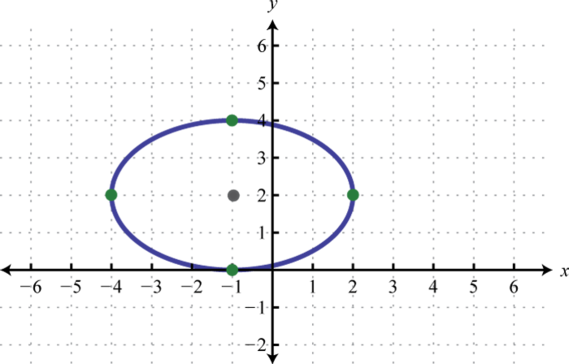
-
-
;
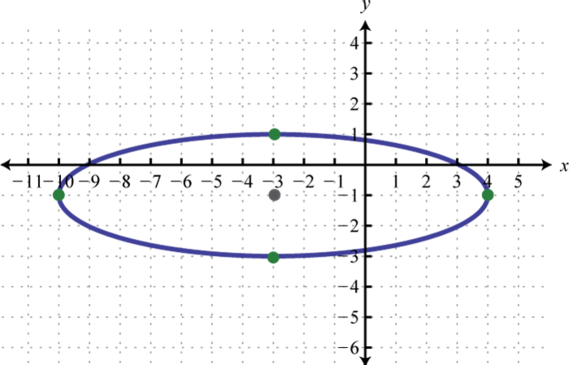
-
-
;
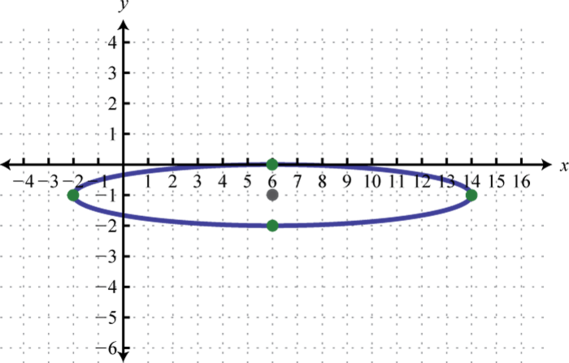
-
-
;
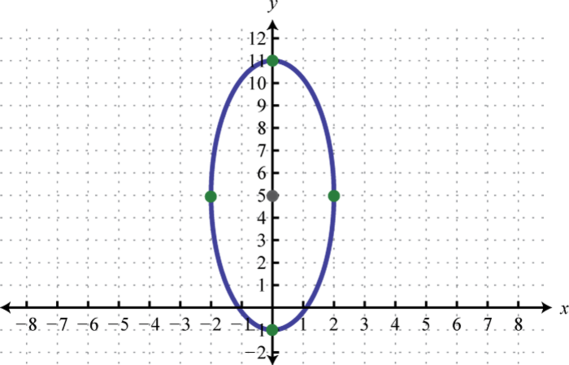
-
-
;
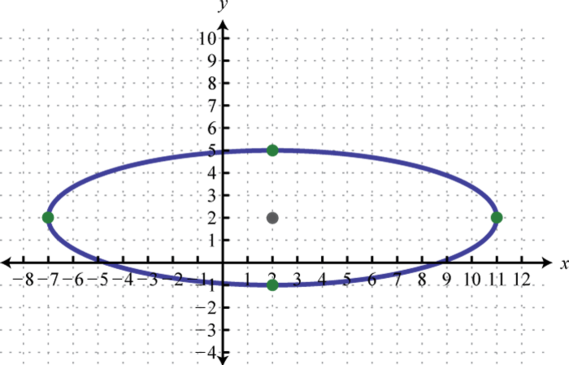
-
-
;
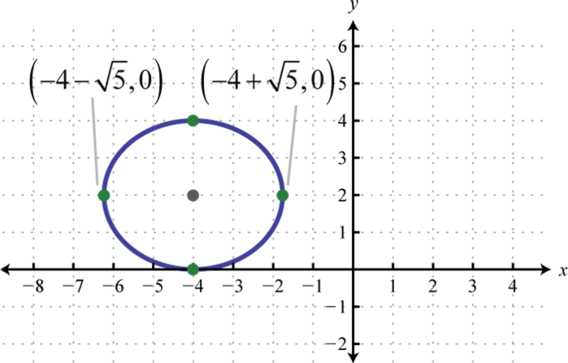
-
-
;

-
-
;
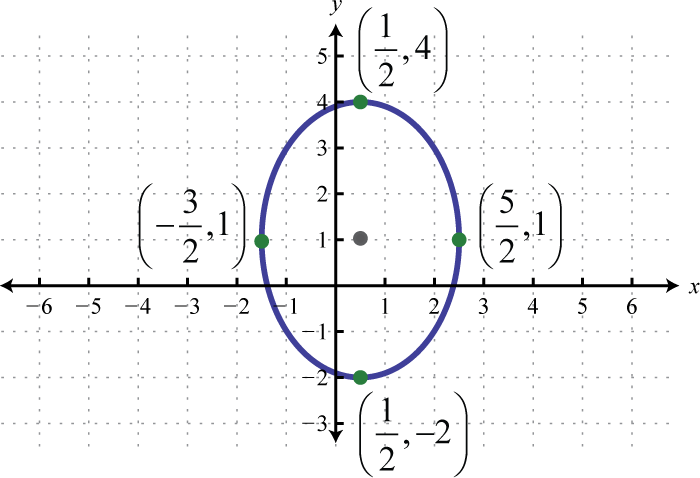
-
-
;

-
-
x-intercepts: none; y-intercepts:
-
-
x-intercepts: ; y-intercepts:
-
-
x-intercepts: ; y-intercepts: none
-
-
square units
-
-
square units
-
-
-
-
-
-
Answer may vary
-
-
Answer may vary
-