This is “Solving Equations and Inequalities”, chapter 6 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
Chapter 6 Solving Equations and Inequalities
6.1 Extracting Square Roots and Completing the Square
Learning Objectives
- Solve certain quadratic equations by extracting square roots.
- Solve any quadratic equation by completing the square.
Extracting Square Roots
Recall that a quadratic equation is in standard formAny quadratic equation in the form , where a, b, and c are real numbers and if it is equal to 0:
where a, b, and c are real numbers and A solution to such an equation is a root of the quadratic function defined by Quadratic equations can have two real solutions, one real solution, or no real solution—in which case there will be two complex solutions. If the quadratic expression factors, then we can solve the equation by factoring. For example, we can solve by factoring as follows:
The two solutions are Here we use ± to write the two solutions in a more compact form. The goal in this section is to develop an alternative method that can be used to easily solve equations where , giving the form
The equation is in this form and can be solved by first isolating
If we take the square root of both sides of this equation, we obtain the following:
Here we see that are solutions to the resulting equation. In general, this describes the square root propertyFor any real number k, if , then ; for any real number k,
Applying the square root property as a means of solving a quadratic equation is called extracting the rootApplying the square root property as a means of solving a quadratic equation.. This method allows us to solve equations that do not factor.
Example 1
Solve:
Solution:
Notice that the quadratic expression on the left does not factor. However, it is in the form and so we can solve it by extracting the roots. Begin by isolating
Next, apply the square root property. Remember to include the ± and simplify.
For completeness, check that these two real solutions solve the original quadratic equation.
Answer: Two real solutions,
Sometimes quadratic equations have no real solution. In this case, the solutions will be complex numbers.
Example 2
Solve:
Solution:
Begin by isolating and then apply the square root property.
After applying the square root property, we are left with the square root of a negative number. Therefore, there is no real solution to this equation; the solutions are complex. We can write these solutions in terms of the imaginary unit
Answer: Two complex solutions,
Consider solving the following equation:
To solve this equation by factoring, first square and then put the equation in standard form, equal to zero, by subtracting 9 from both sides.
Factor and then apply the zero-product property.
The two solutions are −8 and −2. When an equation is in this form, we can obtain the solutions in fewer steps by extracting the roots.
Example 3
Solve by extracting roots:
Solution:
The term with the square factor is isolated so we begin by applying the square root property.
At this point, separate the “plus or minus” into two equations and solve each individually.
Answer: The solutions are −2 and −8.
In addition to fewer steps, this method allows us to solve equations that do not factor.
Example 4
Solve:
Solution:
Begin by isolating the term with the square factor.
Next, extract the roots, solve for x, and then simplify.
Answer: The solutions are and
Completing the Square
In this section, we will devise a method for rewriting any quadratic equation of the form
as an equation of the form
This process is called completing the squareThe process of rewriting a quadratic equation to be in the form . As we have seen, quadratic equations in this form can be easily solved by extracting roots. We begin by examining perfect square trinomials:
The last term, 9, is the square of one-half of the coefficient of x. In general, this is true for any perfect square trinomial of the form
In other words, any trinomial of the form will be a perfect square trinomial if
Note: It is important to point out that the leading coefficient must be equal to 1 for this to be true.
Example 5
Complete the square:
Solution:
In this example, the coefficient b of the middle term is −6. Find the value that completes the square as follows:
The value that completes the square is 9.
Answer:
Example 6
Complete the square:
Solution:
Here b = 1. Find the value that will complete the square as follows:
The value completes the square:
Answer:
We can use this technique to solve quadratic equations. The idea is to take any quadratic equation in standard form and complete the square so that we can solve it by extracting roots. The following are general steps for solving a quadratic equation with leading coefficient 1 in standard form by completing the square.
Example 7
Solve by completing the square:
Solution:
It is important to notice that the leading coefficient is 1.
Step 1: Add or subtract the constant term to obtain an equation of the form Here we add 2 to both sides of the equation.
Step 2: Use to determine the value that completes the square. In this case, b = −8:
Step 3: Add to both sides of the equation and complete the square.
Step 4: Solve by extracting roots.
Answer: The solutions are and The check is left to the reader.
Example 8
Solve by completing the square:
Solution:
Begin by adding 48 to both sides.
Next, find the value that completes the square using b = 2.
To complete the square, add 1 to both sides, complete the square, and then solve by extracting the roots.
At this point, separate the “plus or minus” into two equations and solve each individually.
Answer: The solutions are −8 and 6.
Note: In the previous example the solutions are integers. If this is the case, then the original equation will factor.
If an equation factors, we can solve it by factoring. However, not all quadratic equations will factor. Furthermore, equations often have complex solutions.
Example 9
Solve by completing the square:
Solution:
Begin by subtracting 26 from both sides of the equation.
Here b = −10, and we determine the value that completes the square as follows:
To complete the square, add 25 to both sides of the equation.
Factor and then solve by extracting roots.
Answer: The solutions are
The coefficient of x is not always divisible by 2.
Example 10
Solve by completing the square:
Solution:
Begin by subtracting 4 from both sides.
Use b = 3 to find the value that completes the square:
To complete the square, add to both sides of the equation.
Solve by extracting roots.
Answer: The solutions are
So far, all of the examples have had a leading coefficient of 1. The formula determines the value that completes the square only if the leading coefficient is 1. If this is not the case, then simply divide both sides by the leading coefficient before beginning the steps outlined for completing the square.
Example 11
Solve by completing the square:
Solution:
Notice that the leading coefficient is 2. Therefore, divide both sides by 2 before beginning the steps required to solve by completing the square.
Add to both sides of the equation.
Here , and we can find the value that completes the square as follows:
To complete the square, add to both sides of the equation.
Next, solve by extracting roots.
Answer: The solutions are
Key Takeaways
- Solve equations of the form by extracting the roots.
- Extracting roots involves isolating the square and then applying the square root property. Remember to include “±” when taking the square root of both sides.
- After applying the square root property, solve each of the resulting equations. Be sure to simplify all radical expressions and rationalize the denominator if necessary.
- Solve any quadratic equation by completing the square.
- You can apply the square root property to solve an equation if you can first convert the equation to the form
- To complete the square, first make sure the equation is in the form The leading coefficient must be 1. Then add the value to both sides and factor.
- The process for completing the square always works, but it may lead to some tedious calculations with fractions. This is the case when the middle term, b, is not divisible by 2.
Topic Exercises
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Solve for x: ,
-
Solve for x: ,
-
The diagonal of a square measures 3 centimeters. Find the length of each side.
-
The length of a rectangle is twice its width. If the diagonal of the rectangle measures 10 meters, then find the dimensions of the rectangle.
-
If a circle has an area of square centimeters, then find its radius.
-
If a square has an area of 27 square centimeters, then find the length of each side.
-
The height in feet of an object dropped from an 18-foot stepladder is given by , where t represents the time in seconds after the object is dropped. How long does it take the object to hit the ground? (Hint: The height is 0 when the object hits the ground. Round to the nearest hundredth of a second.)
-
The height in feet of an object dropped from a 50-foot platform is given by , where t represents the time in seconds after the object is dropped. How long does it take the object to hit the ground? (Round to the nearest hundredth of a second.)
-
How high does a 22-foot ladder reach if its base is 6 feet from the building on which it leans? Round to the nearest tenth of a foot.
-
The height of a triangle is the length of its base. If the area of the triangle is 72 square meters, find the exact length of the triangle’s base.
Part A: Extracting Square Roots
Solve by factoring and then solve by extracting roots. Check answers.
Solve by extracting the roots.
Part B: Completing the Square
Complete the square.
Solve by factoring and then solve by completing the square. Check answers.
Solve by completing the square.
Solve by completing the square and round the solutions to the nearest hundredth.
-
Create an equation of your own that can be solved by extracting the roots. Share it, along with the solution, on the discussion board.
-
Explain why the technique of extracting roots greatly expands our ability to solve quadratic equations.
-
Explain why the technique for completing the square described in this section requires that the leading coefficient be equal to 1.
-
Derive a formula for the diagonal of a square in terms of its sides.
Part C: Discussion Board
Answers
-
−4, 4
-
-
-
-
1, 3
-
-
-
-
0, 10
-
-
±9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
−9, −5
-
-
-
-
-
-
-
-
-
-
-
-
−1, 3
-
-
-
-
centimeters
-
-
centimeters
-
-
1.06 seconds
-
-
21.2 feet
-
-
-
-
-
-
-
-
-
-
-
-
−4, 2
-
-
−6, 4
-
-
−7, 4
-
-
-
-
-
-
-
-
-
-
-
-
−15, 5
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
0.19, 1.31
-
-
−0.45, 1.12
-
-
0.33, 0.67
-
-
Answer may vary
-
-
Answer may vary
-
6.2 Quadratic Formula
Learning Objectives
- Solve quadratic equations using the quadratic formula.
- Use the determinant to determine the number and type of solutions to a quadratic equation.
The Quadratic Formula
In this section, we will develop a formula that gives the solutions to any quadratic equation in standard form. To do this, we begin with a general quadratic equation in standard form and solve for x by completing the square. Here a, b, and c are real numbers and :
Determine the constant that completes the square: take the coefficient of x, divide it by 2, and then square it.
Add this to both sides of the equation to complete the square and then factor.
Solve by extracting roots.
This derivation gives us a formula that solves any quadratic equation in standard form. Given , where a, b, and c are real numbers and , the solutions can be calculated using the quadratic formulaThe formula , which gives the solutions to any quadratic equation in the standard form , where a, b, and c are real numbers and :
Example 1
Solve using the quadratic formula:
Solution:
Begin by identifying the coefficients of each term: a, b, and c.
Substitute these values into the quadratic formula and then simplify.
Separate the “plus or minus” into two equations and simplify further.
Answer: The solutions are and 5.
The previous example can be solved by factoring as follows:
Of course, if the quadratic expression factors, then it is a best practice to solve the equation by factoring. However, not all quadratic polynomials factor so easily. The quadratic formula provides us with a means to solve all quadratic equations.
Example 2
Solve using the quadratic formula:
Solution:
Begin by identifying a, b, and c.
Substitute these values into the quadratic formula.
At this point we see that and thus the fraction can be simplified further.
It is important to point out that there are two solutions here:
We may use ± to write the two solutions in a more compact form.
Answer: The solutions are
Sometimes terms are missing. When this is the case, use 0 as the coefficient.
Example 3
Solve using the quadratic formula:
Solution:
This equation is equivalent to
And we can use the following coefficients:
Substitute these values into the quadratic formula.
Since the coefficient of x was 0, we could have solved this equation by extracting the roots. As an exercise, solve it using this method and verify that the results are the same.
Answer: The solutions are
Often solutions to quadratic equations are not real.
Example 4
Solve using the quadratic formula:
Solution:
Begin by identifying a, b, and c. Here
Substitute these values into the quadratic formula and then simplify.
Check these solutions by substituting them into the original equation.
Answer: The solutions are
The equation may not be given in standard form. The general steps for using the quadratic formula are outlined in the following example.
Example 5
Solve:
Solution:
Step 1: Write the quadratic equation in standard form, with zero on one side of the equal sign.
Step 2: Identify a, b, and c for use in the quadratic formula. Here
Step 3: Substitute the appropriate values into the quadratic formula and then simplify.
Answer: The solution is
The Discriminant
If given a quadratic equation in standard form, , where a, b, and c are real numbers and , then the solutions can be calculated using the quadratic formula:
As we have seen, the solutions can be rational, irrational, or complex. We can determine the number and type of solutions by studying the discriminantThe expression inside the radical of the quadratic formula, , the expression inside the radical, If the value of this expression is negative, then the equation has two complex solutions. If the discriminant is positive, then the equation has two real solutions. And if the discriminant is 0, then the equation has one real solution, a double root.
Example 6
Determine the type and number of solutions:
Solution:
We begin by identifying a, b, and c. Here
Substitute these values into the discriminant and simplify.
Since the discriminant is negative, we conclude that there are no real solutions. They are complex.
Answer: Two complex solutions.
If we use the quadratic formula in the previous example, we find that a negative radicand introduces the imaginary unit and we are left with two complex solutions.
Note: Irrational and complex solutions of quadratic equations always appear in conjugate pairs.
Example 7
Determine the type and number of solutions:
Solution:
In this example,
Substitute these values into the discriminant and simplify.
Since the discriminant is positive, we conclude that the equation has two real solutions. Furthermore, since the discriminant is a perfect square, we obtain two rational solutions.
Answer: Two rational solutions
Because the discriminant is a perfect square, we could solve the previous quadratic equation by factoring or by using the quadratic formula.
| Solve by factoring: | Solve using the quadratic formula: |
|---|---|
Given the special condition where the discriminant is 0, we obtain only one solution, a double root.
Example 8
Determine the type and number of solutions:
Solution:
Here , , and , and we have
Since the discriminant is 0, we conclude that the equation has only one real solution, a double root.
Answer: One rational solution
Since 0 is a perfect square, we can solve the equation above by factoring.
Here is a solution that occurs twice; it is a double root.
Example 9
Determine the type and number of solutions:
Solution:
Here , , and , and we have
Since the discriminant is positive, we can conclude that the equation has two real solutions. Furthermore, since 20 is not a perfect square, both solutions are irrational.
Answer: Two irrational solutions.
If we use the quadratic formula in the previous example, we find that a positive radicand in the quadratic formula leads to two real solutions.
The two real solutions are and Note that these solutions are irrational; we can approximate the values on a calculator.
In summary, if given any quadratic equation in standard form, , where a, b, and c are real numbers and , then we have the following:
Furthermore, if the discriminant is nonnegative and a perfect square, then the solutions to the equation are rational; otherwise they are irrational. As we will see, knowing the number and type of solutions ahead of time helps us determine which method is best for solving a quadratic equation.
Try this! Determine the number and type of solutions:
Answer: Two complex solutions.
Key Takeaways
- We can use the quadratic formula to solve any quadratic equation in standard form.
- To solve any quadratic equation, we first rewrite it in standard form , substitute the appropriate coefficients into the quadratic formula, , and then simplify.
- We can determine the number and type of solutions to any quadratic equation in standard form using the discriminant, If the value of this expression is negative, then the equation has two complex solutions. If the discriminant is positive, then the equation has two real solutions. And if the discriminant is 0, then the equation has one real solution, a double root.
- We can further classify real solutions into rational or irrational numbers. If the discriminant is a perfect square, the roots are rational and the equation will factor. If the discriminant is not a perfect square, the roots are irrational.
Topic Exercises
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
The height in feet reached by a baseball tossed upward at a speed of 48 feet per second from the ground is given by , where t represents time in seconds after the ball is tossed. At what time does the baseball reach 24 feet? (Round to the nearest tenth of a second.)
-
The height in feet of a projectile launched upward at a speed of 32 feet per second from a height of 64 feet is given by At what time after launch does the projectile hit the ground? (Round to the nearest tenth of a second.)
-
The profit in dollars of running an assembly line that produces custom uniforms each day is given by where t represents the number of hours the line is in operation. Determine the number of hours the assembly line should run in order to make a profit of $1,760 per day.
-
A manufacturing company has determined that the daily revenue R in thousands of dollars is given by where n represents the number of pallets of product sold. Determine the number of pallets that must be sold in order to maintain revenues at 60 thousand dollars per day.
-
The area of a rectangle is 10 square inches. If the length is 3 inches more than twice the width, then find the dimensions of the rectangle. (Round to the nearest hundredth of an inch.)
-
The area of a triangle is 2 square meters. If the base is 2 meters less than the height, then find the base and the height. (Round to the nearest hundredth of a meter.)
-
To safely use a ladder, the base should be placed about of the ladder’s length away from the wall. If a 32-foot ladder is used safely, then how high against a building does the top of the ladder reach? (Round to the nearest tenth of a foot.)
-
The length of a rectangle is twice its width. If the diagonal of the rectangle measures 10 centimeters, then find the dimensions of the rectangle. (Round to the nearest tenth of a centimeter.)
-
Assuming dry road conditions and average reaction times, the safe stopping distance in feet of a certain car is given by where x represents the speed of the car in miles per hour. Determine the safe speed of the car if you expect to stop in 50 feet. (Round to the nearest mile per hour.)
-
The width of a rectangular solid is 2.2 centimeters less than its length and the depth measures 10 centimeters.

Determine the length and width if the total volume of the solid is 268.8 cubic centimeters.
-
An executive traveled 25 miles in a car and then another 30 miles on a helicopter. If the helicopter was 10 miles per hour less than twice as fast as the car and the total trip took 1 hour, then what was the average speed of the car? (Round to the nearest mile per hour.)
-
Joe can paint a typical room in 1.5 hours less time than James. If Joe and James can paint 2 rooms working together in an 8-hour shift, then how long does it take James to paint a single room? (Round to the nearest tenth of an hour.)
Part A: The Quadratic Formula
Identify the coefficients, a, b and c, used in the quadratic formula. Do not solve.
Solve by factoring and then solve using the quadratic formula. Check answers.
Solve by extracting the roots and then solve using the quadratic formula. Check answers.
Solve using the quadratic formula.
Assume p and q are nonzero integers and use the quadratic formula to solve for x.
Solve using algebra.
Part B: The Discriminant
Calculate the discriminant and use it to determine the number and type of solutions. Do not solve.
Find a nonzero integer p so that the following equations have one real solution. (Hint: If the discriminant is zero, then there will be one real solution.)
-
When talking about a quadratic equation in standard form , why is it necessary to state that ? What would happen if a is equal to zero?
-
Research and discuss the history of the quadratic formula and solutions to quadratic equations.
-
Solve for x by completing the square.
Part C: Discussion Board
Answers
-
; ;
-
-
; ;
-
-
; ;
-
-
; ;
-
-
; ;
-
-
−2, 8
-
-
-
-
-
-
-
-
4, 5
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
or
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
0.6 seconds and 2.4 seconds
-
-
12 hours
-
-
Length: 6.22 inches; width: 1.61 inches
-
-
31.0 feet
-
-
23 miles per hour
-
-
42 miles per hour
-
-
−3; two complex solutions
-
-
16; two rational solutions
-
-
25; two rational solutions
-
-
−72; two complex solutions
-
-
9; two rational solutions
-
-
−1; two complex solutions
-
-
25; two rational solutions
-
-
0; one rational solution
-
-
-
-
-
-
Answer may vary
-
-
Answer may vary
6.3 Solving Equations Quadratic in Form
Learning Objectives
- Develop a general strategy for solving quadratic equations.
- Solve equations that are quadratic in form.
General Guidelines for Solving Quadratic Equations
Use the coefficients of a quadratic equation to help decide which method is most appropriate for solving it. While the quadratic formula always works, it is sometimes not the most efficient method. If given any quadratic equation in standard form,
where c = 0, then it is best to factor out the GCF and solve by factoring.
Example 1
Solve:
Solution:
In this case, c = 0 and we can solve by factoring out the GCF 3x.
Then apply the zero-product property and set each factor equal to zero.
Answer: The solutions are 0 and
If b = 0, then we can solve by extracting the roots.
Example 2
Solve:
Solution:
In this case, b = 0 and we can solve by extracting the roots. Begin by isolating the square.
Next, apply the square root property. Remember to include the ±.
Answer: The solutions are
When given a quadratic equation in standard form where a, b, and c are all nonzero, determine the value for the discriminant using the formula
- If the discriminant is a perfect square, then solve by factoring.
- If the discriminant is not a perfect square, then solve using the quadratic formula.
Recall that if the discriminant is not a perfect square and positive, the quadratic equation will have two irrational solutions. And if the discriminant is negative, the quadratic equation will have two complex conjugate solutions.
Example 3
Solve:
Solution:
Begin by rewriting the quadratic equation in standard form.
Substitute a = 9, b = 30, and c = 25 into the discriminant formula.
Since the discriminant is 0, solve by factoring and expect one real solution, a double root.
Answer: The solution is
It is good to know that the quadratic formula will work to find the solutions to all of the examples in this section. However, it is not always the best solution. If the equation can be solved by factoring or by extracting the roots, you should use that method.
Solving Equations Quadratic in Form
In this section we outline an algebraic technique that is used extensively in mathematics to transform equations into familiar forms. We begin by defining quadratic formAn equation of the form where a, b and c are real numbers and u represents an algebraic expression.,
Here u represents an algebraic expression. Some examples follow:
If we can express an equation in quadratic form, then we can use any of the techniques used to solve quadratic equations. For example, consider the following fourth-degree polynomial equation,
If we let then and we can write
This substitution transforms the equation into a familiar quadratic equation in terms of u which, in this case, can be solved by factoring.
Since we can back substitute and then solve for x.
Therefore, the equation has four solutions , two real and two complex. This technique, often called a u-substitutionA technique in algebra using substitution to transform equations into familiar forms., can also be used to solve some non-polynomial equations.
Example 4
Solve:
Solution:
This is a radical equation that can be written in quadratic form. If we let then and we can write
Solve for u.
Back substitute and solve for x.
Recall that squaring both sides of an equation introduces the possibility of extraneous solutions. Therefore we must check our potential solutions.
Because is extraneous, there is only one solution,
Answer: The solution is 16.
Example 5
Solve:
Solution:
If we let , then and we can write
Solve for u.
Back substitute and solve for x.
Check.
Answer: The solutions are −8, 125.
Example 6
Solve:
Solution:
If we let , then and we can write
Solve for u.
Back substitute and solve for y.
The original equation is actually a rational equation where In this case, the solutions are not restrictions; they solve the original equation.
Answer: The solutions are
Example 7
Solve:
Solution:
If we let , then and we can write
Solve for u.
Back substitute and solve for t.
Answer: The solutions are −1, The check is left to the reader.
So far all of the examples were of equations that factor. As we know, not all quadratic equations factor. If this is the case, we use the quadratic formula.
Example 8
Solve: Approximate to the nearest hundredth.
Solution:
If we let , then and we can write
This equation does not factor; therefore, use the quadratic formula to find the solutions for u. Here , , and
Therefore, Now back substitute and solve for x.
Round the four solutions as follows.
Answer: The solutions are approximately ±1.89, ±2.53.
If multiple roots and complex roots are counted, then the fundamental theorem of algebraIf multiple roots and complex roots are counted, then every polynomial with one variable will have as many roots as its degree. implies that every polynomial with one variable will have as many roots as its degree. For example, we expect to have three roots. In other words, the equation
should have three solutions. To find them one might first think of trying to extract the cube roots just as we did with square roots,
As you can see, this leads to one solution, the real cube root. There should be two others; let’s try to find them.
Example 9
Find the set of all roots:
Solution:
Notice that the expression is a difference of cubes and recall that Here and and we can write
Next apply the zero-product property and set each factor equal to zero. After setting the factors equal to zero we can then solve the resulting equation using the appropriate methods.
Using this method we were able to obtain the set of all three roots , one real and two complex.
Answer:
Sometimes the roots of a function will occur multiple times. For example, has degree three where the roots can be found as follows:
Even though g is of degree 3 there is only one real root {2}; it occurs 3 times.
Key Takeaways
- The quadratic formula can solve any quadratic equation. However, it is sometimes not the most efficient method.
- If a quadratic equation can be solved by factoring or by extracting square roots you should use that method.
- We can sometimes transform equations into equations that are quadratic in form by making an appropriate u-substitution. After solving the equivalent equation, back substitute and solve for the original variable.
- Counting multiple and complex roots, the fundamental theorem of algebra guarantees as many roots as the degree of a polynomial equation with one variable.
Topic Exercises
Part A: Solving Quadratic Equations
Solve.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
,
-
,
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Part B: Solving Equations Quadratic in Form
Find all solutions.
Find all solutions. Round your answers to the nearest hundredth.
Find the set of all roots.
Find all solutions.
Find a quadratic function with integer coefficients and the given set of roots. (Hint: If and are roots, then )
-
On a note card, write out your strategy for solving a quadratic equation. Share your strategy on the discussion board.
-
Make up your own equation that is quadratic in form. Share it and the solution on the discussion board.
Part C: Discussion Board
Answers
-
0, 9
-
-
, 0
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
,
-
-
±2, ±3
-
-
1
-
-
4, 9
-
-
−27, −8
-
-
-
-
, 5
-
-
-
-
-
-
-
-
-
-
0,
-
-
-
-
, 6
-
-
1, 16
-
-
−1,
-
-
,
-
-
−2, 1
-
-
, 16
-
-
, 1
-
-
±1.26, ±2.10
-
-
±1.61, ±2.33
-
-
±1.06, ±1.69
-
-
-
-
-
-
-
-
-
-
-
-
−2, 1, ,
-
-
−3, −1, ,
-
-
,
-
-
,
-
-
-
-
-
-
-
-
-
-
Answer may vary
-
6.4 Quadratic Functions and Their Graphs
Learning Objectives
- Graph a parabola.
- Find the intercepts and vertex of a parabola.
- Find the maximum and minimum y-value.
- Find the vertex of a parabola by completing the square.
The Graph of a Quadratic Function
A quadratic function is a polynomial function of degree 2 which can be written in the general form,
Here a, b and c represent real numbers where The squaring function is a quadratic function whose graph follows.
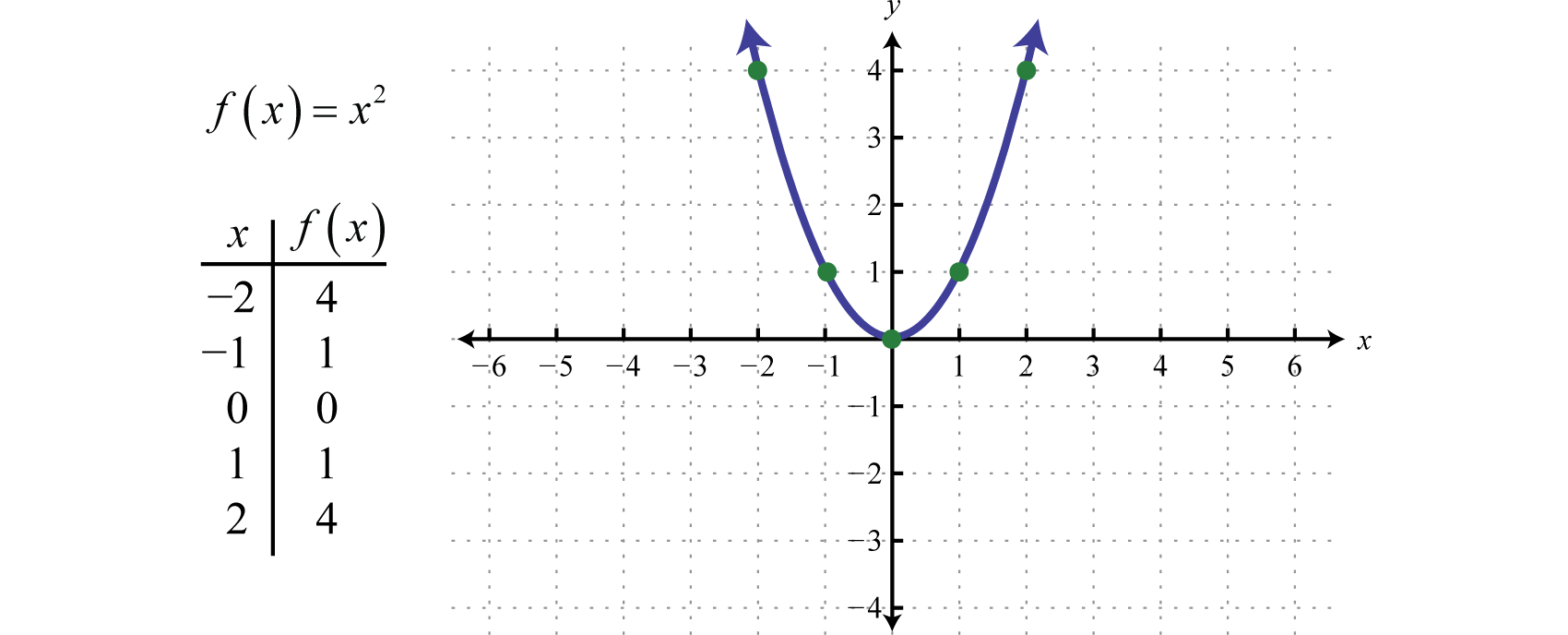
This general curved shape is called a parabolaThe U-shaped graph of any quadratic function defined by , where a, b, and c are real numbers and and is shared by the graphs of all quadratic functions. Note that the graph is indeed a function as it passes the vertical line test. Furthermore, the domain of this function consists of the set of all real numbers and the range consists of the set of nonnegative numbers
When graphing parabolas, we want to include certain special points in the graph. The y-intercept is the point where the graph intersects the y-axis. The x-intercepts are the points where the graph intersects the x-axis. The vertexThe point that defines the minimum or maximum of a parabola. is the point that defines the minimum or maximum of the graph. Lastly, the line of symmetryThe vertical line through the vertex, , about which the parabola is symmetric. (also called the axis of symmetryA term used when referencing the line of symmetry.) is the vertical line through the vertex, about which the parabola is symmetric.
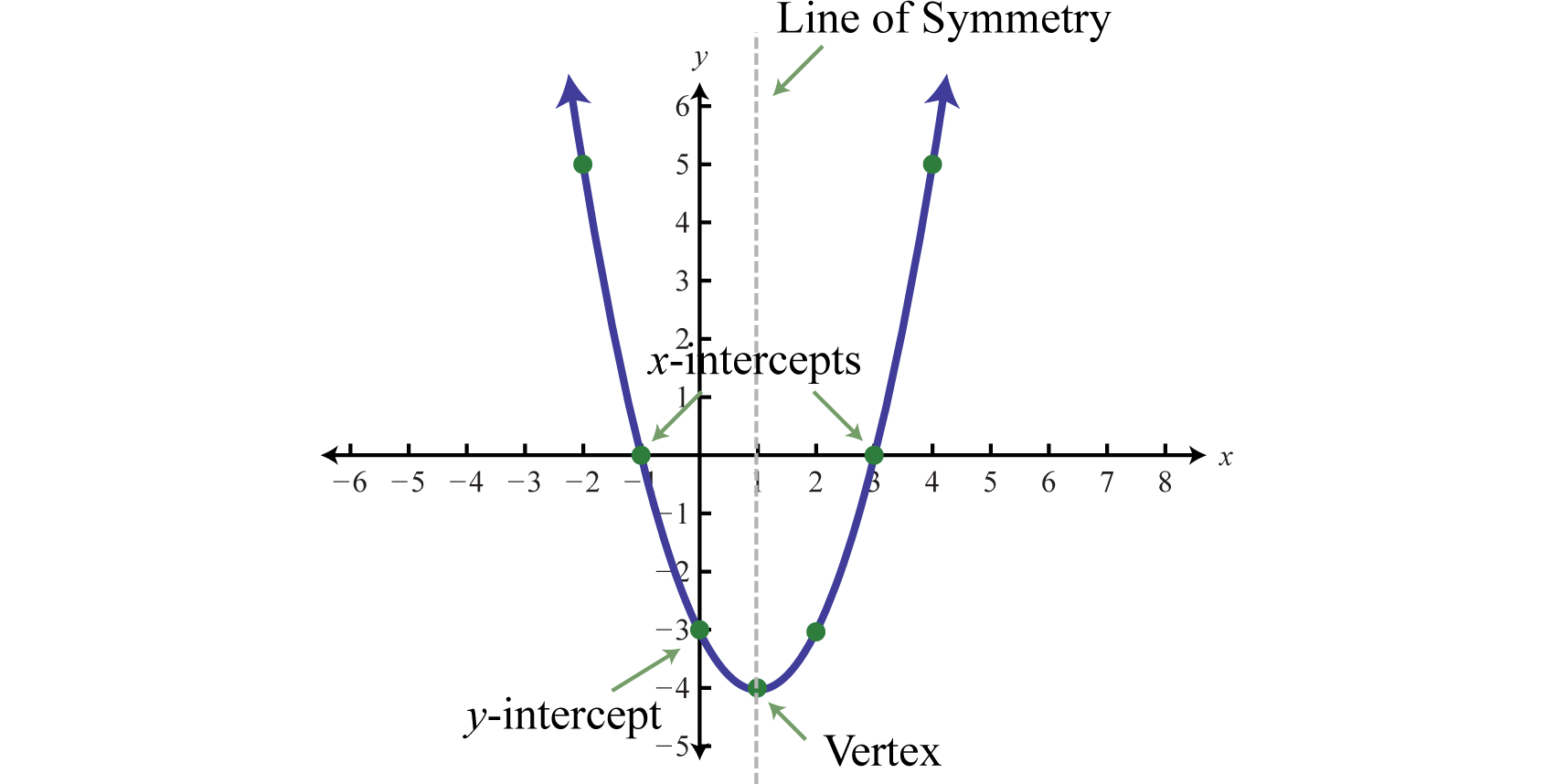
For any parabola, we will find the vertex and y-intercept. In addition, if the x-intercepts exist, then we will want to determine those as well. Guessing at the x-values of these special points is not practical; therefore, we will develop techniques that will facilitate finding them. Many of these techniques will be used extensively as we progress in our study of algebra.
Given a quadratic function , find the y-intercept by evaluating the function where In general, , and we have
Next, recall that the x-intercepts, if they exist, can be found by setting Doing this, we have , which has general solutions given by the quadratic formula, Therefore, the x-intercepts have this general form:
Using the fact that a parabola is symmetric, we can determine the vertical line of symmetry using the x-intercepts. To do this, we find the x-value midway between the x-intercepts by taking an average as follows:
Therefore, the line of symmetry is the vertical line We can use the line of symmetry to find the the vertex.
Generally three points determine a parabola. However, in this section we will find five points so that we can get a better approximation of the general shape. The steps for graphing a parabola are outlined in the following example.
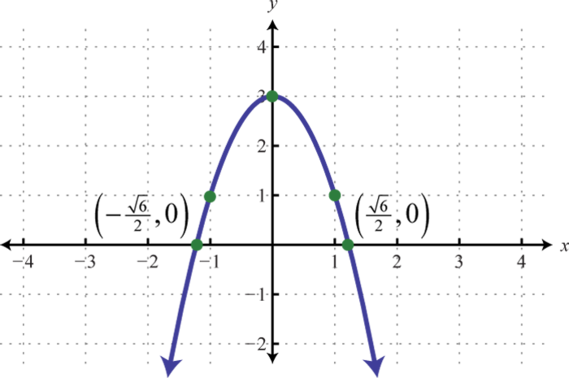
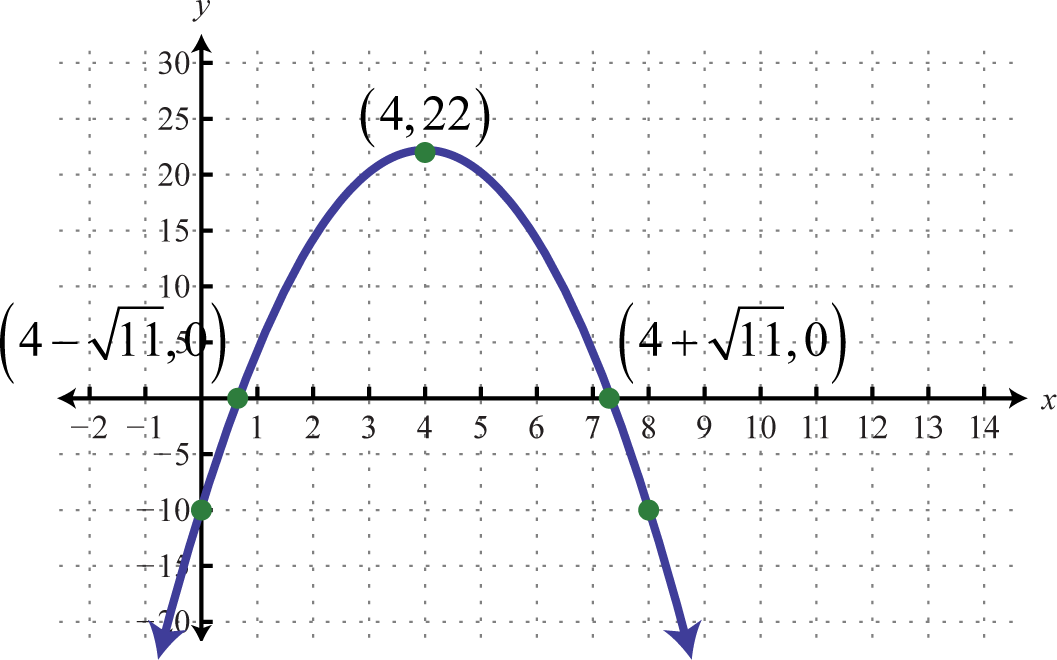
Example 1
Graph:
Solution:
Step 1: Determine the y-intercept. To do this, set and find
The y-intercept is
Step 2: Determine the x-intercepts if any. To do this, set and solve for x.
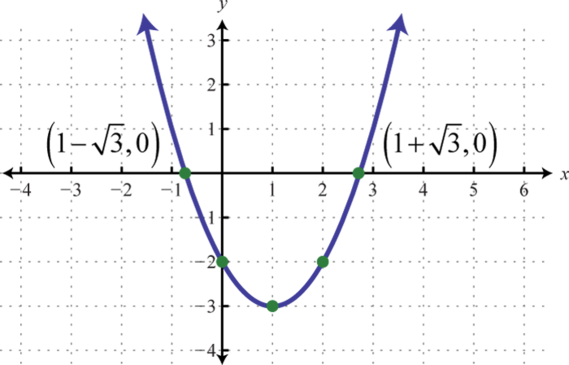
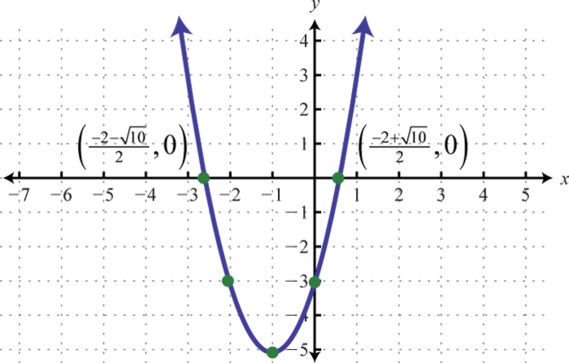
Here where , we obtain two solutions. Hence, there are two x-intercepts, and
Step 3: Determine the vertex. One way to do this is to first use to find the x-value of the vertex and then substitute this value in the function to find the corresponding y-value. In this example, and
Substitute −1 into the original function to find the corresponding y-value.
The vertex is
Step 4: Determine extra points so that we have at least five points to plot. Ensure a good sampling on either side of the line of symmetry. In this example, one other point will suffice. Choose and find the corresponding y-value.
Our fifth point is
Step 5: Plot the points and sketch the graph. To recap, the points that we have found are
Answer:
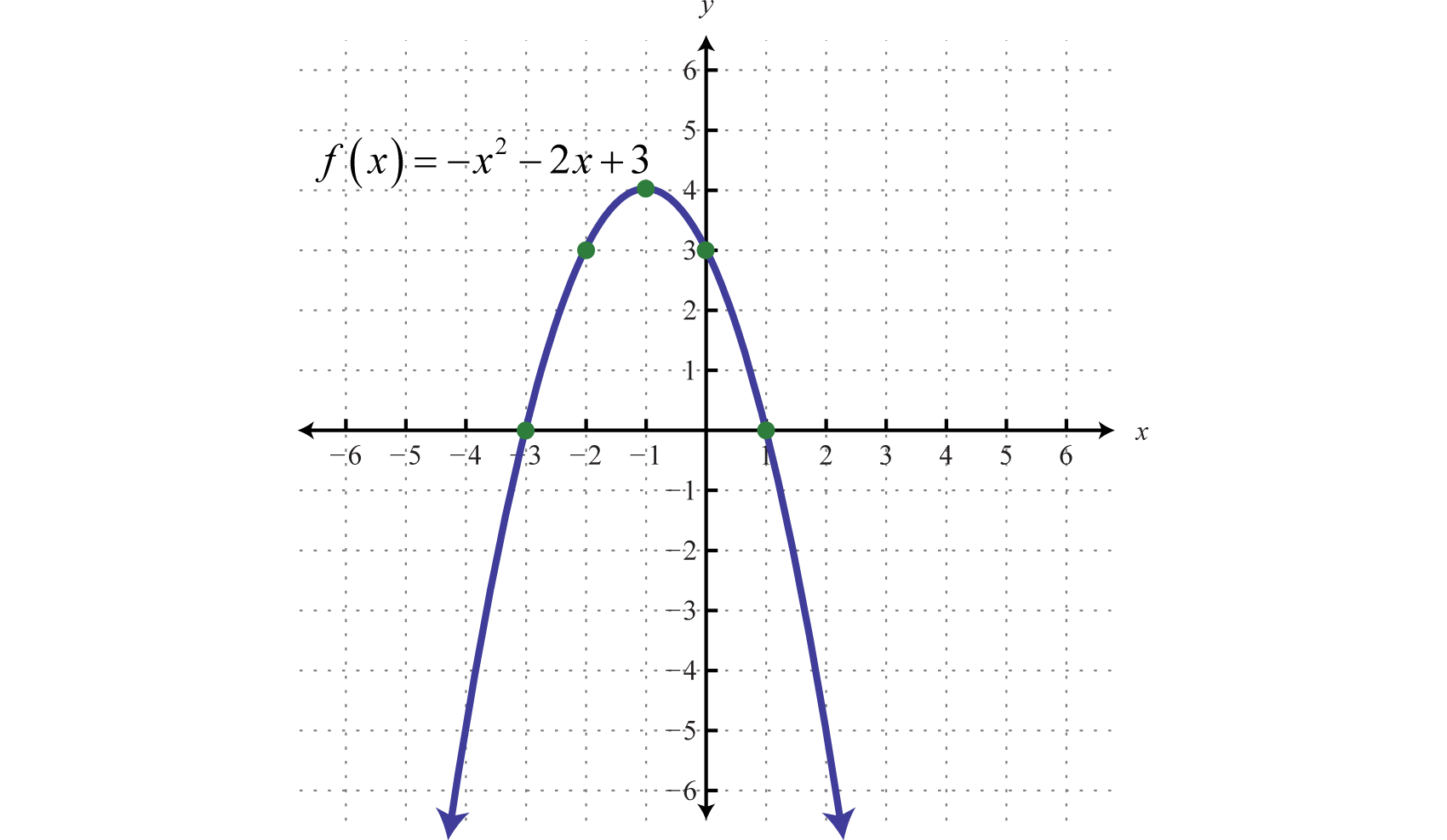
The parabola opens downward. In general, use the leading coefficient to determine if the parabola opens upward or downward. If the leading coefficient is negative, as in the previous example, then the parabola opens downward. If the leading coefficient is positive, then the parabola opens upward.
All quadratic functions of the form have parabolic graphs with y-intercept However, not all parabolas have x-intercepts.
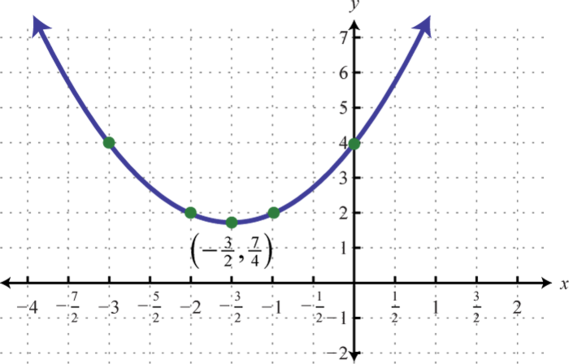
Example 2
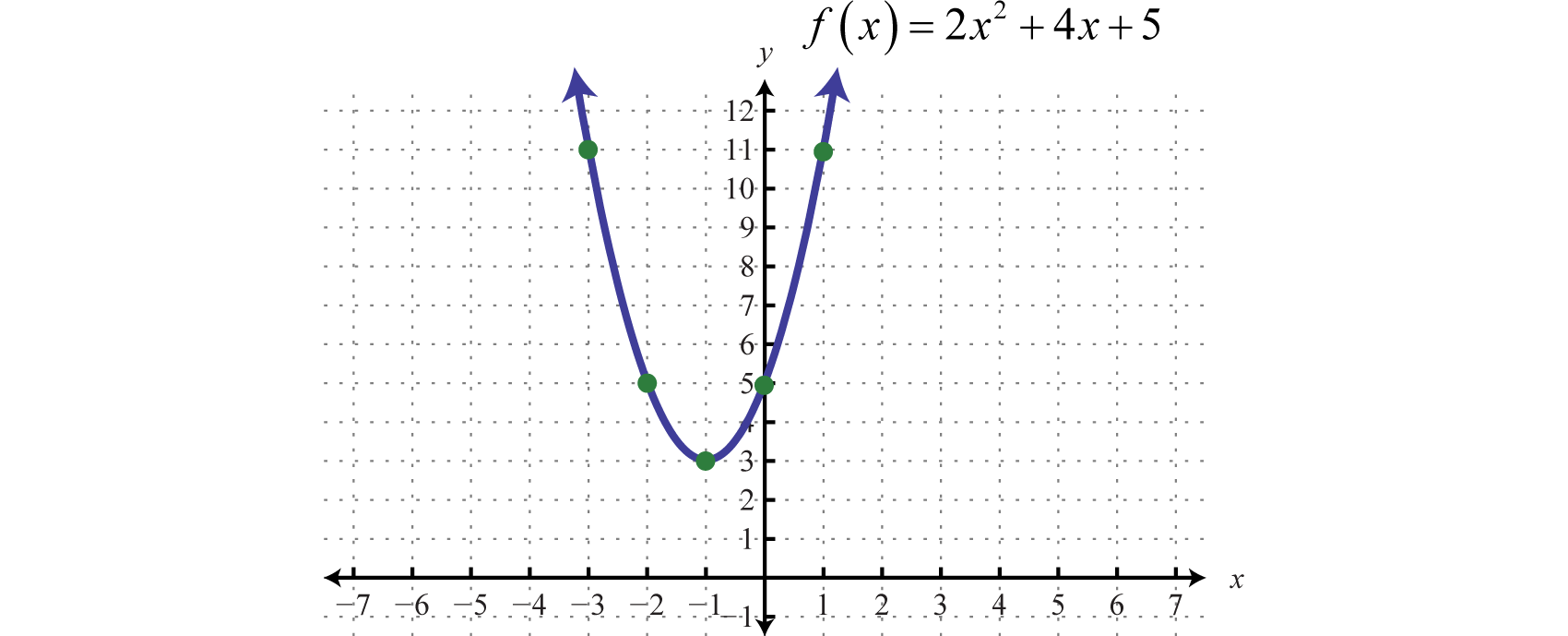
Graph:
Solution:
Because the leading coefficient 2 is positive, we note that the parabola opens upward. Here c = 5 and the y-intercept is (0, 5). To find the x-intercepts, set
In this case, a = 2, b = 4, and c = 5. Use the discriminant to determine the number and type of solutions.
Since the discriminant is negative, we conclude that there are no real solutions. Because there are no real solutions, there are no x-intercepts. Next, we determine the x-value of the vertex.
Given that the x-value of the vertex is −1, substitute −1 into the original equation to find the corresponding y-value.
The vertex is (−1, 3). So far, we have only two points. To determine three more, choose some x-values on either side of the line of symmetry, x = −1. Here we choose x-values −3, −2, and 1.
To summarize, we have
Plot the points and sketch the graph.
Answer:
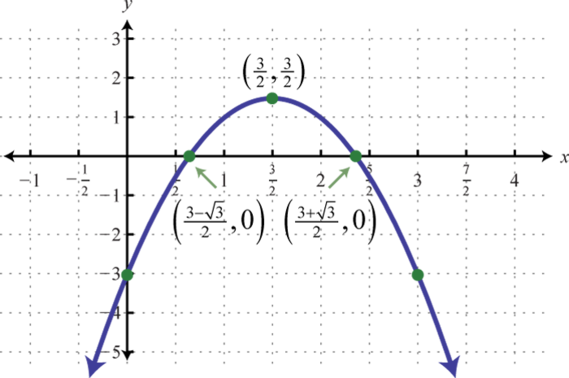
Example 3
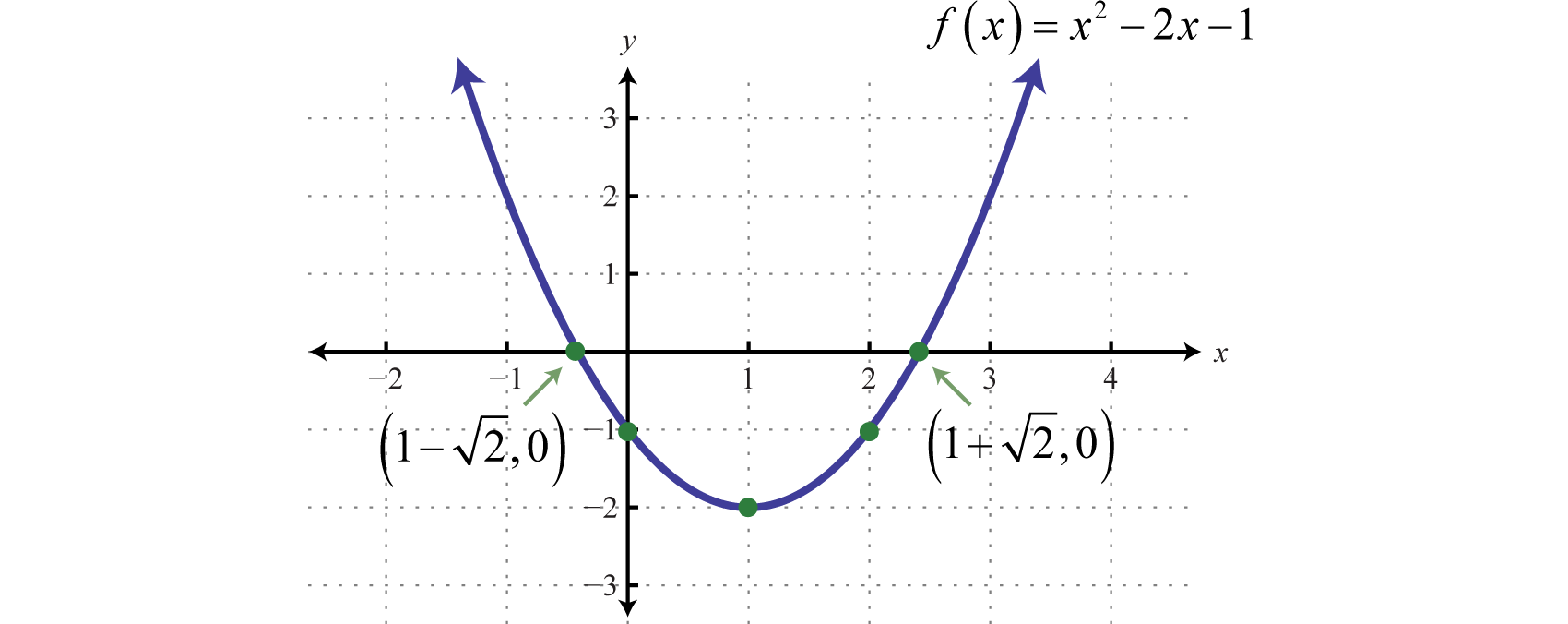
Graph:
Solution:
Since a = 1, the parabola opens upward. Furthermore, c = −1, so the y-intercept is To find the x-intercepts, set
In this case, solve using the quadratic formula with a = 1, b = −2, and c = −1.
Here we obtain two real solutions for x, and thus there are two x-intercepts:
Approximating the x-intercepts using a calculator will help us plot the points. However, we will present the exact x-intercepts on the graph. Next, find the vertex.
Given that the x-value of the vertex is 1, substitute into the original equation to find the corresponding y-value.
The vertex is (1, −2). We need one more point.
To summarize, we have
Plot the points and sketch the graph.
Answer:
Finding the Maximum or Minimum
It is often useful to find the maximum and/or minimum values of functions that model real-life applications. To find these important values given a quadratic function, we use the vertex. If the leading coefficient a is positive, then the parabola opens upward and there will be a minimum y-value. If the leading coefficient a is negative, then the parabola opens downward and there will be a maximum y-value.
Example 4
Determine the maximum or minimum:
Solution:
Since a = −4, we know that the parabola opens downward and there will be a maximum y-value. To find it, first find the x-value of the vertex.
The x-value of the vertex is 3. Substitute this value into the original equation to find the corresponding y-value.
The vertex is (3, 1). Therefore, the maximum y-value is 1, which occurs where x = 3, as illustrated below:
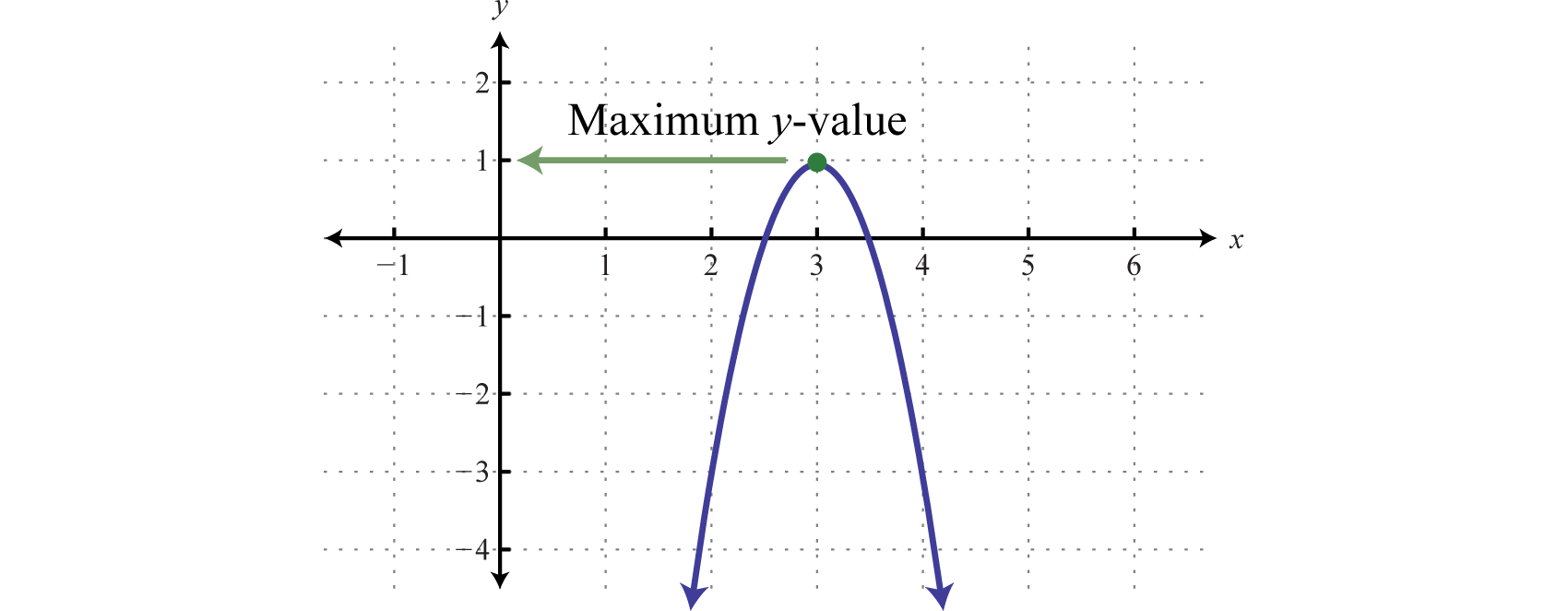
Note: The graph is not required to answer this question.
Answer: The maximum is 1.
Example 5
Determine the maximum or minimum:
Solution:
Since a = 4, the parabola opens upward and there is a minimum y-value. Begin by finding the x-value of the vertex.
Substitute x = 4 into the original equation to find the corresponding y-value.
The vertex is (4, −2). Therefore, the minimum y-value of −2 occurs where x = 4, as illustrated below:
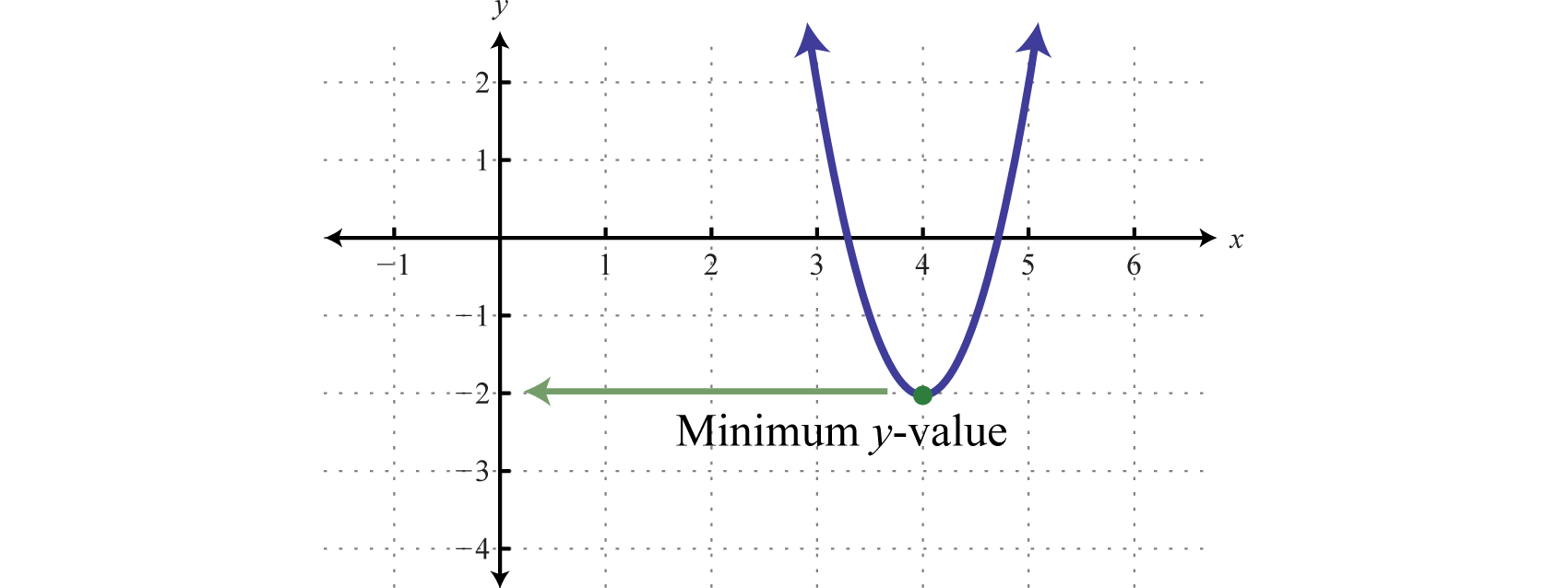
Answer: The minimum is −2.
Example 6
The height in feet of a projectile is given by the function , where t represents the time in seconds after launch. What is the maximum height reached by the projectile?
Solution:
Here , and the parabola opens downward. Therefore, the y-value of the vertex determines the maximum height. Begin by finding the time at which the vertex occurs.
The maximum height will occur in seconds (or seconds). Substitute this time into the function to determine the maximum height attained.
Answer: The maximum height of the projectile is 81 feet.
Finding the Vertex by Completing the Square
In this section, we demonstrate an alternate approach for finding the vertex. Any quadratic function can be rewritten in vertex formA quadratic function written in the form ,
In this form, the vertex is To see that this is the case, consider graphing using the transformations.
Use these translations to sketch the graph,
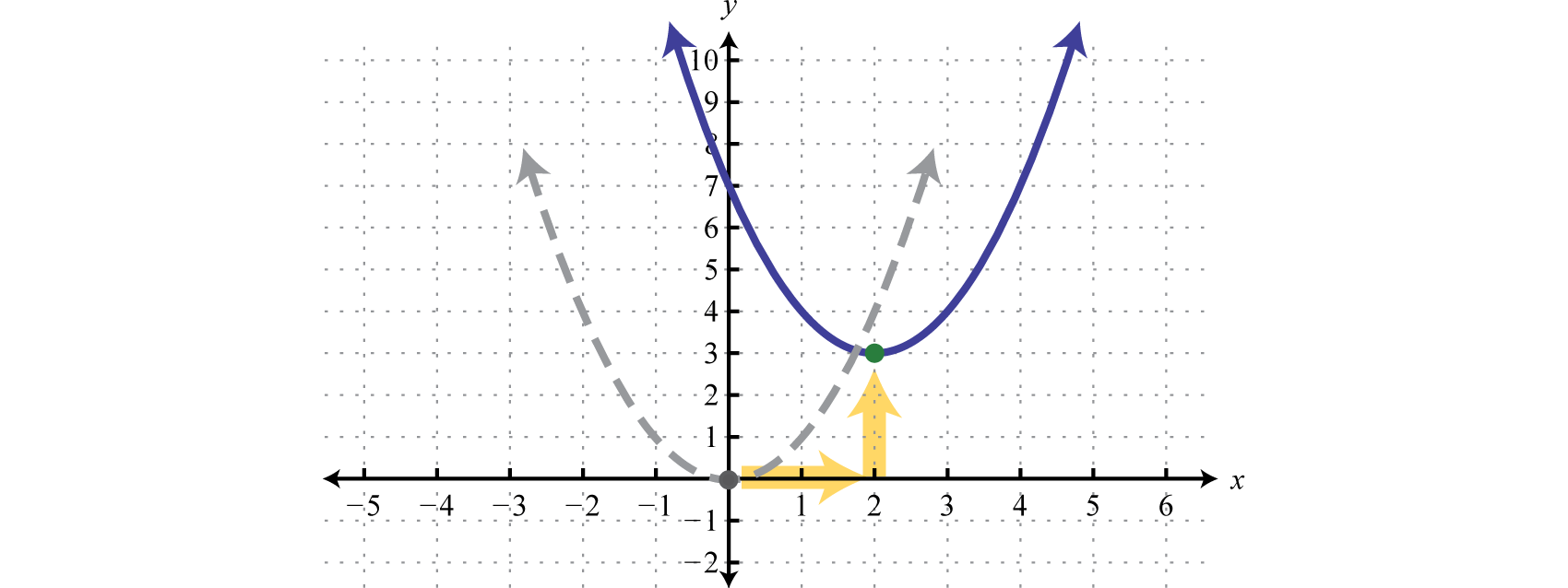
Here we can see that the vertex is (2, 3).
When the equation is in this form, we can read the vertex directly from it.
Example 7
Determine the vertex:
Solution:
Rewrite the equation as follows before determining h and k.
Here h = −3 and k = −2.
Answer: The vertex is (−3, −2).
Often the equation is not given in vertex form. To obtain this form, complete the square.
Example 8
Rewrite in vertex form and determine the vertex:
Solution:
Begin by making room for the constant term that completes the square.
The idea is to add and subtract the value that completes the square, , and then factor. In this case, add and subtract
Adding and subtracting the same value within an expression does not change it. Doing so is equivalent to adding 0. Once the equation is in this form, we can easily determine the vertex.
Here h = −2 and k = 5.
Answer: The vertex is (−2, 5).
If there is a leading coefficient other than 1, then we must first factor out the leading coefficient from the first two terms of the trinomial.
Example 9
Rewrite in vertex form and determine the vertex:
Solution:
Since a = 2, factor this out of the first two terms in order to complete the square. Leave room inside the parentheses to add and subtract the value that completes the square.
Now use −2 to determine the value that completes the square. In this case, Add and subtract 1 and factor as follows:
In this form, we can easily determine the vertex.
Here h = 1 and k = 6.
Answer: The vertex is (1, 6).
Key Takeaways
- The graph of any quadratic function , where a, b, and c are real numbers and , is called a parabola.
- When graphing a parabola always find the vertex and the y-intercept. If the x-intercepts exist, find those as well. Also, be sure to find ordered pair solutions on either side of the line of symmetry,
- Use the leading coefficient, a, to determine if a parabola opens upward or downward. If a is positive, then it opens upward. If a is negative, then it opens downward.
- The vertex of any parabola has an x-value equal to After finding the x-value of the vertex, substitute it into the original equation to find the corresponding y-value. This y-value is a maximum if the parabola opens downward, and it is a minimum if the parabola opens upward.
- The domain of a parabola opening upward or downward consists of all real numbers. The range is bounded by the y-value of the vertex.
- An alternate approach to finding the vertex is to rewrite the quadratic function in the form When in this form, the vertex is and can be read directly from the equation. To obtain this form, take and complete the square.
Topic Exercises
Part A: The Graph of Quadratic Functions
Does the parabola open upward or downward? Explain.
Determine the x- and y-intercepts.
Find the vertex and the line of symmetry.
Graph. Find the vertex and the y-intercept. In addition, find the x-intercepts if they exist.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
The height in feet reached by a baseball tossed upward at a speed of 48 feet per second from the ground is given by the function , where t represents the time in seconds after the ball is thrown. What is the baseball’s maximum height and how long does it take to attain that height?
-
The height in feet of a projectile launched straight up from a mound is given by the function , where t represents seconds after launch. What is the maximum height?
-
The profit in dollars generated by producing and selling x custom lamps is given by the function What is the maximum profit?
-
The profit in dollars generated from producing and selling a particular item is modeled by the formula , where x represents the number of units produced and sold. What number of units must be produced and sold to maximize revenue?
-
The average number of hits to a radio station Web site is modeled by the formula , where t represents the number of hours since 8:00 a.m. At what hour of the day is the number of hits to the Web site at a minimum?
-
The value in dollars of a new car is modeled by the formula , where t represents the number of years since it was purchased. Determine the minimum value of the car.
-
The daily production cost in dollars of a textile manufacturing company producing custom uniforms is modeled by the formula , where x represents the number of uniforms produced.
- How many uniforms should be produced to minimize the daily production costs?
- What is the minimum daily production cost?
-
The area in square feet of a certain rectangular pen is given by the formula , where w represents the width in feet. Determine the width that produces the maximum area.
Part B: Finding the Maximum or Minimum
Determine the maximum or minimum y-value.
Given the following quadratic functions, determine the domain and range.
Part C: Finding the Vertex by Completing the Square
Determine the vertex.
Rewrite in vertex form and determine the vertex.
Graph. Find the vertex and the y-intercept. In addition, find the x-intercepts if they exist.
-
Write down your plan for graphing a parabola on an exam. What will you be looking for and how will you present your answer? Share your plan on the discussion board.
-
Why is any parabola that opens upward or downward a function? Explain to a classmate how to determine the domain and range.
-
Research and discuss ways of finding a quadratic function that has a graph passing through any three given points. Share a list of steps as well as an example of how to do this.
Part D: Discussion Board
Answers
-
Upward
-
-
Downward
-
-
Downward
-
-
x-intercepts: (−6, 0), (2, 0);y-intercept: (0, −12)
-
-
x-intercepts: (−3, 0), ; y-intercept: (0, −3)
-
-
x-intercepts: (−1, 0), ; y-intercept: (0, 2)
-
-
x-intercepts: , ; y-intercept: (0, −27)
-
-
x-intercepts: none; y-intercept: (0, 1)
-
-
Vertex: (5, −9); line of symmetry:
-
-
Vertex: ; line of symmetry:
-
-
Vertex: (0, −1); line of symmetry:
-
-
-
-
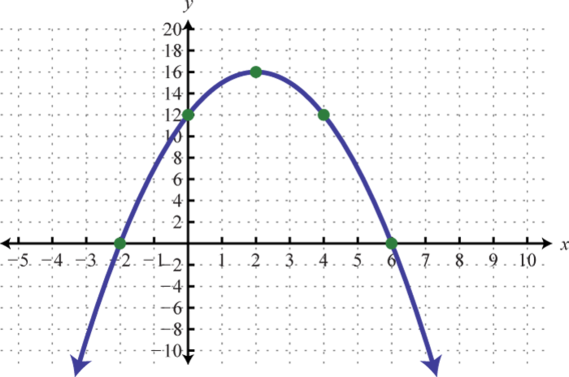
-
-
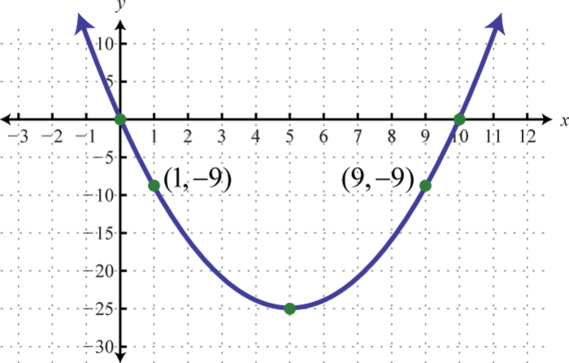
-
-
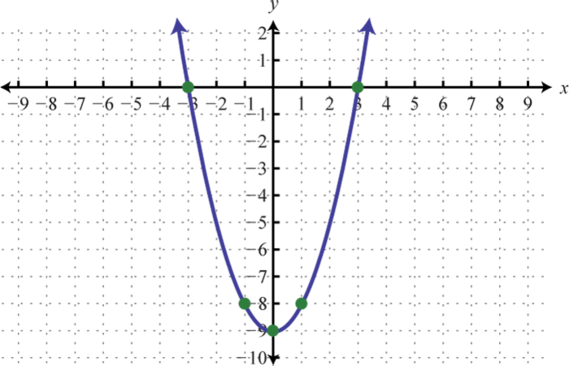
-
-
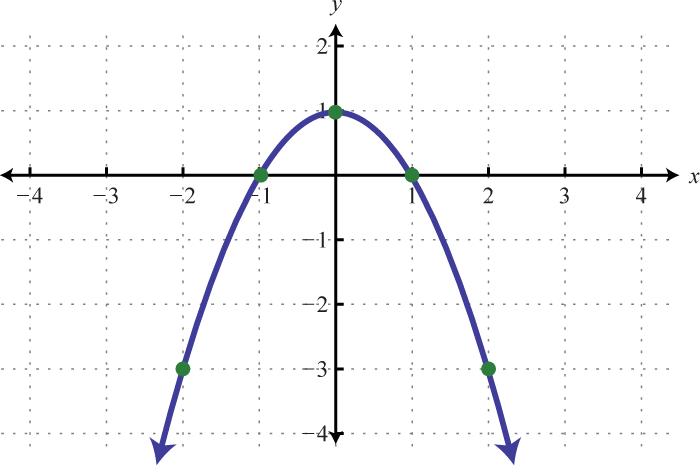
-
-
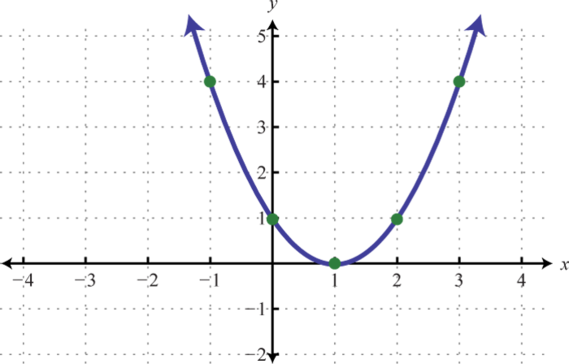
-
-
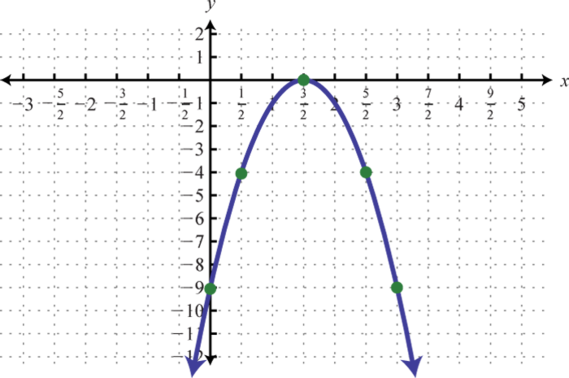
-
-
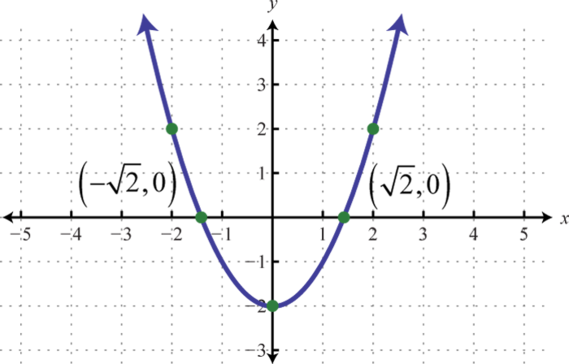
-
-
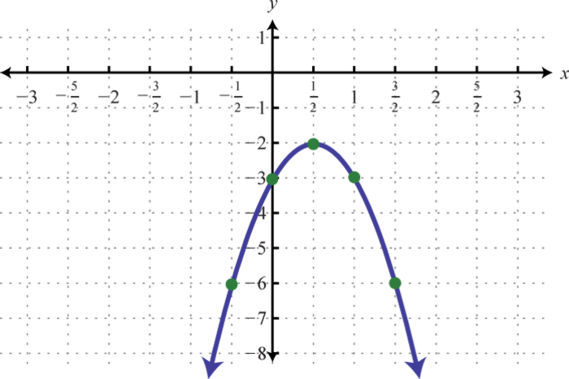
-
-
-
-
-
-
-
-
-
-
-
-
Maximum: y = 10
-
-
Minimum: y = 4
-
-
Maximum: y = 0
-
-
Maximum: y = 10
-
-
Minimum:
-
-
Minimum:
-
-
Domain: ; range:
-
-
Domain: ; range:
-
-
Domain: ; range:
-
-
The maximum height of 36 feet occurs after 1.5 seconds.
-
-
$4,000
-
-
12:00 p.m.
-
-
- 500 uniforms
- $5,000
-
-
(5, 3)
-
-
(−1, 6)
-
-
(−8, −1)
-
-
; vertex: (7, −25)
-
-
; vertex: (−2, −16)
-
-
; vertex: (3, −21)
-
-
; vertex: (8, 81)
-
-
-
-
-
-
-
-
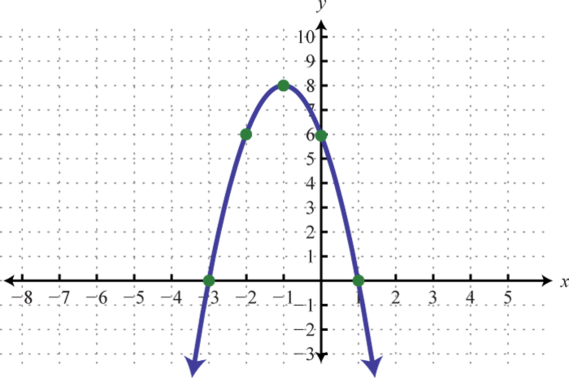
-
-
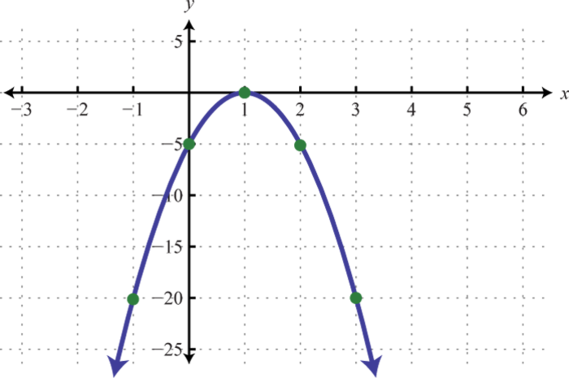
-
-
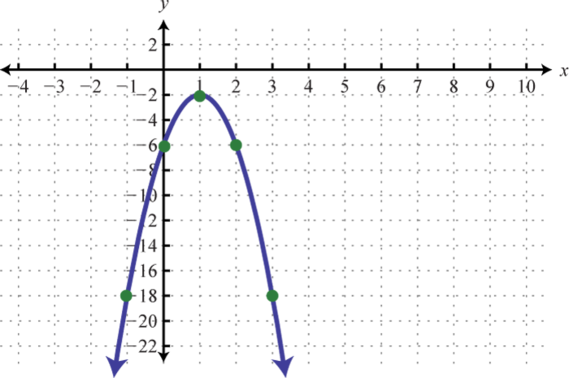
-
-
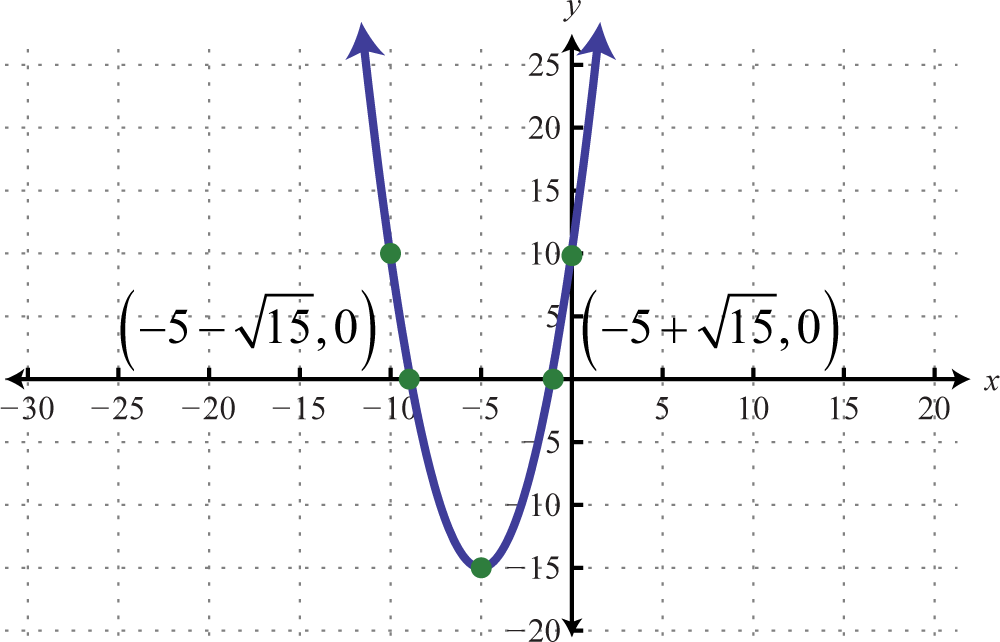
-
-
-
-
Answer may vary
-
-
Answer may vary
6.5 Solving Quadratic Inequalities
Learning Objectives
- Check solutions to quadratic inequalities with one variable.
- Understand the geometric relationship between solutions to quadratic inequalities and their graphs.
- Solve quadratic inequalities.
Solutions to Quadratic Inequalities
A quadratic inequalityA mathematical statement that relates a quadratic expression as either less than or greater than another. is a mathematical statement that relates a quadratic expression as either less than or greater than another. Some examples of quadratic inequalities solved in this section follow.
A solution to a quadratic inequality is a real number that will produce a true statement when substituted for the variable.
Example 1
Are −3, −2, and −1 solutions to ?
Solution:
Substitute the given value in for x and simplify.
Answer: −2 and −1 are solutions and −3 is not.
Quadratic inequalities can have infinitely many solutions, one solution, or no solution. If there are infinitely many solutions, graph the solution set on a number line and/or express the solution using interval notation. Graphing the function defined by found in the previous example we have
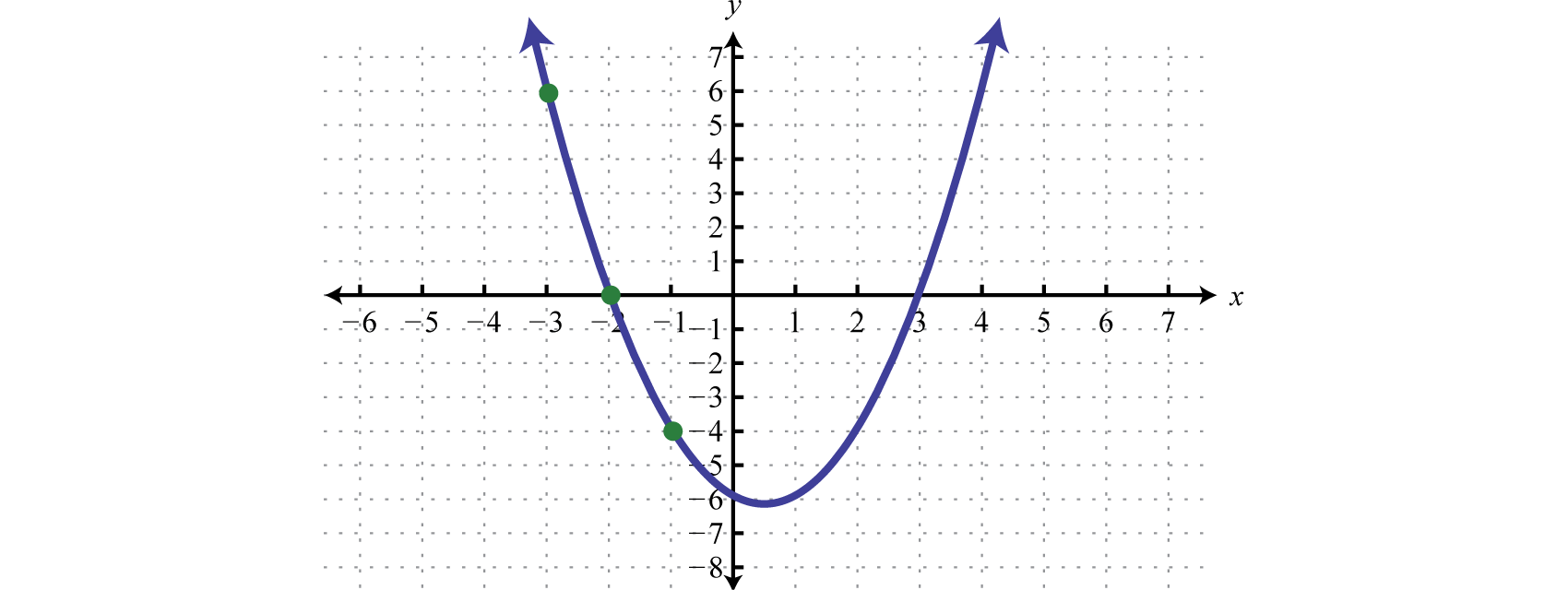
The result of evaluating for any x-value will be negative, zero, or positive.
The values in the domain of a function that separate regions that produce positive or negative results are called critical numbersThe values in the domain of a function that separate regions that produce positive or negative results.. In the case of a quadratic function, the critical numbers are the roots, sometimes called the zeros. For example, has roots −2 and 3. These values bound the regions where the function is positive (above the x-axis) or negative (below the x-axis).
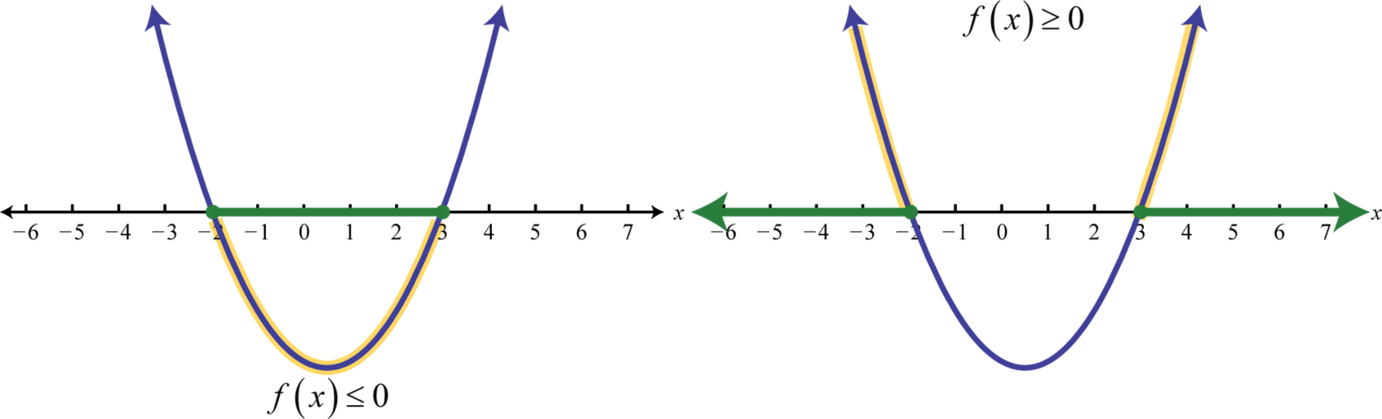
Therefore has solutions where , using interval notation Furthermore, has solutions where or , using interval notation
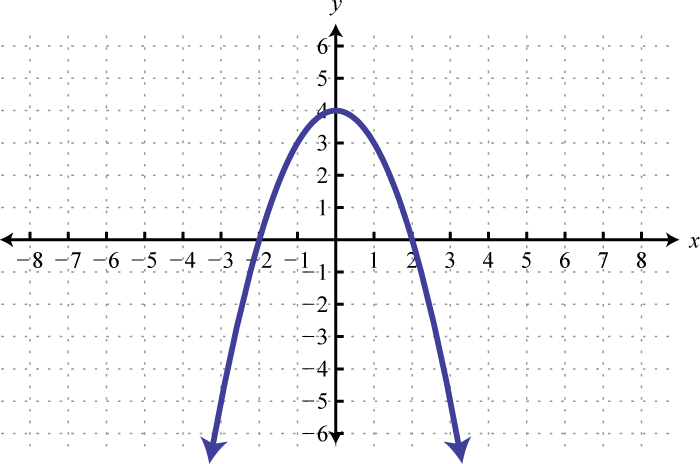
Example 2
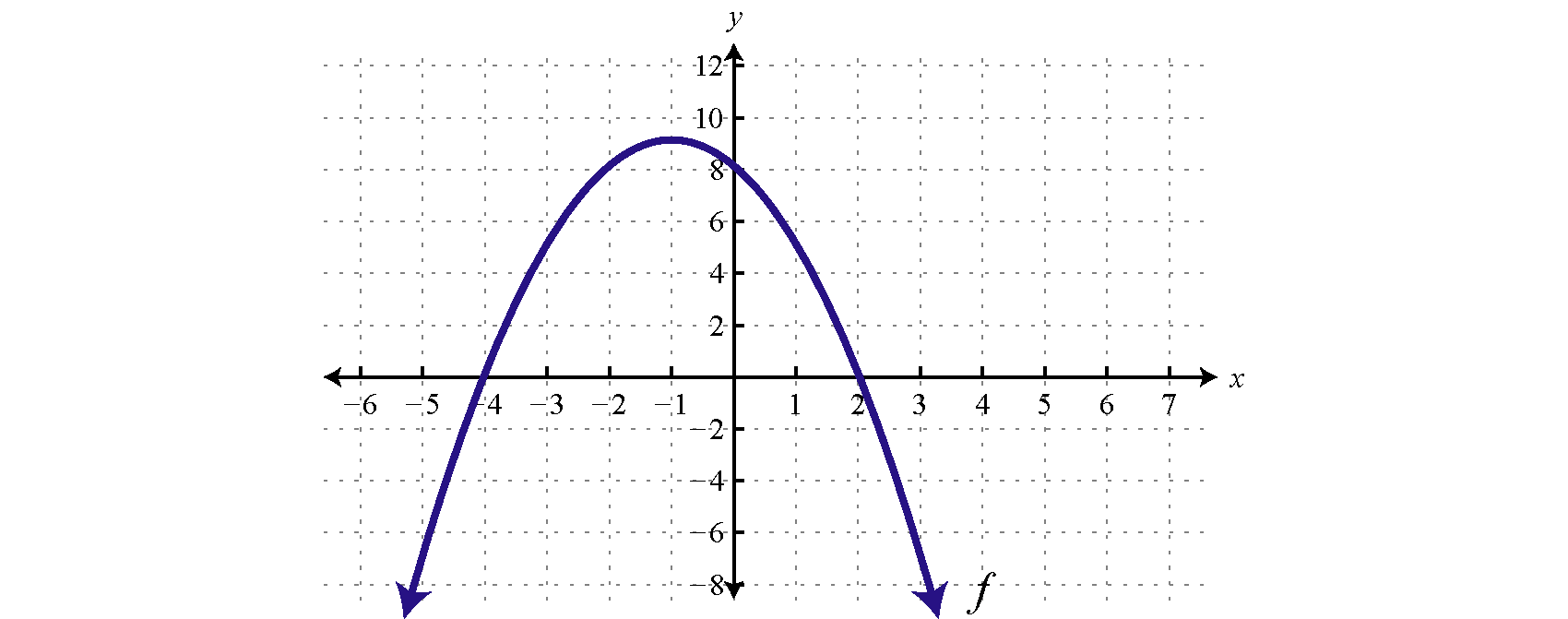
Given the graph of determine the solutions to :
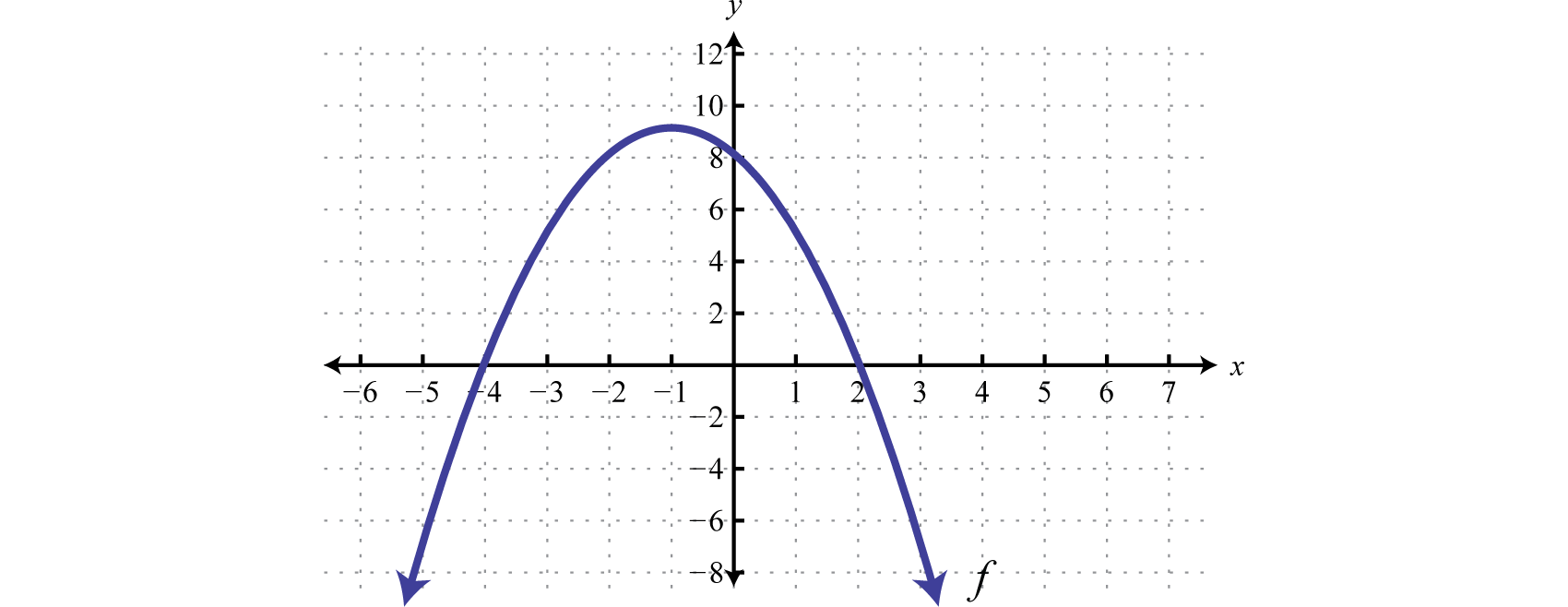
Solution:
From the graph we can see that the roots are −4 and 2. The graph of the function lies above the x-axis () in between these roots.
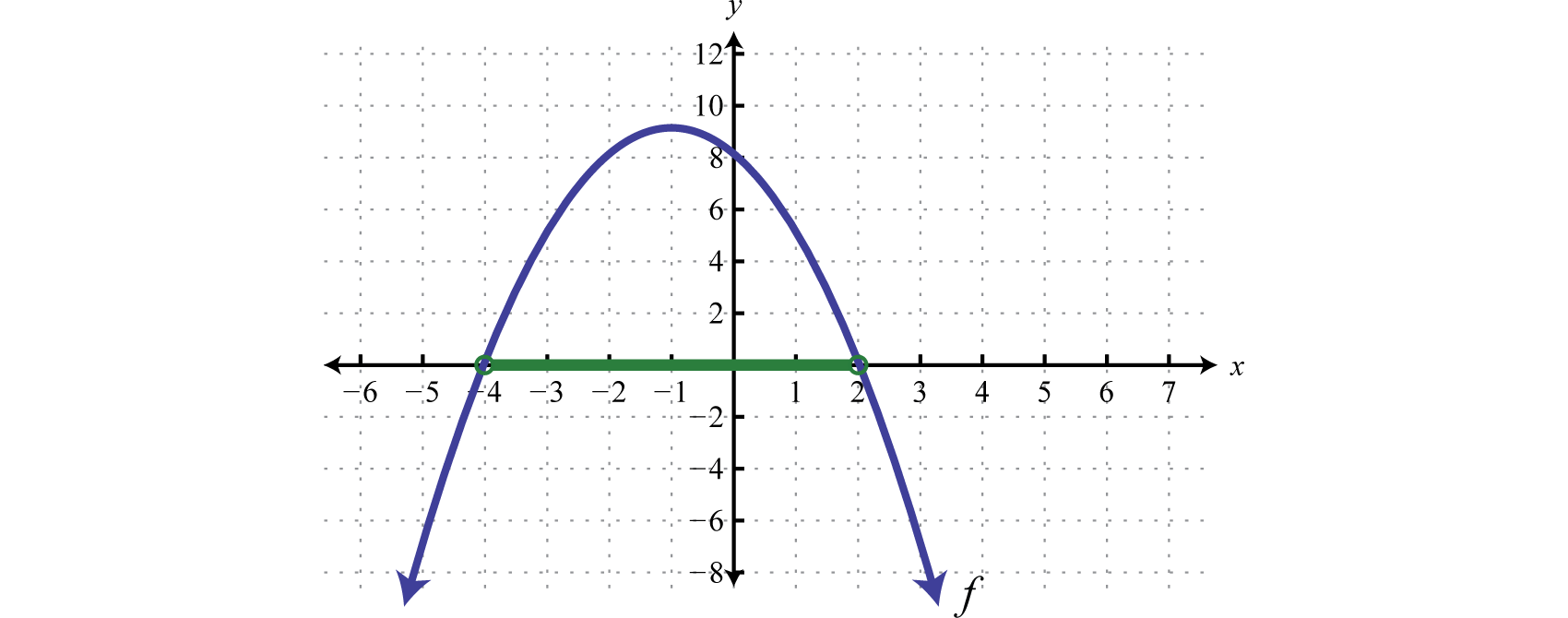
Because of the strict inequality, the solution set is shaded with an open dot on each of the boundaries. This indicates that these critical numbers are not actually included in the solution set. This solution set can be expressed two ways,
In this textbook, we will continue to present answers in interval notation.
Answer:
Solving Quadratic Inequalities
Next we outline a technique used to solve quadratic inequalities without graphing the parabola. To do this we make use of a sign chartA model of a function using a number line and signs (+ or −) to indicate regions in the domain where the function is positive or negative. which models a function using a number line that represents the x-axis and signs (+ or −) to indicate where the function is positive or negative. For example,
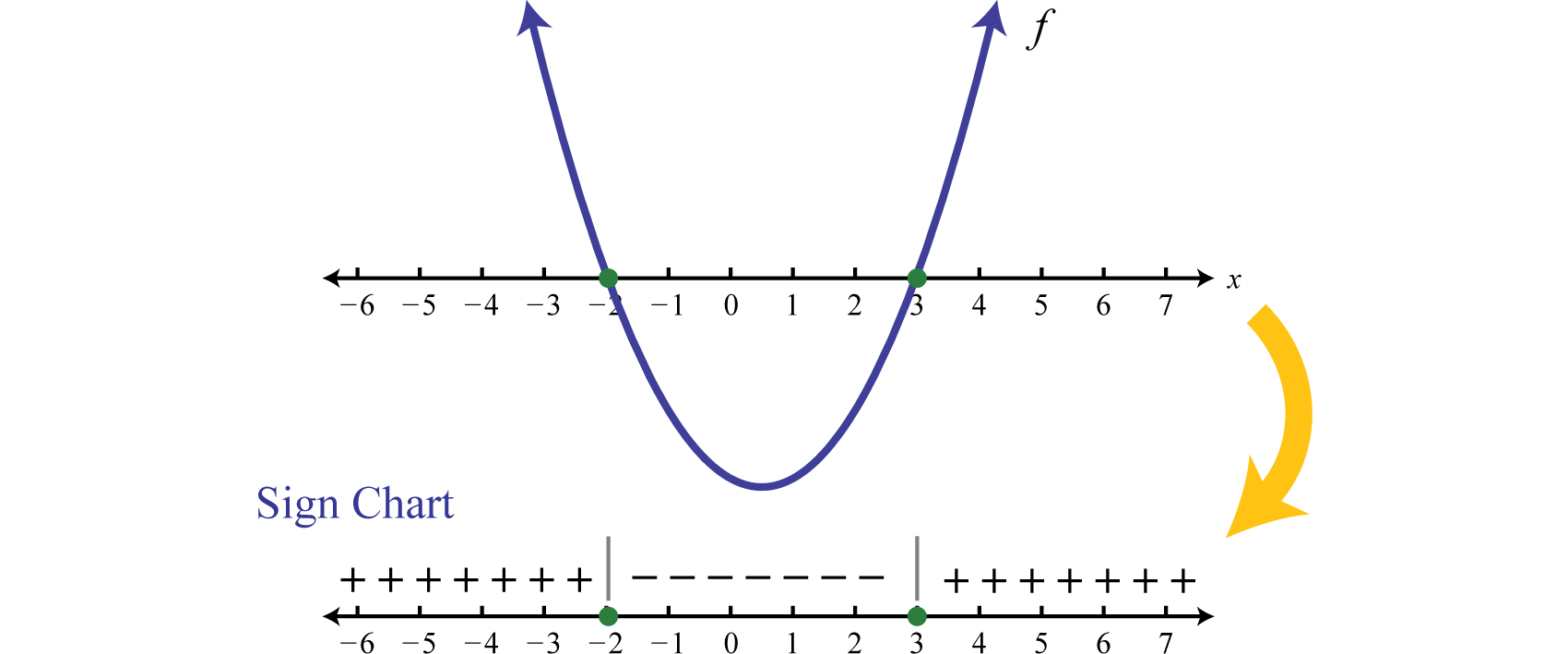
The plus signs indicate that the function is positive on the region. The negative signs indicate that the function is negative on the region. The boundaries are the critical numbers, −2 and 3 in this case. Sign charts are useful when a detailed picture of the graph is not needed and are used extensively in higher level mathematics. The steps for solving a quadratic inequality with one variable are outlined in the following example.
Example 3
Solve:
Solution:
It is important to note that this quadratic inequality is in standard form, with zero on one side of the inequality.
Step 1: Determine the critical numbers. For a quadratic inequality in standard form, the critical numbers are the roots. Therefore, set the function equal to zero and solve.
The critical numbers are −1 and 7.
Step 2: Create a sign chart. Since the critical numbers bound the regions where the function is positive or negative, we need only test a single value in each region. In this case the critical numbers partition the number line into three regions and we choose test values , , and
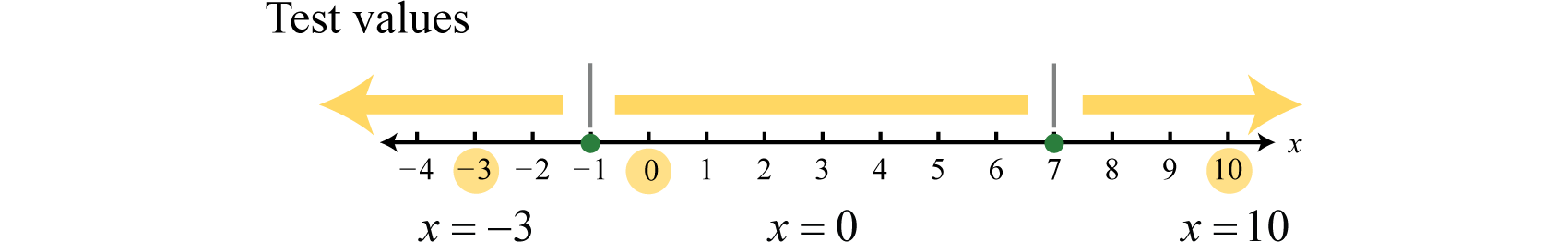
Test values may vary. In fact, we need only determine the sign (+ or −) of the result when evaluating Here we evaluate using the factored form.
Since the result of evaluating for −3 was negative, we place negative signs above the first region. The result of evaluating for 0 was positive, so we place positive signs above the middle region. Finally, the result of evaluating for 10 was negative, so we place negative signs above the last region, and the sign chart is complete.
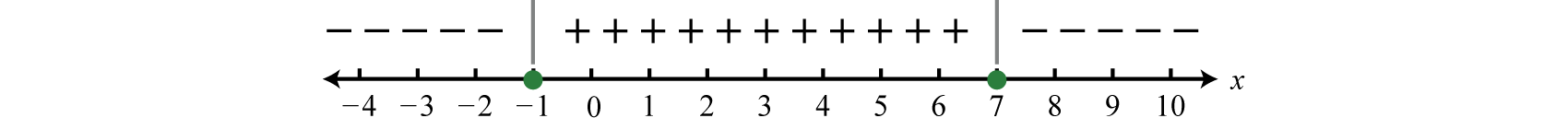
Step 3: Use the sign chart to answer the question. In this case, we are asked to determine where , or where the function is positive or zero. From the sign chart we see this occurs when x-values are inclusively between −1 and 7.

Using interval notation, the shaded region is expressed as The graph is not required; however, for the sake of completeness it is provided below.
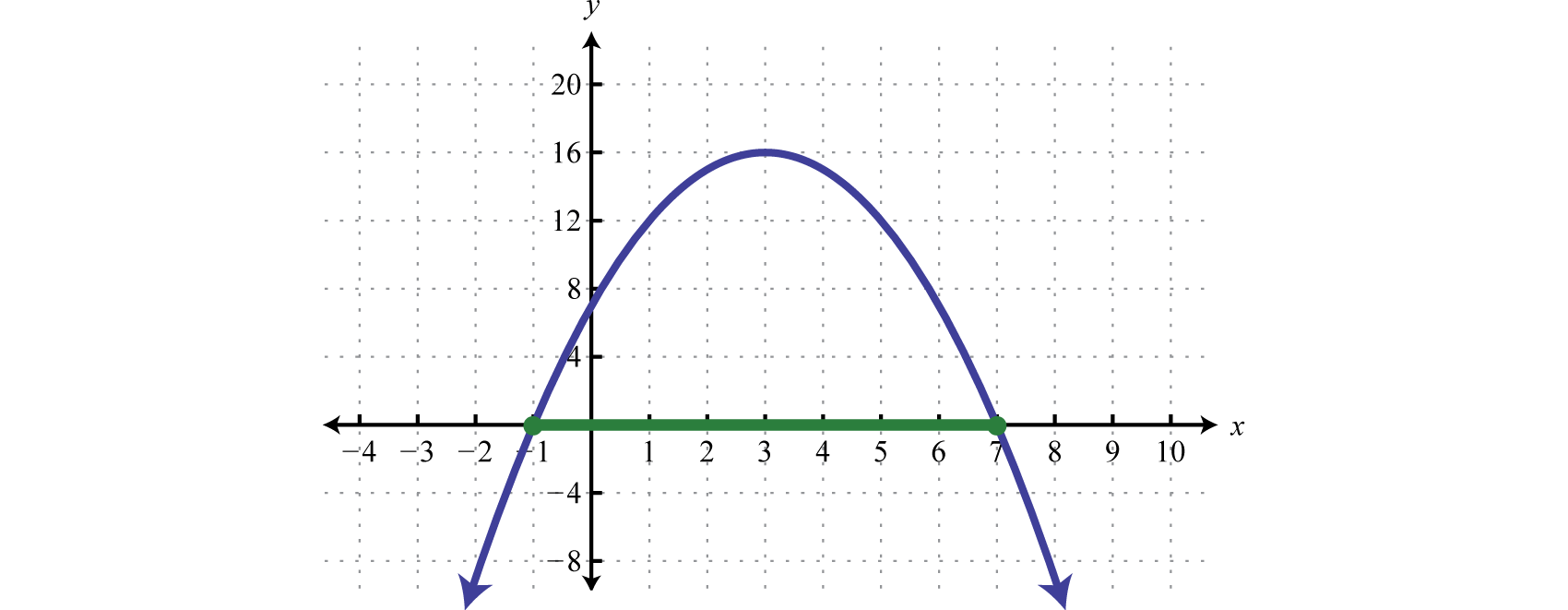
Indeed the function is greater than or equal to zero, above or on the x-axis, for x-values in the specified interval.
Answer:
Example 4
Solve:
Solution:
Begin by finding the critical numbers, in this case, the roots of
The critical numbers are and 3. Because of the strict inequality > we will use open dots.

Next choose a test value in each region and determine the sign after evaluating Here we choose test values −1, 2, and 5.
And we can complete the sign chart.

The question asks us to find the x-values that produce positive results (greater than zero). Therefore, shade in the regions with a + over them. This is the solution set.

Answer:
Sometimes the quadratic function does not factor. In this case we can make use of the quadratic formula.
Example 5
Solve:
Solution:
Find the critical numbers.
Identify a, b, and c for use in the quadratic formula. Here , , and Substitute the appropriate values into the quadratic formula and then simplify.
Therefore the critical numbers are and Use a closed dot on the number to indicate that these values will be included in the solution set.

Here we will use test values −5, 0, and 7.
After completing the sign chart shade in the values where the function is negative as indicated by the question ().

Answer:
It may be the case that there are no critical numbers.
Example 6
Solve:
Solution:
To find the critical numbers solve,
Substitute , , and into the quadratic formula and then simplify.
Because the solutions are not real, we conclude there are no real roots; hence there are no critical numbers. When this is the case, the graph has no x-intercepts and is completely above or below the x-axis. We can test any value to create a sign chart. Here we choose
Because the test value produced a positive result the sign chart looks as follows:
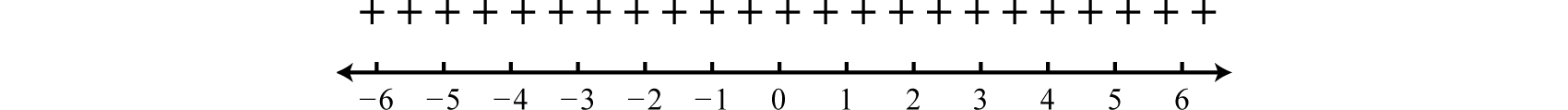
We are looking for the values where ; the sign chart implies that any real number for x will satisfy this condition.

Answer:
The function in the previous example is graphed below.
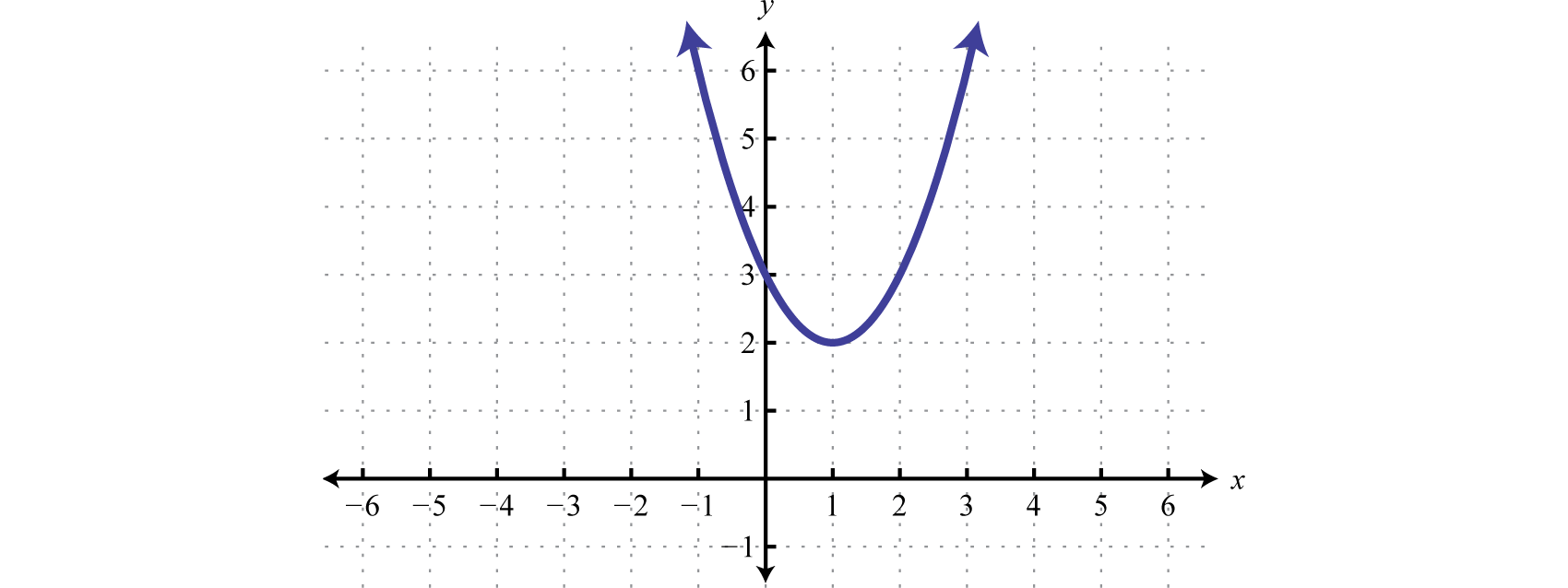
We can see that it has no x-intercepts and is always above the x-axis (positive). If the question was to solve , then the answer would have been no solution. The function is never negative.
Example 7
Find the domain:
Solution:
Recall that the argument of a square root function must be nonnegative. Therefore, the domain consists of all real numbers for x such that is greater than or equal to zero.
It should be clear that has two solutions ; these are the critical values. Choose test values in each interval and evaluate
Shade in the x-values that produce positive results.

Answer: Domain:
Key Takeaways
- Quadratic inequalities can have infinitely many solutions, one solution or no solution.
- We can solve quadratic inequalities graphically by first rewriting the inequality in standard form, with zero on one side. Graph the quadratic function and determine where it is above or below the x-axis. If the inequality involves “less than,” then determine the x-values where the function is below the x-axis. If the inequality involves “greater than,” then determine the x-values where the function is above the x-axis.
- We can streamline the process of solving quadratic inequalities by making use of a sign chart. A sign chart gives us a visual reference that indicates where the function is above the x-axis using positive signs or below the x-axis using negative signs. Shade in the appropriate x-values depending on the original inequality.
- To make a sign chart, use the function and test values in each region bounded by the roots. We are only concerned if the function is positive or negative and thus a complete calculation is not necessary.
Topic Exercises
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
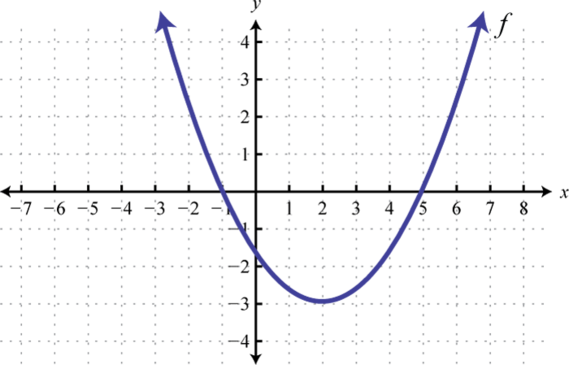
-
;
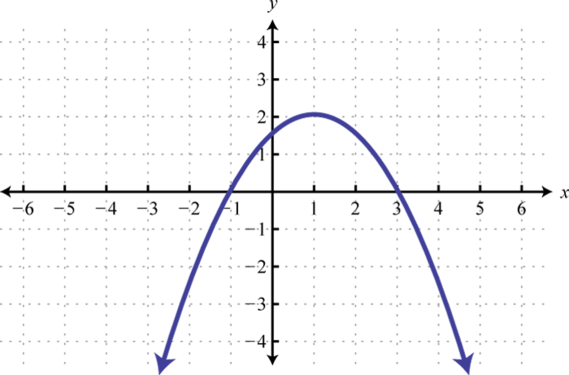
-
;
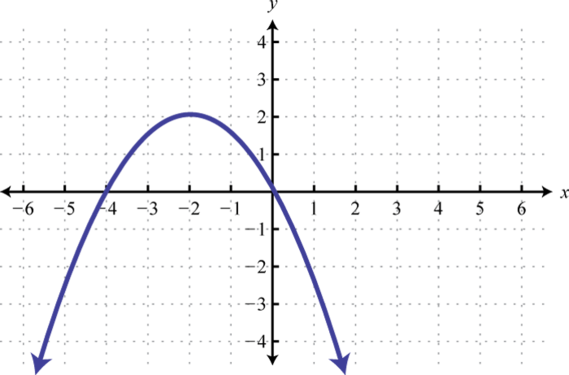
-
;
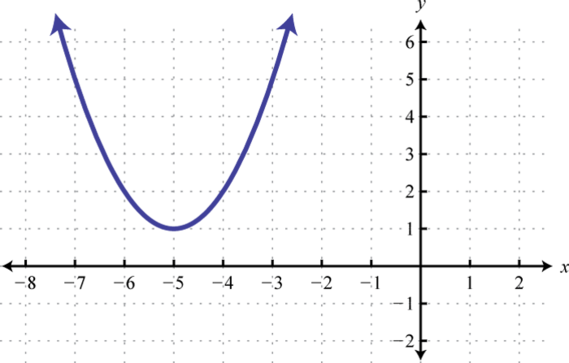
-
;
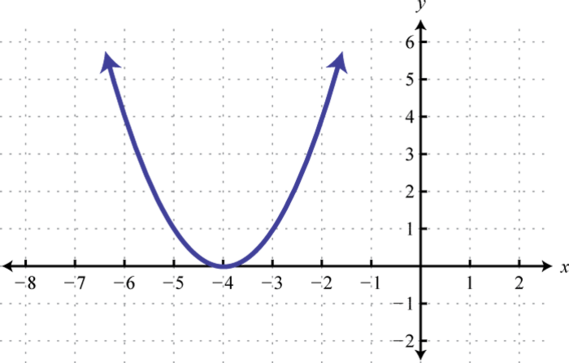
-
;
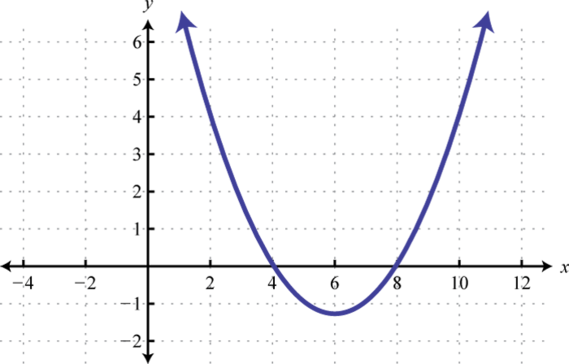
-
;
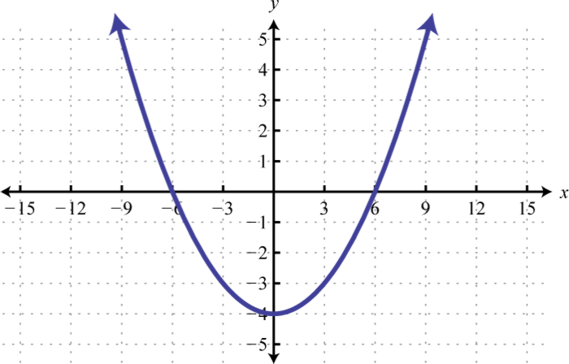
-
;
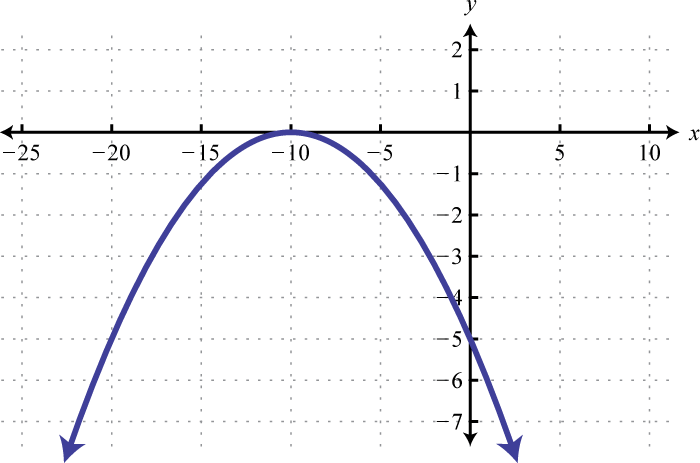
-
;
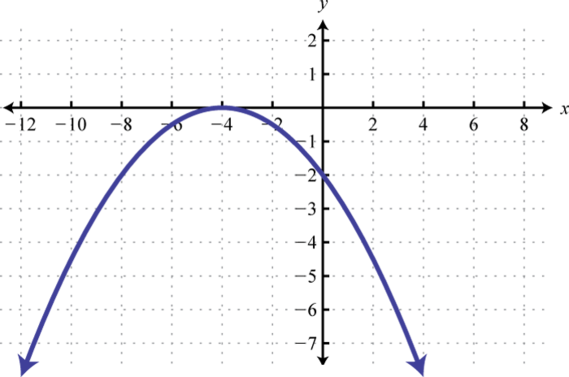
-
-
-
-
-
-
-
-
-
-
Part A: Solutions to Quadratic Inequalities
Determine whether or not the given value is a solution.
Given the graph of f determine the solution set.
Use the transformations to graph the following and then determine the solution set.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
A robotics manufacturing company has determined that its weekly profit in thousands of dollars is modeled by where n represents the number of units it produces and sells. How many units must the company produce and sell to maintain profitability. (Hint: Profitability occurs when profit is greater than zero.)
-
The height in feet of a projectile shot straight into the air is given by where t represents the time in seconds after it is fired. In what time intervals is the projectile under 1,000 feet? Round to the nearest tenth of a second.
Part B: Solving Quadratic Inequalities
Use a sign chart to solve and graph the solution set. Present answers using interval notation.
Find the domain of the function.
-
Does the sign chart for any given quadratic function always alternate? Explain and illustrate your answer with some examples.
-
Research and discuss other methods for solving a quadratic inequality.
-
Explain the difference between a quadratic equation and a quadratic inequality. How can we identify and solve each? What is the geometric interpretation of each?
Part C: Discussion Board
Answers
-
No
-
-
Yes
-
-
No
-
-
Yes
-
-
Yes
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Ø
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
The company must produce and sell more than 10 units and fewer than 20 units each week.
-
-
Answer may vary
-
-
Answer may vary
6.6 Solving Polynomial and Rational Inequalities
Learning Objectives
- Solve polynomial inequalities.
- Solve rational inequalities.
Solving Polynomial Inequalities
A polynomial inequalityA mathematical statement that relates a polynomial expression as either less than or greater than another. is a mathematical statement that relates a polynomial expression as either less than or greater than another. We can use sign charts to solve polynomial inequalities with one variable.
Example 1
Solve:
Solution:
Begin by finding the critical numbers. For a polynomial inequality in standard form, with zero on one side, the critical numbers are the roots. Because is given in its factored form the roots are apparent. Here the roots are: 0, −3, and 4. Because of the strict inequality, plot them using open dots on a number line.
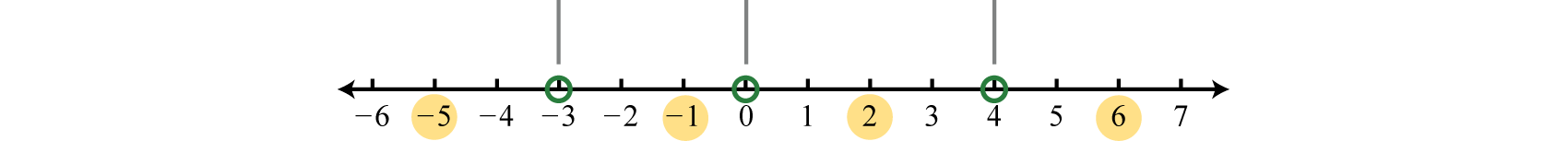
In this case, the critical numbers partition the number line into four regions. Test values in each region to determine if f is positive or negative. Here we choose test values −5, −1, 2, and 6. Remember that we are only concerned with the sign (+ or −) of the result.
After testing values we can complete a sign chart.

The question asks us to find the values where , or where the function is negative. From the sign chart we can see that the function is negative for x-values in between 0 and 4.

We can express this solution set in two ways:
In this textbook we will continue to present solution sets using interval notation.
Answer:
Graphing polynomials such as the one in the previous example is beyond the scope of this textbook. However, the graph of this function is provided below. Compare the graph to its corresponding sign chart.
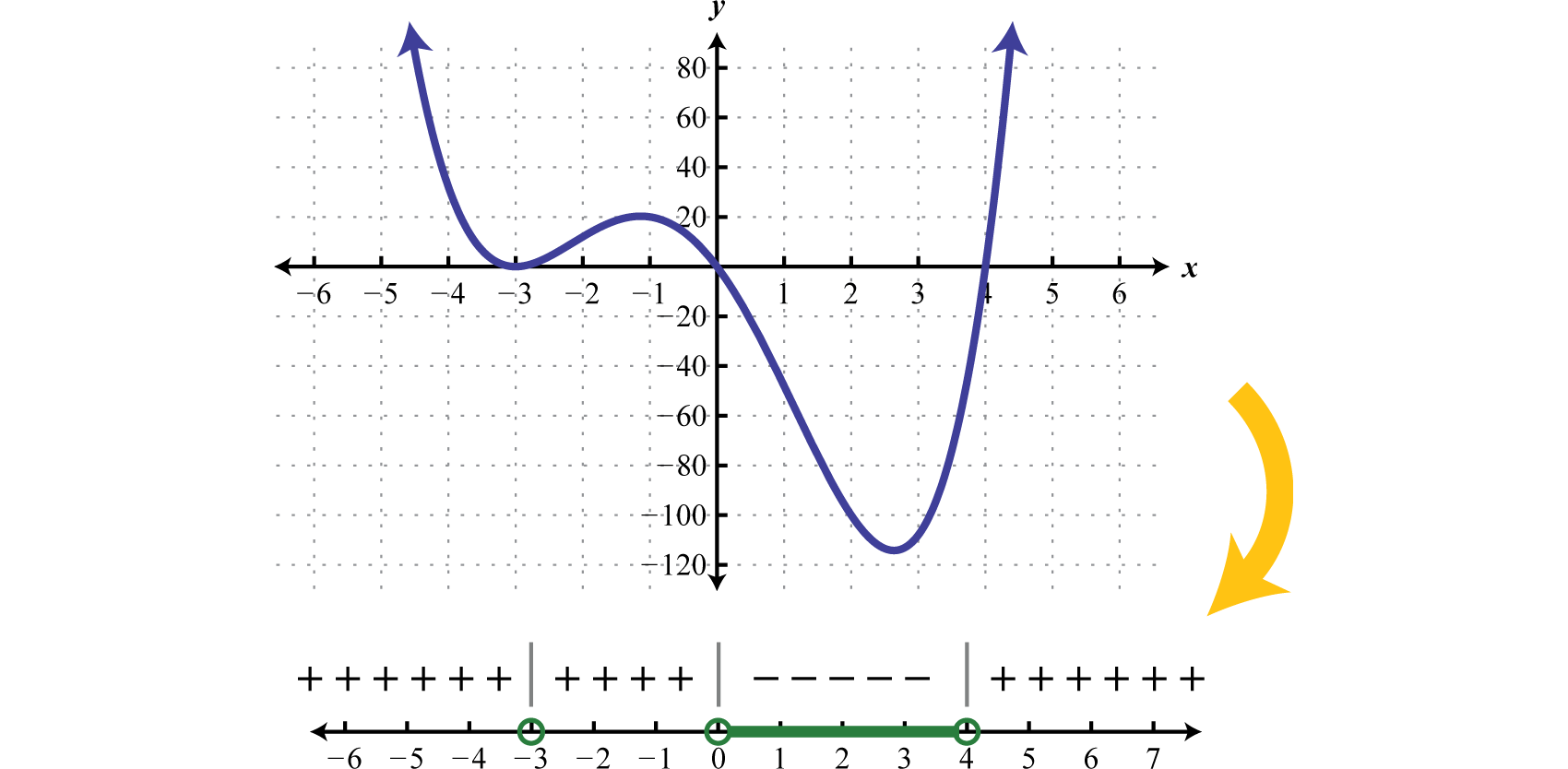
Certainly it may not be the case that the polynomial is factored nor that it has zero on one side of the inequality. To model a function using a sign chart, all of the terms should be on one side and zero on the other. The general steps for solving a polynomial inequality are listed in the following example.
Example 2
Solve:
Solution:
Step 1: Obtain zero on one side of the inequality. In this case, subtract to obtain a polynomial on the left side in standard from.
Step 2: Find the critical numbers. Here we can find the zeros by factoring.
There are three solutions, hence, three critical numbers , 0, and 3.The strict inequality indicates that we should use open dots.

Step 3: Create a sign chart. In this case use and test values −2, −1, 1, and 4 to determine the sign of the function in each interval.
With this information we can complete the sign chart.

Step 4: Use the sign chart to answer the question. Here the solution consists of all values for which Shade in the values that produce positive results and then express this set in interval notation.

Answer:
Example 3
Solve:
Solution:
Begin by rewriting the inequality in standard form, with zero on one side.
Next find the critical numbers of :
The critical numbers are −2, −1, and 2. Because of the inclusive inequality () we will plot them using closed dots.

Use test values −3, , 0, and 3 to create a sign chart.
And we have

Use the sign chart to shade in the values that have negative results ().

Answer:
Solving Rational Inequalities
A rational inequalityA mathematical statement that relates a rational expression as either less than or greater than another. is a mathematical statement that relates a rational expression as either less than or greater than another. Because rational functions have restrictions to the domain we must take care when solving rational inequalities. In addition to the zeros, we will include the restrictions to the domain of the function in the set of critical numbers.
Example 4
Solve:
Solution:
The zeros of a rational function occur when the numerator is zero and the values that produce zero in the denominator are the restrictions. In this case,
Therefore the critical numbers are −2, 1, and 4. Because of the inclusive inequality () use a closed dot for the roots {−2, 4} and always use an open dot for restrictions {1}. Restrictions are never included in the solution set.

Use test values
And then complete the sign chart.

The question asks us to find the values for which , in other words, positive or zero. Shade in the appropriate regions and present the solution set in interval notation.

Answer:
Graphing such rational functions like the one in the previous example is beyond the scope of this textbook. However, the graph of this function is provided below. Compare the graph to its corresponding sign chart.
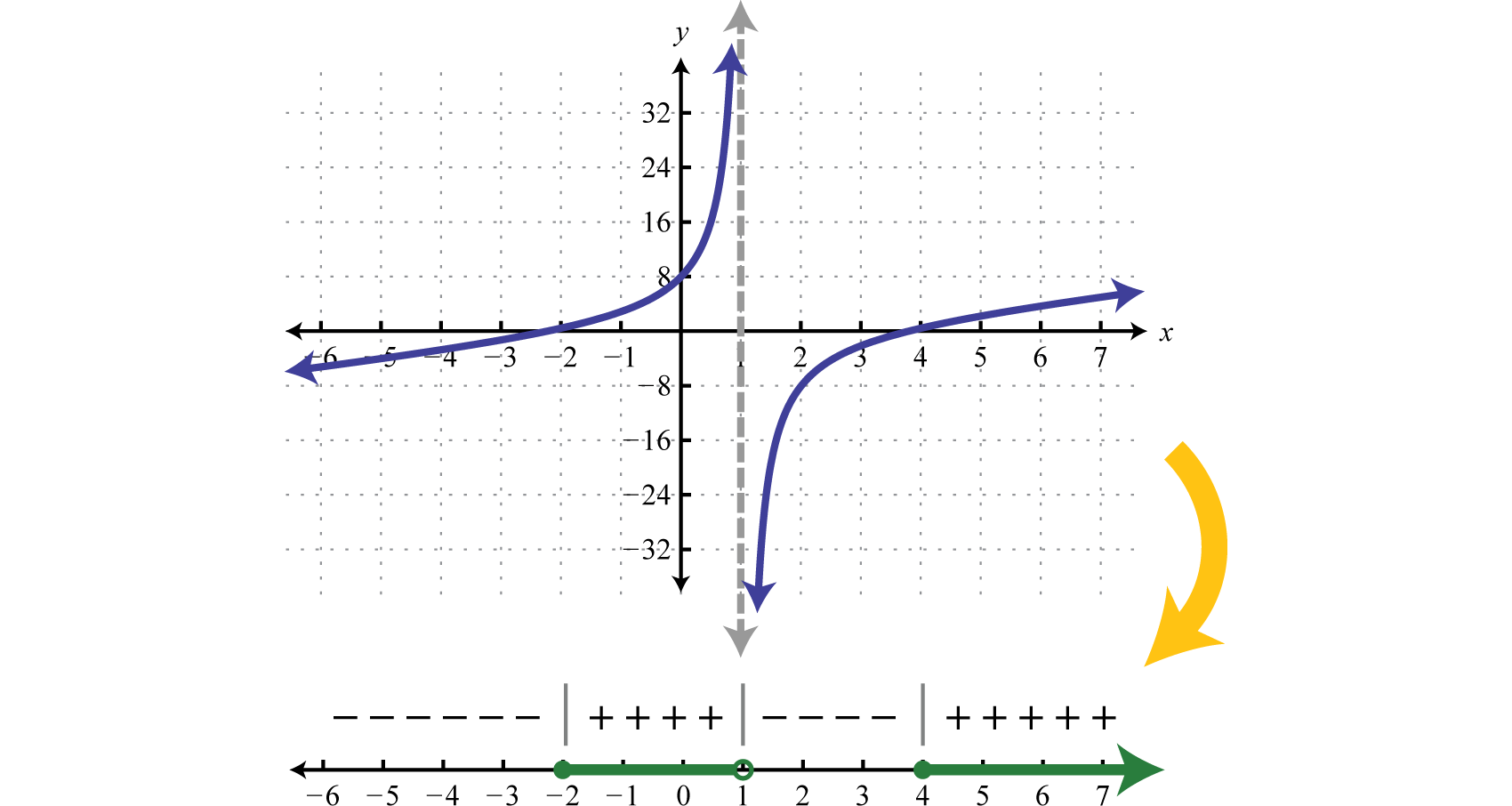
Notice that the restriction corresponds to a vertical asymptote which bounds regions where the function changes from positive to negative. While not included in the solution set, the restriction is a critical number. Before creating a sign chart we must ensure the inequality has a zero on one side. The general steps for solving a rational inequality are outlined in the following example.
Example 5
Solve:
Solution:
Step 1: Begin by obtaining zero on the right side.
Step 2: Determine the critical numbers. The critical numbers are the zeros and restrictions. Begin by simplifying to a single algebraic fraction.
Next find the critical numbers. Set the numerator and denominator equal to zero and solve.
In this case, the strict inequality indicates that we should use an open dot for the root.
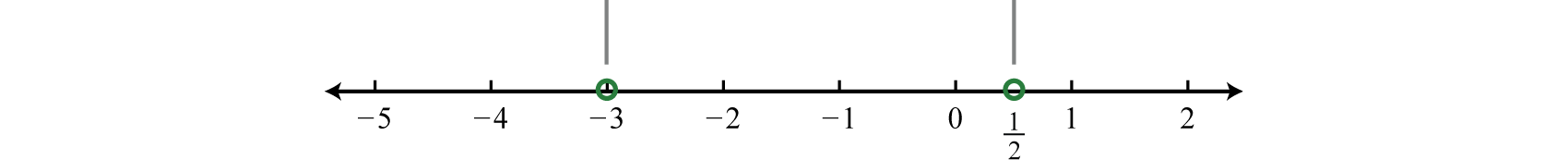
Step 3: Create a sign chart. Choose test values −4, 0, and 1.
And we have
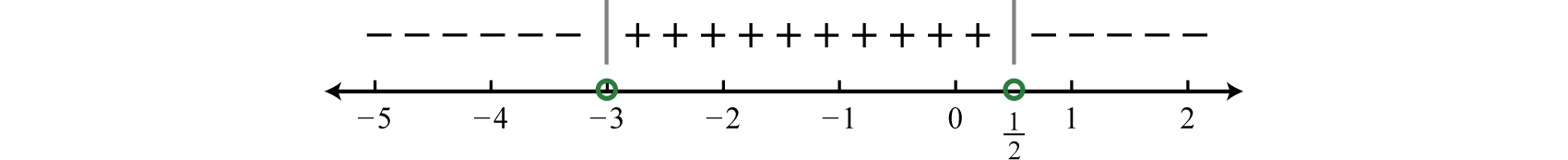
Step 4: Use the sign chart to answer the question. In this example we are looking for the values for which the function is negative, Shade the appropriate values and then present your answer using interval notation.
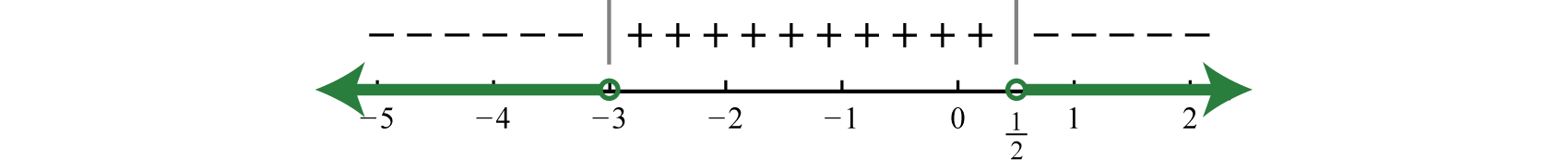
Answer:
Example 6
Solve:
Solution:
Begin by obtaining zero on the right side.
Next simplify the left side to a single algebraic fraction.
The critical numbers are −3, −2, and 2. Note that ±2 are restrictions and thus we will use open dots when plotting them on a number line. Because of the inclusive inequality we will use a closed dot at the root −3.

Choose test values −4, , 0, and 3.
Construct a sign chart.

Answer the question; in this case, find x where

Answer:
Key Takeaways
- When a polynomial inequality is in standard form, with zero on one side, the roots of the polynomial are the critical numbers. Create a sign chart that models the function and then use it to answer the question.
- When a rational inequality is written as a single algebraic fraction, with zero on one side, the roots as well as the restrictions are the critical numbers. The values that produce zero in the numerator are the roots, and the values that produce zero in the denominator are the restrictions. Always use open dots for restrictions, regardless of the given inequality, because restrictions are not part of the domain. Create a sign chart that models the function and then use it to answer the question.
Topic Exercises
Part A: Solving Polynomial Inequalities
Solve. Present answers using interval notation.
Solve.
Part B: Solving Rational Inequalities
Solve.
Solve.
-
Does the sign chart for any given polynomial or rational function always alternate? Explain and illustrate your answer with some examples.
-
Write down your own steps for solving a rational inequality and illustrate them with an example. Do your steps also work for a polynomial inequality? Explain.
Part C: Discussion Board
Answers
-
Answer may vary
-
6.7 Review Exercises and Sample Exam
Review Exercises
-
-
-
-
-
-
-
-
-
-
-
-
-
The height in feet of an object dropped from a 20-foot stepladder is given by where t represents the time in seconds after the object has been dropped. How long does it take the object to hit the ground after it has been dropped? Round to the nearest tenth of a second.
-
A 20-foot ladder, leaning against a building, reaches a height of 19 feet. How far is the base of the ladder from the wall? Round to the nearest tenth of a foot.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Extracting Square Roots and Completing the Square
Solve by extracting the roots.
Solve by completing the square.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
The height in feet of a baseball tossed upward at a speed of 48 feet per second from the ground is given by the function, , where t represents the time in seconds after the ball is tossed. At what time does the baseball reach a height of 18 feet? Round off to the nearest hundredth of a second.
-
The height in feet reached by a model rocket launched from a 3-foot platform is given by the function where t represents time in seconds after launch. At what times will the rocket reach 1,000 feet? Round off to the nearest tenth of a second.
-
-
-
-
Quadratic Formula
Solve using the quadratic formula.
Use the discriminant to determine the number and type of solutions.
-
-
-
-
-
-
-
-
-
-
-
The length of a rectangle is 3 inches less than twice the width. If the area of the rectangle measures 30 square inches, then find the dimensions of the rectangle. Round off to the nearest hundredth of an inch.
-
The value in dollars of a new car is modeled by the function where t represents the number of years since it was purchased. Determine the age of the car when its value is $18,000.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Solving Equations Quadratic in Form
Solve using any method.
Find all solutions.
Find the set of all roots.
Find a quadratic equation with integer coefficients and the given set of solutions.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
The value in dollars of a new car is modeled by where t represents the number of years since it was purchased. Determine the age of the car when its value is at a minimum.
-
The height in feet of a baseball tossed upward at a speed of 48 feet per second from the ground is given by the function, , where t represents the time in seconds after it is tossed. What is the maximum height of the baseball?
-
The rectangular area in square feet that can be enclosed with 200 feet of fencing is given by where w represents the width of the rectangular area in feet. What dimensions will maximize the area that can be enclosed?
-
A manufacturing company has found that production costs in thousands of dollars are modeled by where x represents the number of employees. Determine the number of employees that will minimize production costs.
Quadratic Functions and Their Graphs
Determine the x- and y-intercepts.
Find the vertex and the line of symmetry.
Graph. Find the vertex and the y-intercept. In addition, find the x-intercepts if they exist.
Determine the maximum or minimum y-value.
Rewrite in vertex form and determine the vertex.
Graph. Find the vertex and the y-intercept. In addition, find the x-intercepts if they exist.
Solving Quadratic Inequalities
Solve. Present answers using interval notation.
Find the domain of the function.
Solving Polynomial and Rational Inequalities
Solve. Present answers using interval notation.
Answers
-
±9
-
-
-
-
-
-
,
-
-
-
-
-
-
seconds
-
-
−5,1
-
-
-
-
-
-
−2, 1
-
-
-
-
-
-
-
-
-
-
, 2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
,
-
-
−1, 0
-
-
The ball will reach 18 feet at 0.44 seconds and again at 2.56 seconds.
-
-
Two irrational solutions
-
-
One rational solution
-
-
−8, 12
-
-
-
-
-
-
-
-
−4, −1
-
-
Length: 6.38 inches; width: 4.69 inches
-
-
,
-
-
,
-
-
16
-
-
−3,
-
-
1,
-
-
,
-
-
-
-
-
-
-
-
-
-
-
-
x-intercepts: (−4, 0), ; y-intercept: (0, −12)
-
-
x-intercepts: none; y-intercept: (0, 7)
-
-
Vertex: (2, −16); line of symmetry:
-
-
Vertex: ; line of symmetry:
-
-
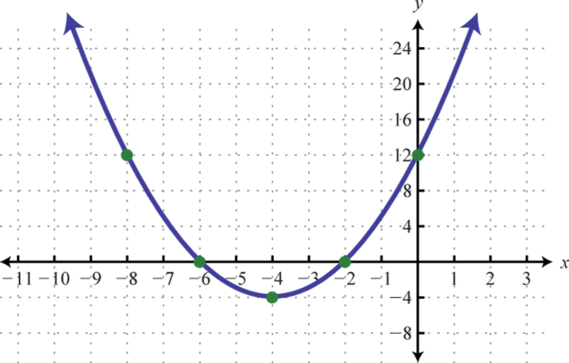
-
-
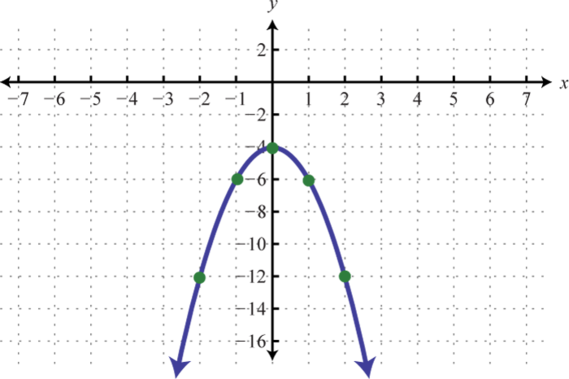
-
-
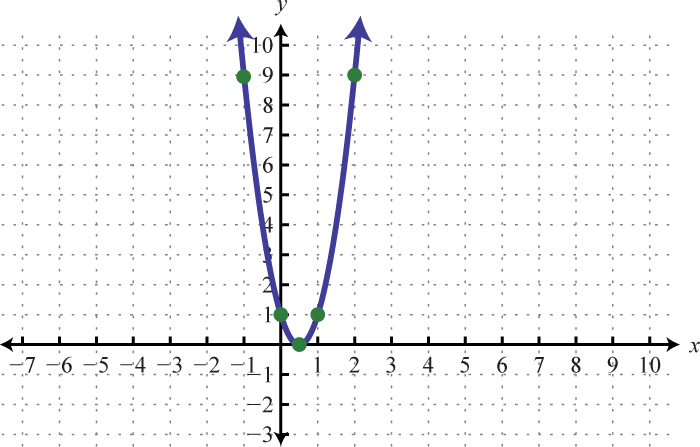
-
-
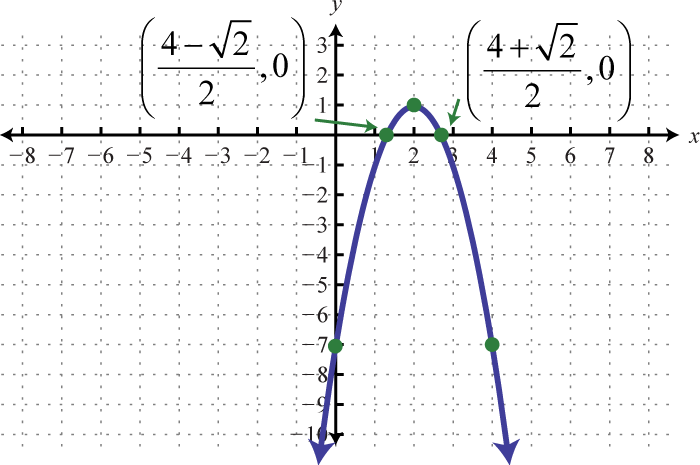
-
-
Minimum:
-
-
Maximum:
-
-
; vertex:
-
-
; vertex:
-
-
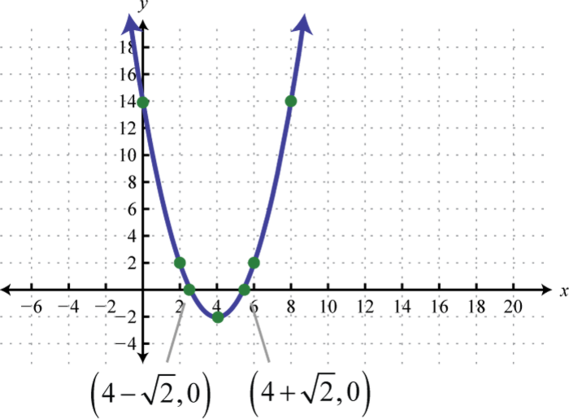
-
-
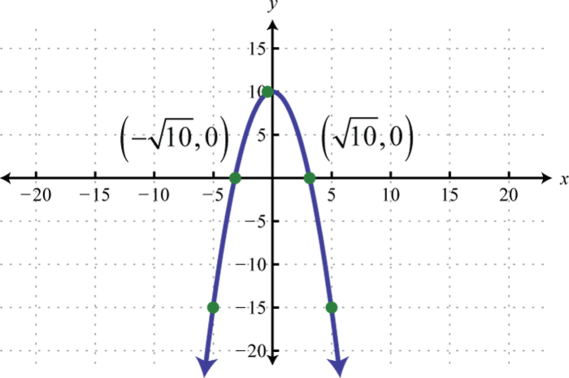
-
-
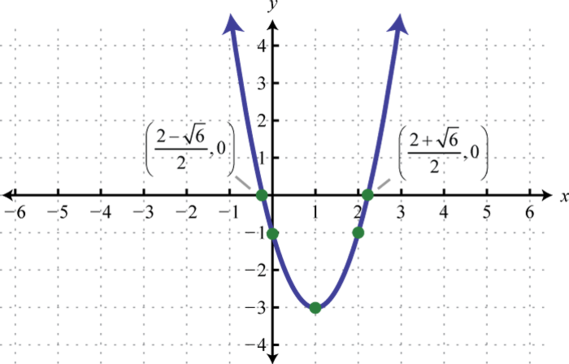
-
-
The car will have minimum value 12 years after it is purchased.
-
-
Length: 50 feet; width: 50 feet
-
-
-
-
-
-
-
-
-
-
Ø
-
-
-
-
-
-
-
-
-
Sample Exam
-
Solve by extracting the roots:
-
Solve by completing the square:
-
-
-
-
-
Find a quadratic equation with integer coefficients and solutions
-
The area of a rectangle is 22 square centimeters. If the length is 5 centimeters less than twice the width, then find the dimensions of the rectangle. Round off to the nearest tenth of a centimeter.
-
Assuming dry road conditions and average reaction times, the safe stopping distance in feet of a certain car is given by where x represents the speed of the car in miles per hour. Determine the safe speed of the car if you expect to stop in 100 feet. Round off to the nearest mile per hour.
-
-
-
-
-
-
-
-
Given the function defined by :
- Does the function have a minimum or maximum? Explain.
- Find the minimum or maximum y-value.
-
The height in feet of a water rocket launched from the ground is given by the function where t represents the number of seconds after launch. What is the maximum height attained by the rocket?
-
Graph and find x where
-
Graph and find x where
-
-
-
-
-
Solve using the quadratic formula.
Find all solutions.
Graph. Find the vertex and the y-intercept. In addition, find the x-intercepts if they exist.
Sketch the graph and use it to solve the given inequality.
Solve. Present answers using interval notation.
Answers
-
-
-
-
-
-
-
-
-
36 miles per hour
-
-
−3,
-
-
16
-
-
-
-
- Minimum
-
-
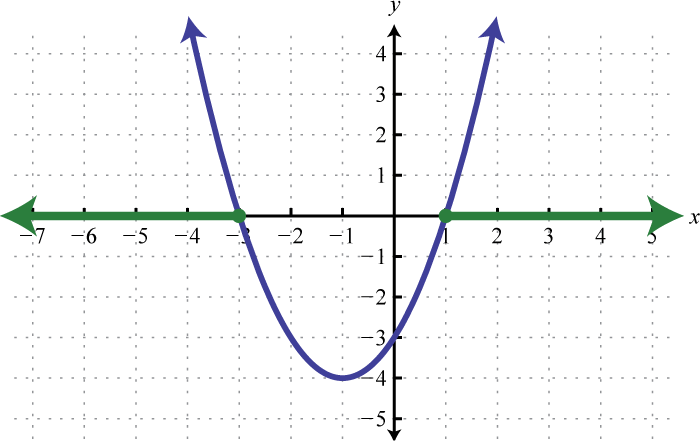
-
-
-
-
-
-