This is “Review Exercises and Sample Exam”, section 6.7 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
6.7 Review Exercises and Sample Exam
Review Exercises
-
-
-
-
-
-
-
-
-
-
-
-
-
The height in feet of an object dropped from a 20-foot stepladder is given by where t represents the time in seconds after the object has been dropped. How long does it take the object to hit the ground after it has been dropped? Round to the nearest tenth of a second.
-
A 20-foot ladder, leaning against a building, reaches a height of 19 feet. How far is the base of the ladder from the wall? Round to the nearest tenth of a foot.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Extracting Square Roots and Completing the Square
Solve by extracting the roots.
Solve by completing the square.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
The height in feet of a baseball tossed upward at a speed of 48 feet per second from the ground is given by the function, , where t represents the time in seconds after the ball is tossed. At what time does the baseball reach a height of 18 feet? Round off to the nearest hundredth of a second.
-
The height in feet reached by a model rocket launched from a 3-foot platform is given by the function where t represents time in seconds after launch. At what times will the rocket reach 1,000 feet? Round off to the nearest tenth of a second.
-
-
-
-
Quadratic Formula
Solve using the quadratic formula.
Use the discriminant to determine the number and type of solutions.
-
-
-
-
-
-
-
-
-
-
-
The length of a rectangle is 3 inches less than twice the width. If the area of the rectangle measures 30 square inches, then find the dimensions of the rectangle. Round off to the nearest hundredth of an inch.
-
The value in dollars of a new car is modeled by the function where t represents the number of years since it was purchased. Determine the age of the car when its value is $18,000.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Solving Equations Quadratic in Form
Solve using any method.
Find all solutions.
Find the set of all roots.
Find a quadratic equation with integer coefficients and the given set of solutions.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
The value in dollars of a new car is modeled by where t represents the number of years since it was purchased. Determine the age of the car when its value is at a minimum.
-
The height in feet of a baseball tossed upward at a speed of 48 feet per second from the ground is given by the function, , where t represents the time in seconds after it is tossed. What is the maximum height of the baseball?
-
The rectangular area in square feet that can be enclosed with 200 feet of fencing is given by where w represents the width of the rectangular area in feet. What dimensions will maximize the area that can be enclosed?
-
A manufacturing company has found that production costs in thousands of dollars are modeled by where x represents the number of employees. Determine the number of employees that will minimize production costs.
Quadratic Functions and Their Graphs
Determine the x- and y-intercepts.
Find the vertex and the line of symmetry.
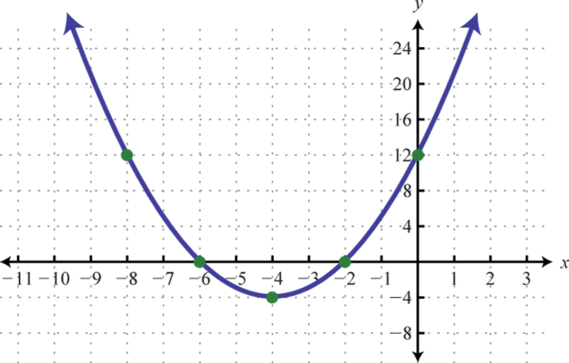
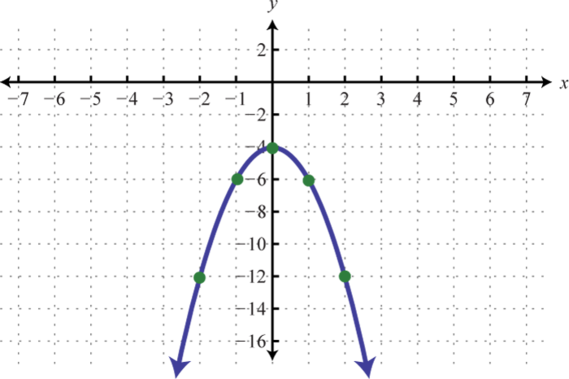
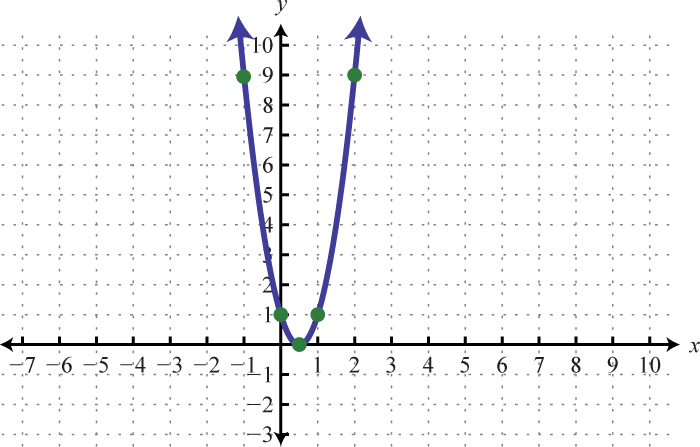
Graph. Find the vertex and the y-intercept. In addition, find the x-intercepts if they exist.
Determine the maximum or minimum y-value.
Rewrite in vertex form and determine the vertex.
Graph. Find the vertex and the y-intercept. In addition, find the x-intercepts if they exist.
Solving Quadratic Inequalities
Solve. Present answers using interval notation.
Find the domain of the function.
Solving Polynomial and Rational Inequalities
Solve. Present answers using interval notation.
Answers
-
±9
-
-
-
-
-
-
,
-
-
-
-
-
-
seconds
-
-
−5,1
-
-
-
-
-
-
−2, 1
-
-
-
-
-
-
-
-
-
-
, 2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
,
-
-
−1, 0
-
-
The ball will reach 18 feet at 0.44 seconds and again at 2.56 seconds.
-
-
Two irrational solutions
-
-
One rational solution
-
-
−8, 12
-
-
-
-
-
-
-
-
−4, −1
-
-
Length: 6.38 inches; width: 4.69 inches
-
-
,
-
-
,
-
-
16
-
-
−3,
-
-
1,
-
-
,
-
-
-
-
-
-
-
-
-
-
-
-
x-intercepts: (−4, 0), ; y-intercept: (0, −12)
-
-
x-intercepts: none; y-intercept: (0, 7)
-
-
Vertex: (2, −16); line of symmetry:
-
-
Vertex: ; line of symmetry:
-
-
-
-
-
-
-
-
-
-
Minimum:
-
-
Maximum:
-
-
; vertex:
-
-
; vertex:
-
-
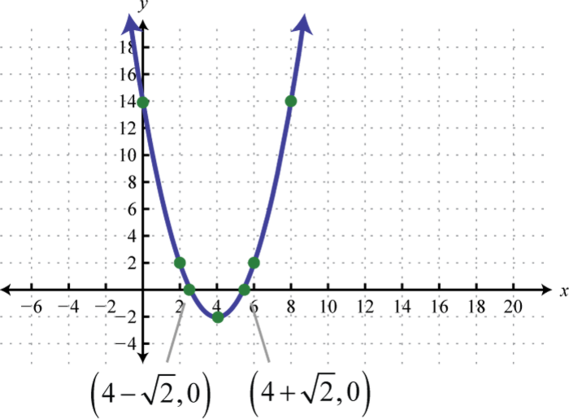
-
-
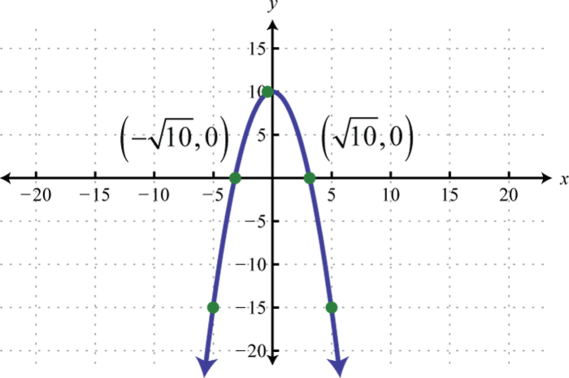
-
-
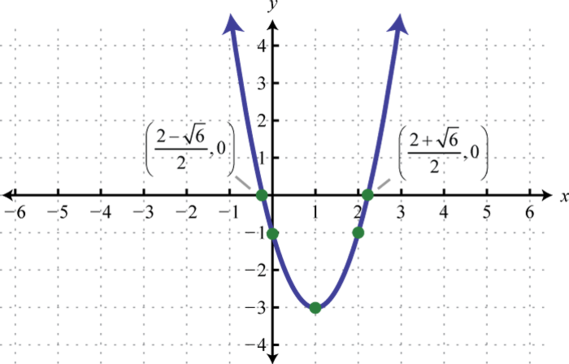
-
-
The car will have minimum value 12 years after it is purchased.
-
-
Length: 50 feet; width: 50 feet
-
-
-
-
-
-
-
-
-
-
Ø
-
-
-
-
-
-
-
-
-
Sample Exam
-
Solve by extracting the roots:
-
Solve by completing the square:
-
-
-
-
-
Find a quadratic equation with integer coefficients and solutions
-
The area of a rectangle is 22 square centimeters. If the length is 5 centimeters less than twice the width, then find the dimensions of the rectangle. Round off to the nearest tenth of a centimeter.
-
Assuming dry road conditions and average reaction times, the safe stopping distance in feet of a certain car is given by where x represents the speed of the car in miles per hour. Determine the safe speed of the car if you expect to stop in 100 feet. Round off to the nearest mile per hour.
-
-
-
-
-
-
-
-
Given the function defined by :
- Does the function have a minimum or maximum? Explain.
- Find the minimum or maximum y-value.
-
The height in feet of a water rocket launched from the ground is given by the function where t represents the number of seconds after launch. What is the maximum height attained by the rocket?
-
Graph and find x where
-
Graph and find x where
-
-
-
-
-
Solve using the quadratic formula.
Find all solutions.
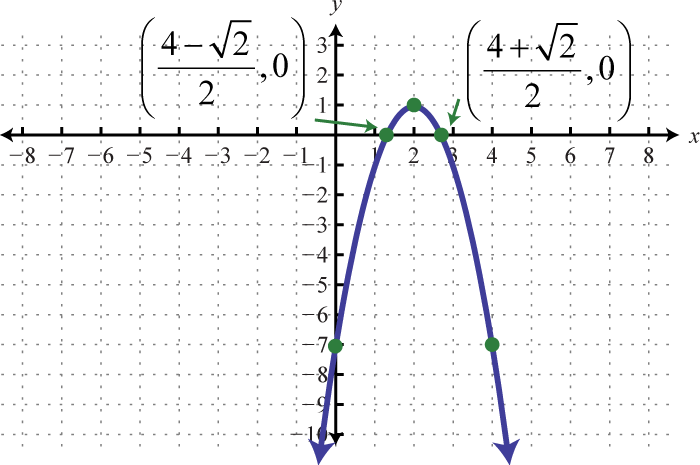
Graph. Find the vertex and the y-intercept. In addition, find the x-intercepts if they exist.
Sketch the graph and use it to solve the given inequality.
Solve. Present answers using interval notation.
Answers
-
-
-
-
-
-
-
-
-
36 miles per hour
-
-
−3,
-
-
16
-
-
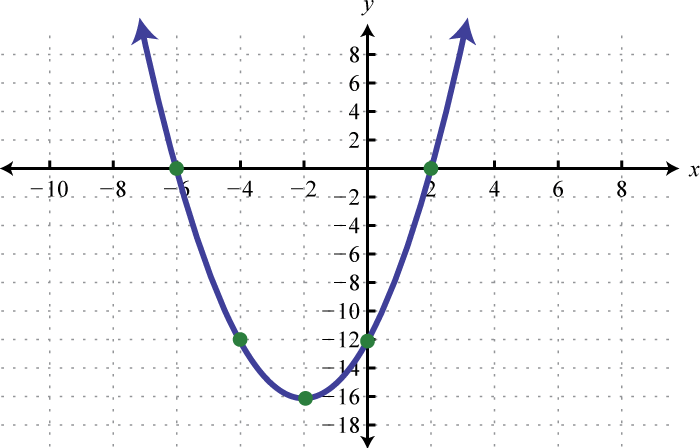
-
-
- Minimum
-
-
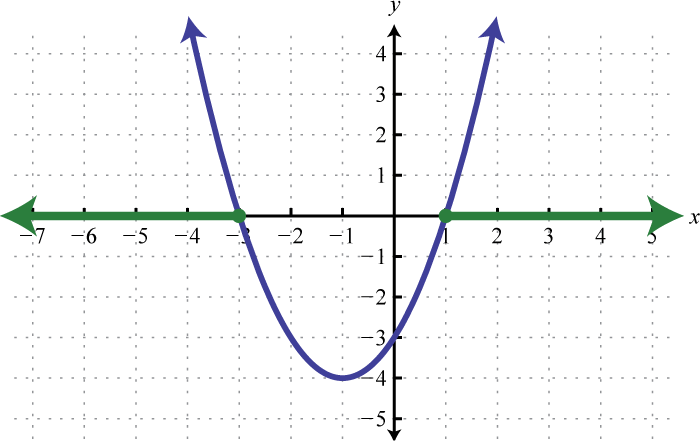
-
-
-
-
-
-




