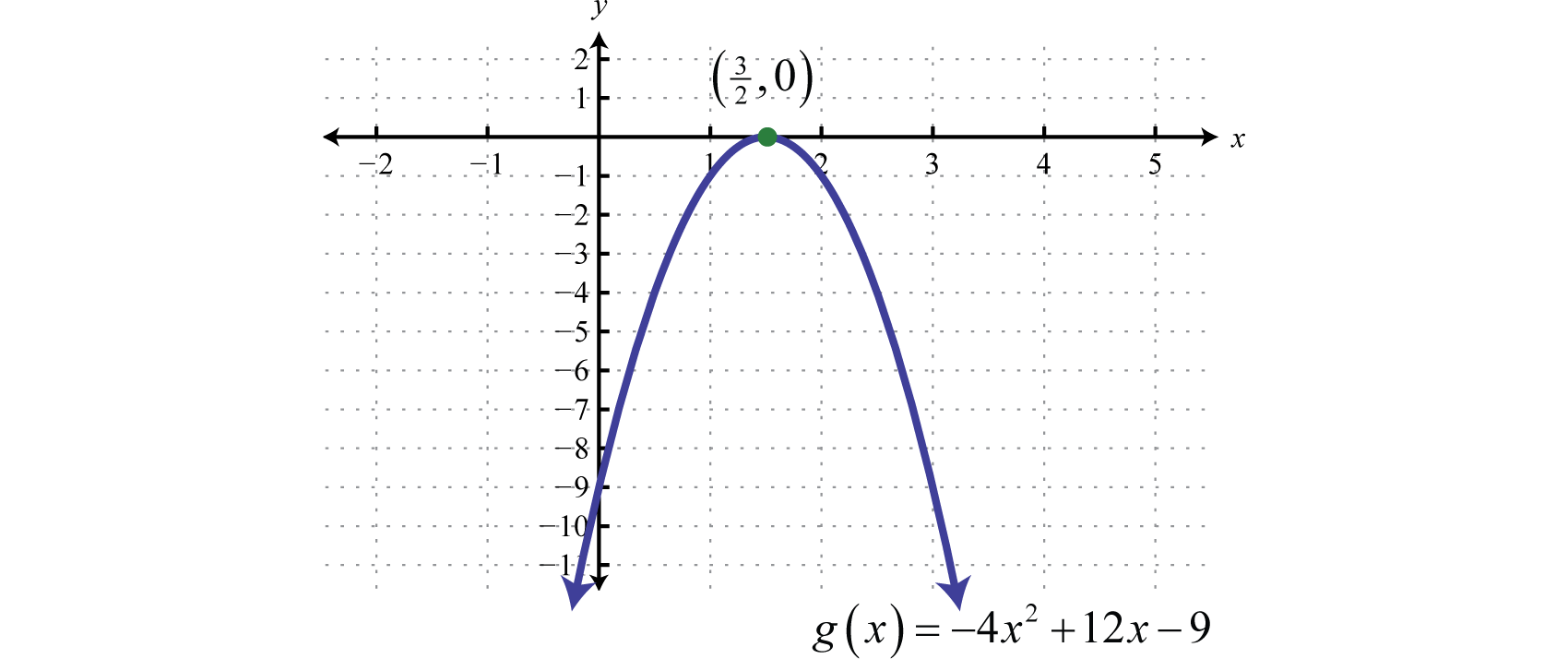
This is “Quadratic Functions and Their Graphs”, section 6.4 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
6.4 Quadratic Functions and Their Graphs
Learning Objectives
- Graph a parabola.
- Find the intercepts and vertex of a parabola.
- Find the maximum and minimum y-value.
- Find the vertex of a parabola by completing the square.
The Graph of a Quadratic Function
A quadratic function is a polynomial function of degree 2 which can be written in the general form,
Here a, b and c represent real numbers where The squaring function is a quadratic function whose graph follows.
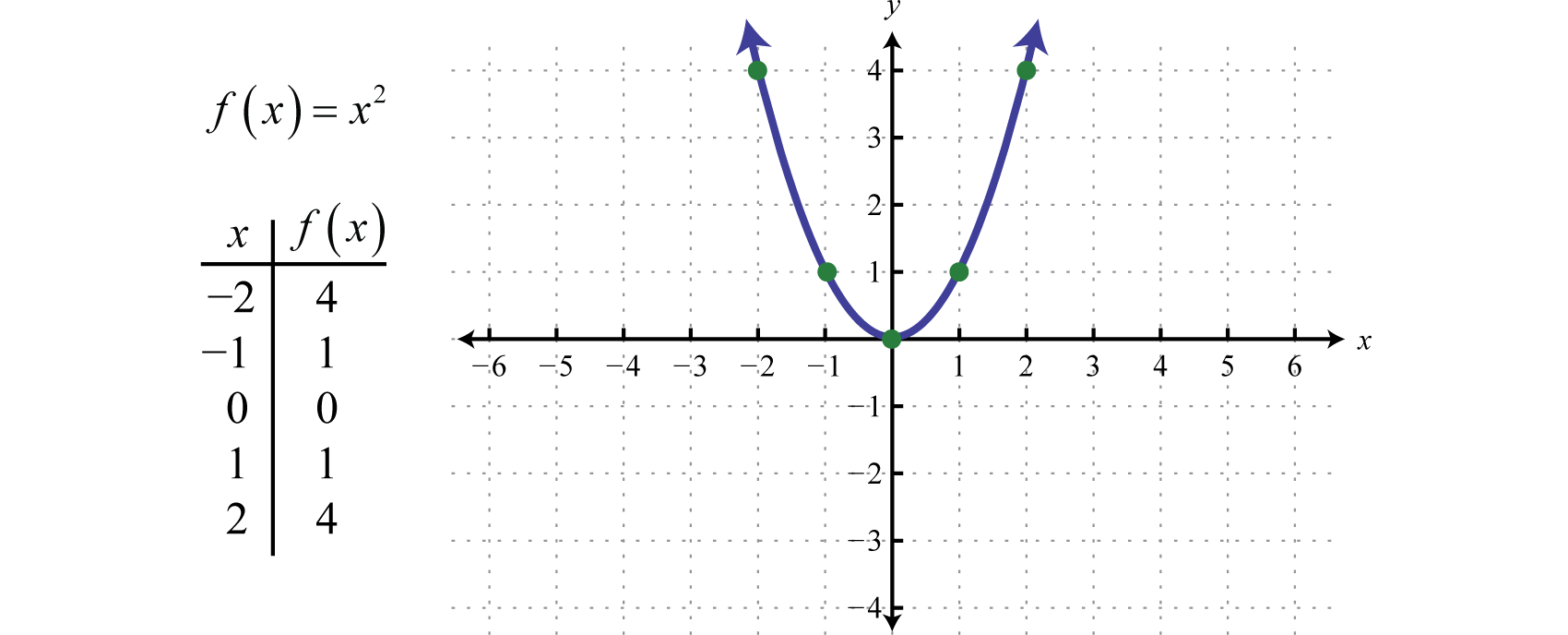
This general curved shape is called a parabolaThe U-shaped graph of any quadratic function defined by , where a, b, and c are real numbers and and is shared by the graphs of all quadratic functions. Note that the graph is indeed a function as it passes the vertical line test. Furthermore, the domain of this function consists of the set of all real numbers and the range consists of the set of nonnegative numbers
When graphing parabolas, we want to include certain special points in the graph. The y-intercept is the point where the graph intersects the y-axis. The x-intercepts are the points where the graph intersects the x-axis. The vertexThe point that defines the minimum or maximum of a parabola. is the point that defines the minimum or maximum of the graph. Lastly, the line of symmetryThe vertical line through the vertex, , about which the parabola is symmetric. (also called the axis of symmetryA term used when referencing the line of symmetry.) is the vertical line through the vertex, about which the parabola is symmetric.
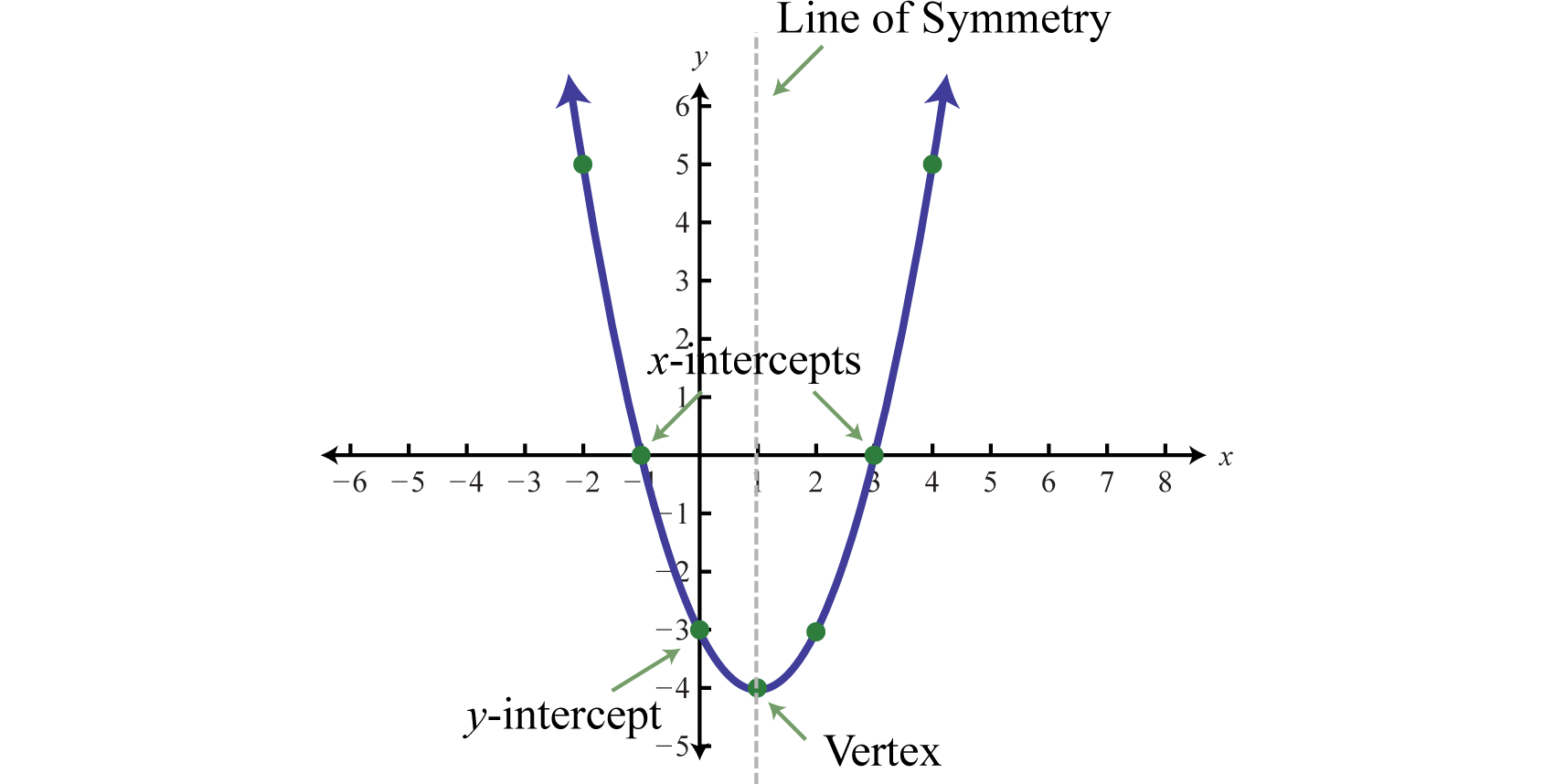
For any parabola, we will find the vertex and y-intercept. In addition, if the x-intercepts exist, then we will want to determine those as well. Guessing at the x-values of these special points is not practical; therefore, we will develop techniques that will facilitate finding them. Many of these techniques will be used extensively as we progress in our study of algebra.
Given a quadratic function , find the y-intercept by evaluating the function where In general, , and we have
Next, recall that the x-intercepts, if they exist, can be found by setting Doing this, we have , which has general solutions given by the quadratic formula, Therefore, the x-intercepts have this general form:
Using the fact that a parabola is symmetric, we can determine the vertical line of symmetry using the x-intercepts. To do this, we find the x-value midway between the x-intercepts by taking an average as follows:
Therefore, the line of symmetry is the vertical line We can use the line of symmetry to find the the vertex.
Generally three points determine a parabola. However, in this section we will find five points so that we can get a better approximation of the general shape. The steps for graphing a parabola are outlined in the following example.
Example 1
Graph:
Solution:
Step 1: Determine the y-intercept. To do this, set and find
The y-intercept is
Step 2: Determine the x-intercepts if any. To do this, set and solve for x.
Here where , we obtain two solutions. Hence, there are two x-intercepts, and
Step 3: Determine the vertex. One way to do this is to first use to find the x-value of the vertex and then substitute this value in the function to find the corresponding y-value. In this example, and
Substitute −1 into the original function to find the corresponding y-value.
The vertex is
Step 4: Determine extra points so that we have at least five points to plot. Ensure a good sampling on either side of the line of symmetry. In this example, one other point will suffice. Choose and find the corresponding y-value.
Our fifth point is
Step 5: Plot the points and sketch the graph. To recap, the points that we have found are
Answer:
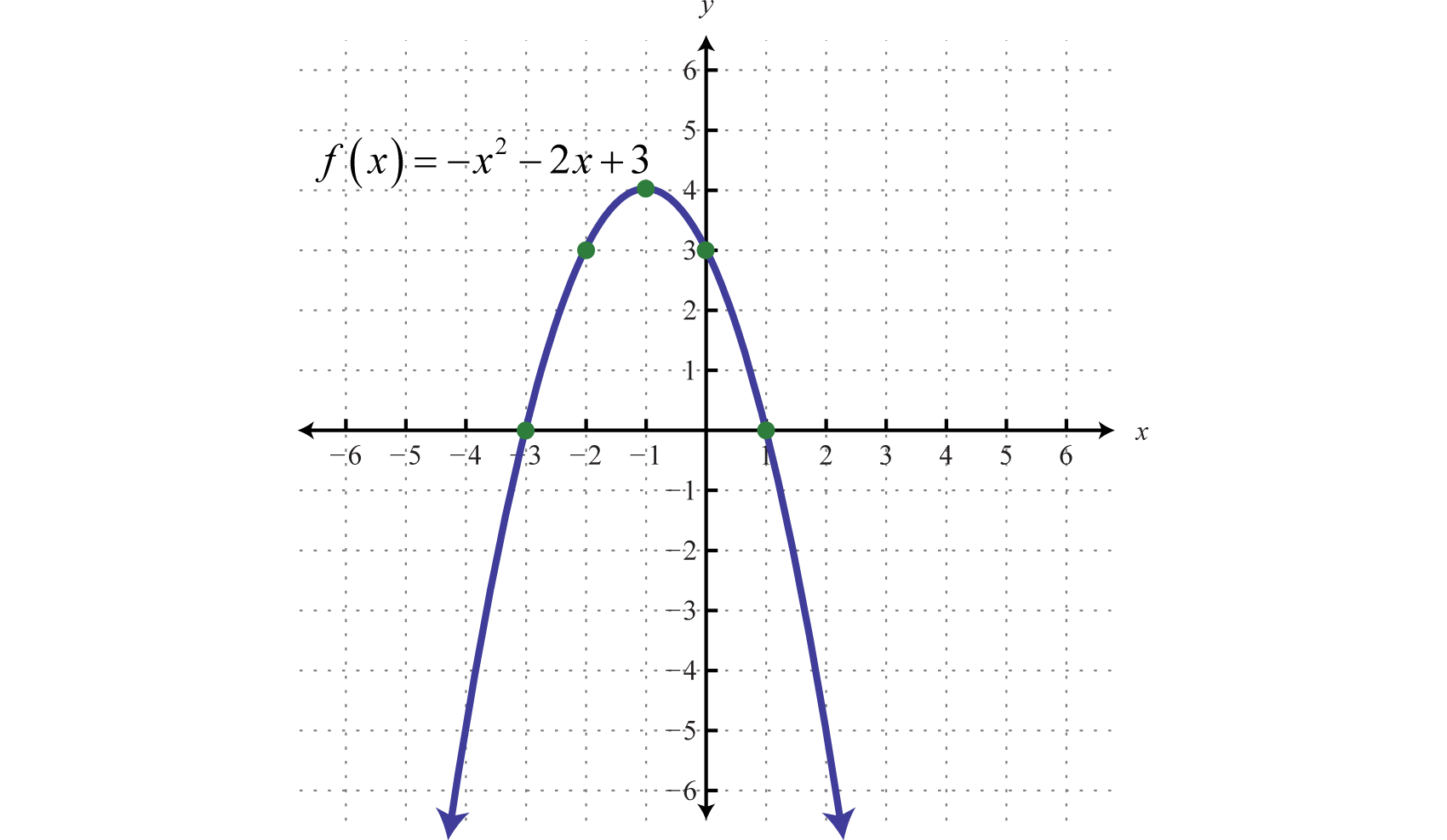
The parabola opens downward. In general, use the leading coefficient to determine if the parabola opens upward or downward. If the leading coefficient is negative, as in the previous example, then the parabola opens downward. If the leading coefficient is positive, then the parabola opens upward.
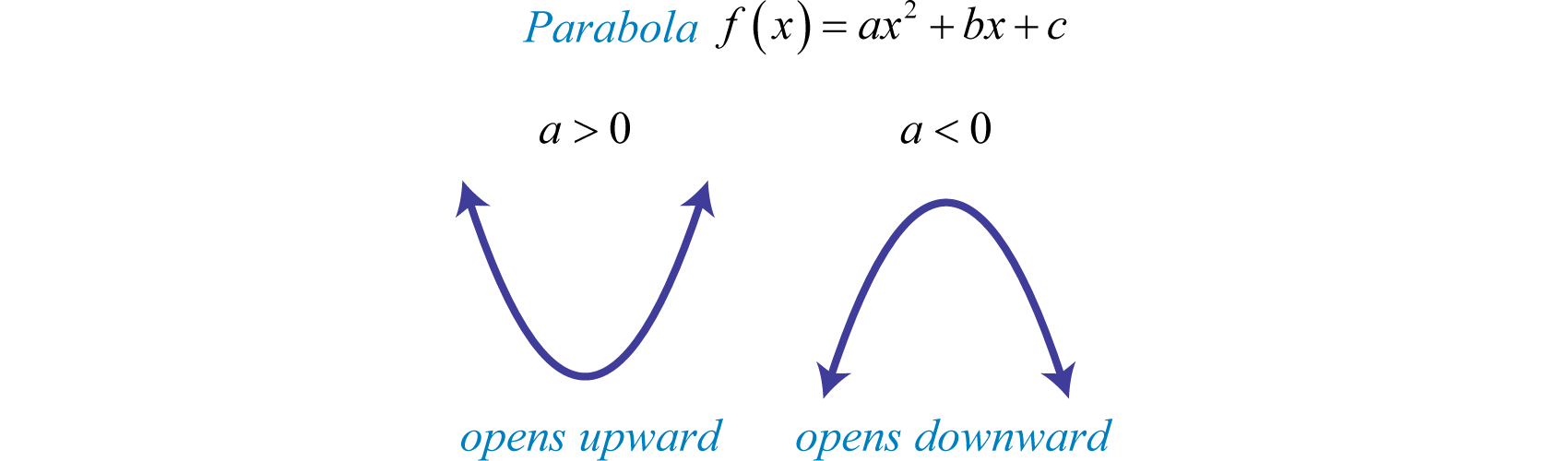
All quadratic functions of the form have parabolic graphs with y-intercept However, not all parabolas have x-intercepts.
Example 2
Graph:
Solution:
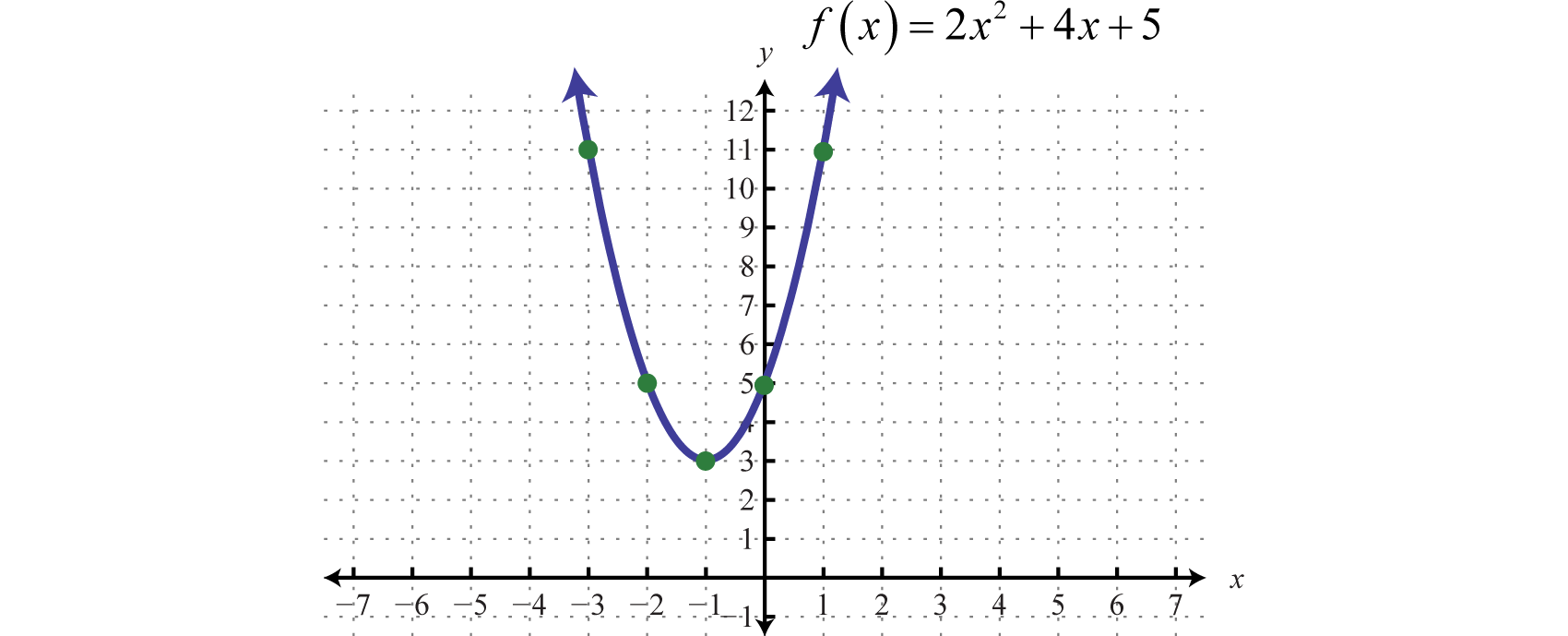
Because the leading coefficient 2 is positive, we note that the parabola opens upward. Here c = 5 and the y-intercept is (0, 5). To find the x-intercepts, set
In this case, a = 2, b = 4, and c = 5. Use the discriminant to determine the number and type of solutions.
Since the discriminant is negative, we conclude that there are no real solutions. Because there are no real solutions, there are no x-intercepts. Next, we determine the x-value of the vertex.
Given that the x-value of the vertex is −1, substitute −1 into the original equation to find the corresponding y-value.
The vertex is (−1, 3). So far, we have only two points. To determine three more, choose some x-values on either side of the line of symmetry, x = −1. Here we choose x-values −3, −2, and 1.
To summarize, we have
Plot the points and sketch the graph.
Answer:
Example 3
Graph:
Solution:
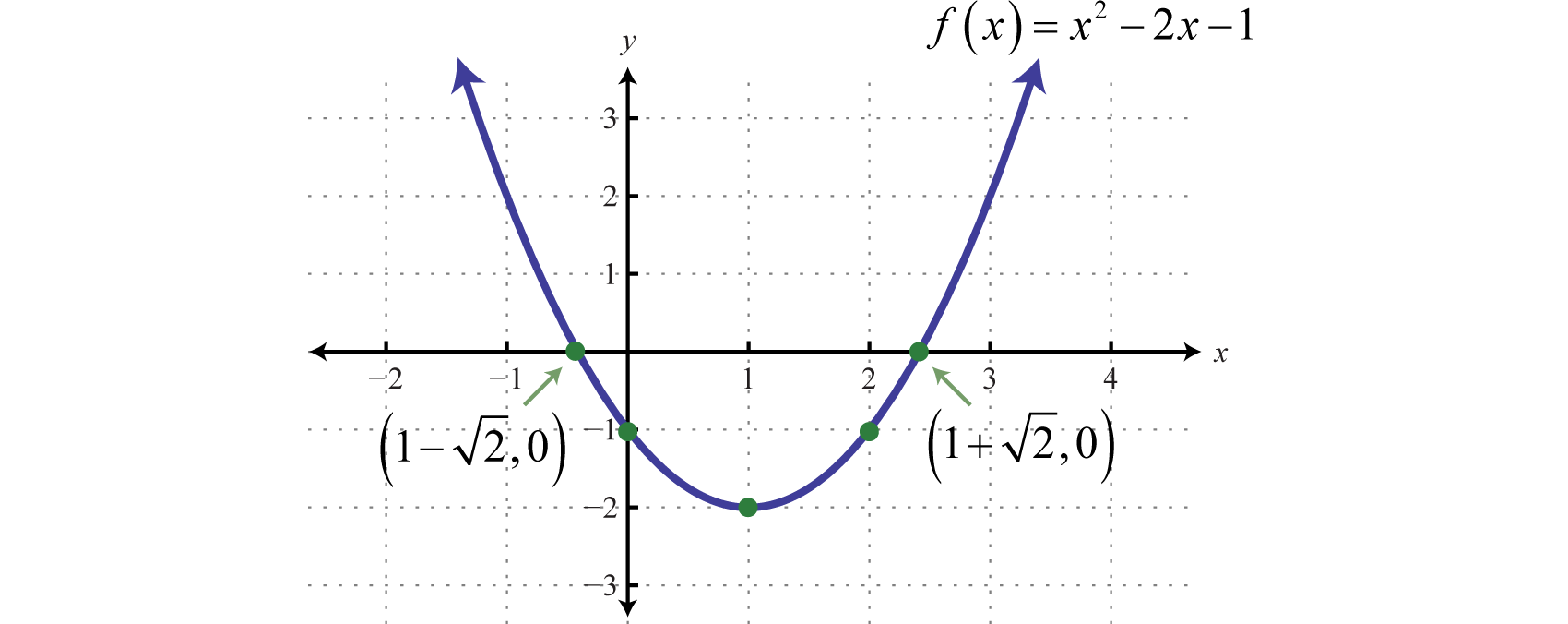
Since a = 1, the parabola opens upward. Furthermore, c = −1, so the y-intercept is To find the x-intercepts, set
In this case, solve using the quadratic formula with a = 1, b = −2, and c = −1.
Here we obtain two real solutions for x, and thus there are two x-intercepts:
Approximating the x-intercepts using a calculator will help us plot the points. However, we will present the exact x-intercepts on the graph. Next, find the vertex.
Given that the x-value of the vertex is 1, substitute into the original equation to find the corresponding y-value.
The vertex is (1, −2). We need one more point.
To summarize, we have
Plot the points and sketch the graph.
Answer:
Finding the Maximum or Minimum
It is often useful to find the maximum and/or minimum values of functions that model real-life applications. To find these important values given a quadratic function, we use the vertex. If the leading coefficient a is positive, then the parabola opens upward and there will be a minimum y-value. If the leading coefficient a is negative, then the parabola opens downward and there will be a maximum y-value.
Example 4
Determine the maximum or minimum:
Solution:
Since a = −4, we know that the parabola opens downward and there will be a maximum y-value. To find it, first find the x-value of the vertex.
The x-value of the vertex is 3. Substitute this value into the original equation to find the corresponding y-value.
The vertex is (3, 1). Therefore, the maximum y-value is 1, which occurs where x = 3, as illustrated below:
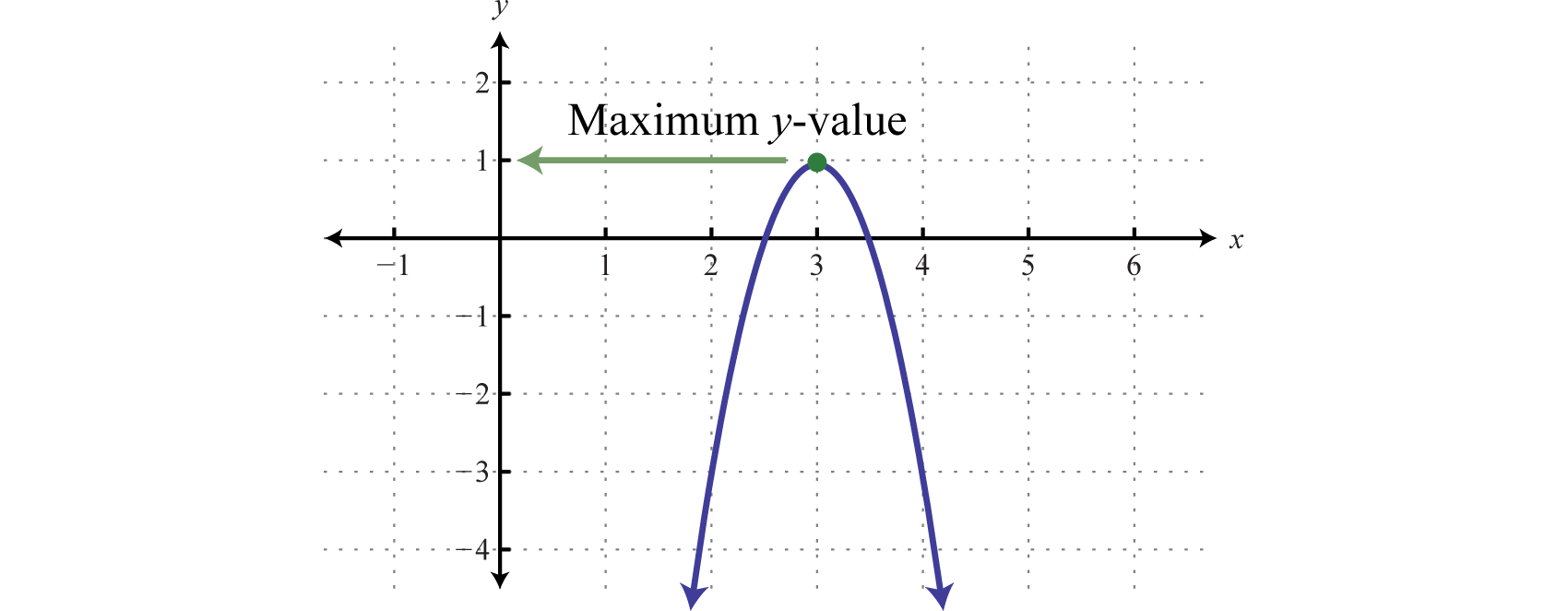
Note: The graph is not required to answer this question.
Answer: The maximum is 1.
Example 5
Determine the maximum or minimum:
Solution:
Since a = 4, the parabola opens upward and there is a minimum y-value. Begin by finding the x-value of the vertex.
Substitute x = 4 into the original equation to find the corresponding y-value.
The vertex is (4, −2). Therefore, the minimum y-value of −2 occurs where x = 4, as illustrated below:
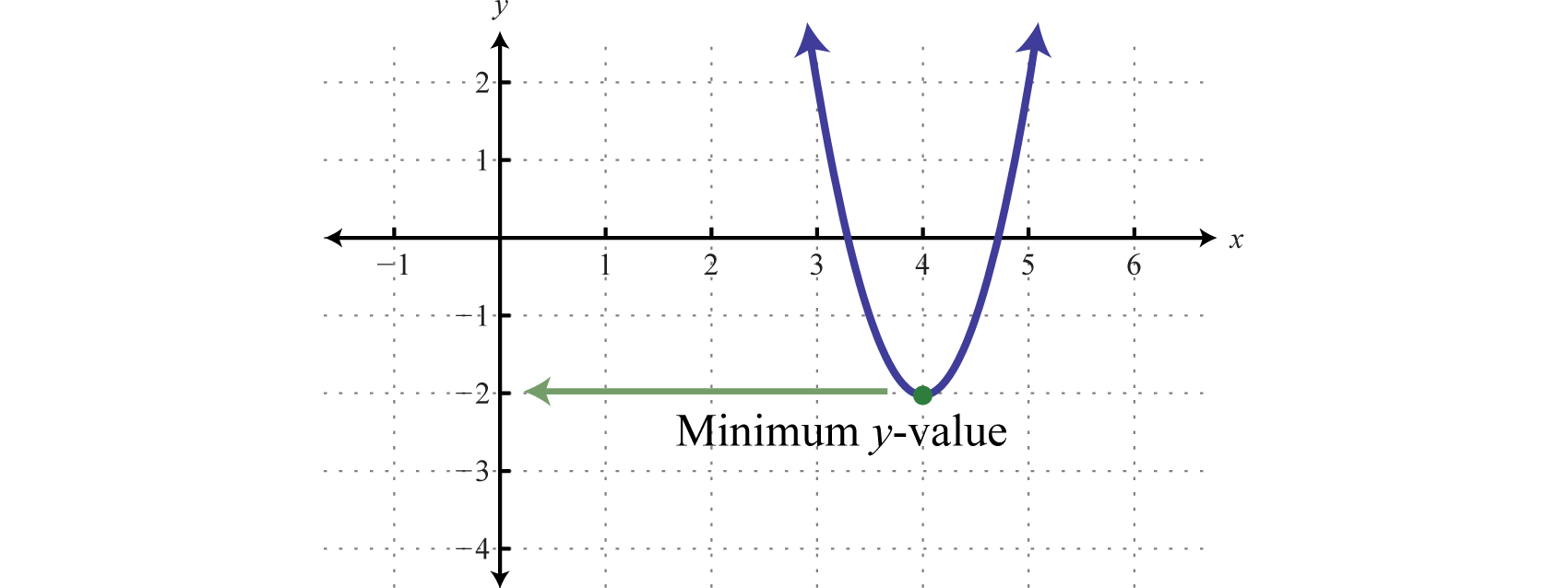
Answer: The minimum is −2.
Example 6
The height in feet of a projectile is given by the function , where t represents the time in seconds after launch. What is the maximum height reached by the projectile?
Solution:
Here , and the parabola opens downward. Therefore, the y-value of the vertex determines the maximum height. Begin by finding the time at which the vertex occurs.
The maximum height will occur in seconds (or seconds). Substitute this time into the function to determine the maximum height attained.
Answer: The maximum height of the projectile is 81 feet.
Finding the Vertex by Completing the Square
In this section, we demonstrate an alternate approach for finding the vertex. Any quadratic function can be rewritten in vertex formA quadratic function written in the form ,
In this form, the vertex is To see that this is the case, consider graphing using the transformations.
Use these translations to sketch the graph,
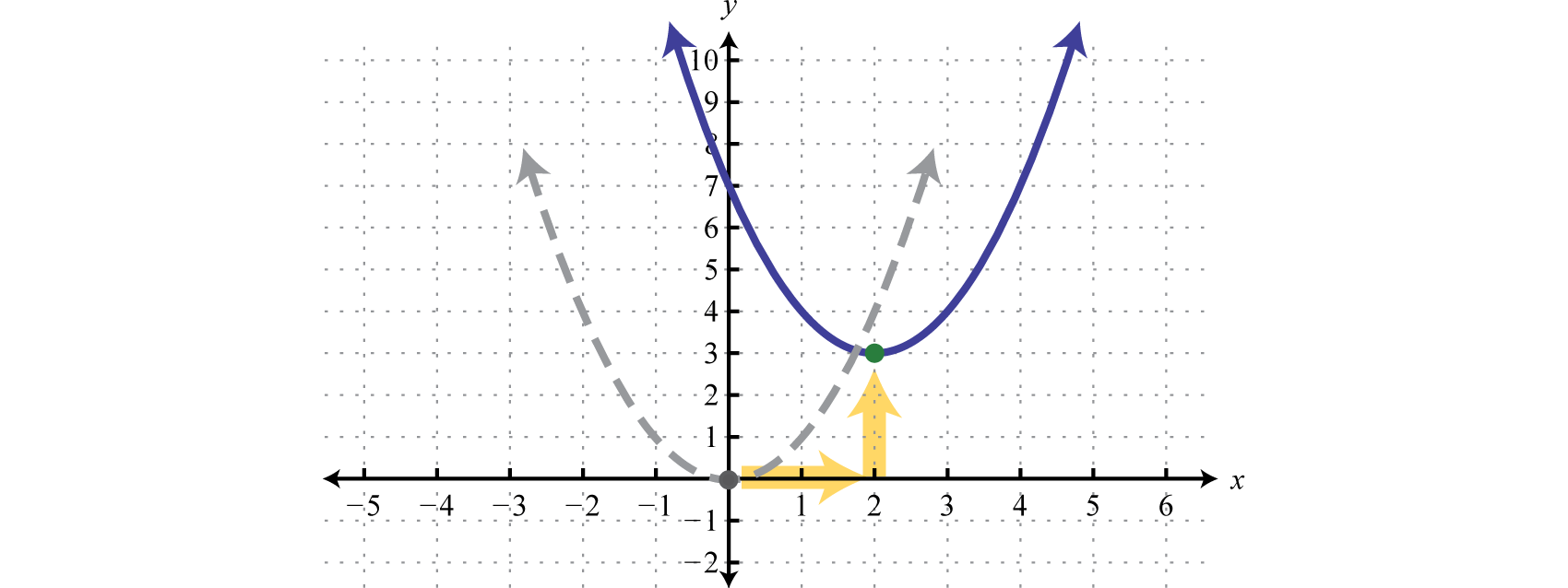
Here we can see that the vertex is (2, 3).
When the equation is in this form, we can read the vertex directly from it.
Example 7
Determine the vertex:
Solution:
Rewrite the equation as follows before determining h and k.
Here h = −3 and k = −2.
Answer: The vertex is (−3, −2).
Often the equation is not given in vertex form. To obtain this form, complete the square.
Example 8
Rewrite in vertex form and determine the vertex:
Solution:
Begin by making room for the constant term that completes the square.
The idea is to add and subtract the value that completes the square, , and then factor. In this case, add and subtract
Adding and subtracting the same value within an expression does not change it. Doing so is equivalent to adding 0. Once the equation is in this form, we can easily determine the vertex.
Here h = −2 and k = 5.
Answer: The vertex is (−2, 5).
If there is a leading coefficient other than 1, then we must first factor out the leading coefficient from the first two terms of the trinomial.
Example 9
Rewrite in vertex form and determine the vertex:
Solution:
Since a = 2, factor this out of the first two terms in order to complete the square. Leave room inside the parentheses to add and subtract the value that completes the square.
Now use −2 to determine the value that completes the square. In this case, Add and subtract 1 and factor as follows:
In this form, we can easily determine the vertex.
Here h = 1 and k = 6.
Answer: The vertex is (1, 6).
Key Takeaways
- The graph of any quadratic function , where a, b, and c are real numbers and , is called a parabola.
- When graphing a parabola always find the vertex and the y-intercept. If the x-intercepts exist, find those as well. Also, be sure to find ordered pair solutions on either side of the line of symmetry,
- Use the leading coefficient, a, to determine if a parabola opens upward or downward. If a is positive, then it opens upward. If a is negative, then it opens downward.
- The vertex of any parabola has an x-value equal to After finding the x-value of the vertex, substitute it into the original equation to find the corresponding y-value. This y-value is a maximum if the parabola opens downward, and it is a minimum if the parabola opens upward.
- The domain of a parabola opening upward or downward consists of all real numbers. The range is bounded by the y-value of the vertex.
- An alternate approach to finding the vertex is to rewrite the quadratic function in the form When in this form, the vertex is and can be read directly from the equation. To obtain this form, take and complete the square.
Topic Exercises
Part A: The Graph of Quadratic Functions
Does the parabola open upward or downward? Explain.
Determine the x- and y-intercepts.
Find the vertex and the line of symmetry.
Graph. Find the vertex and the y-intercept. In addition, find the x-intercepts if they exist.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
The height in feet reached by a baseball tossed upward at a speed of 48 feet per second from the ground is given by the function , where t represents the time in seconds after the ball is thrown. What is the baseball’s maximum height and how long does it take to attain that height?
-
The height in feet of a projectile launched straight up from a mound is given by the function , where t represents seconds after launch. What is the maximum height?
-
The profit in dollars generated by producing and selling x custom lamps is given by the function What is the maximum profit?
-
The profit in dollars generated from producing and selling a particular item is modeled by the formula , where x represents the number of units produced and sold. What number of units must be produced and sold to maximize revenue?
-
The average number of hits to a radio station Web site is modeled by the formula , where t represents the number of hours since 8:00 a.m. At what hour of the day is the number of hits to the Web site at a minimum?
-
The value in dollars of a new car is modeled by the formula , where t represents the number of years since it was purchased. Determine the minimum value of the car.
-
The daily production cost in dollars of a textile manufacturing company producing custom uniforms is modeled by the formula , where x represents the number of uniforms produced.
- How many uniforms should be produced to minimize the daily production costs?
- What is the minimum daily production cost?
-
The area in square feet of a certain rectangular pen is given by the formula , where w represents the width in feet. Determine the width that produces the maximum area.
Part B: Finding the Maximum or Minimum
Determine the maximum or minimum y-value.
Given the following quadratic functions, determine the domain and range.
Part C: Finding the Vertex by Completing the Square
Determine the vertex.
Rewrite in vertex form and determine the vertex.
Graph. Find the vertex and the y-intercept. In addition, find the x-intercepts if they exist.
-
Write down your plan for graphing a parabola on an exam. What will you be looking for and how will you present your answer? Share your plan on the discussion board.
-
Why is any parabola that opens upward or downward a function? Explain to a classmate how to determine the domain and range.
-
Research and discuss ways of finding a quadratic function that has a graph passing through any three given points. Share a list of steps as well as an example of how to do this.
Part D: Discussion Board
Answers
-
Upward
-
-
Downward
-
-
Downward
-
-
x-intercepts: (−6, 0), (2, 0);y-intercept: (0, −12)
-
-
x-intercepts: (−3, 0), ; y-intercept: (0, −3)
-
-
x-intercepts: (−1, 0), ; y-intercept: (0, 2)
-
-
x-intercepts: , ; y-intercept: (0, −27)
-
-
x-intercepts: none; y-intercept: (0, 1)
-
-
Vertex: (5, −9); line of symmetry:
-
-
Vertex: ; line of symmetry:
-
-
Vertex: (0, −1); line of symmetry:
-
-
-
-
-
-
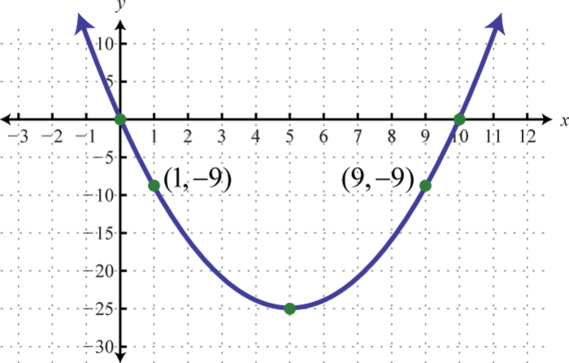
-
-
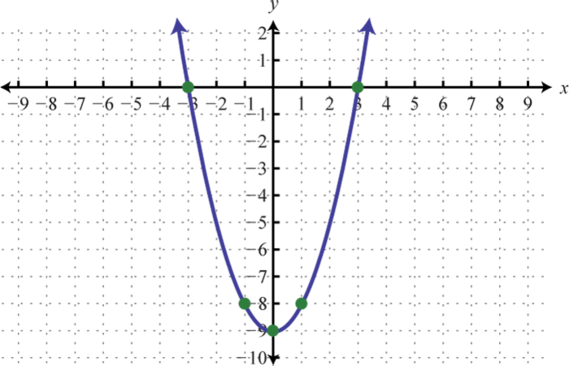
-
-
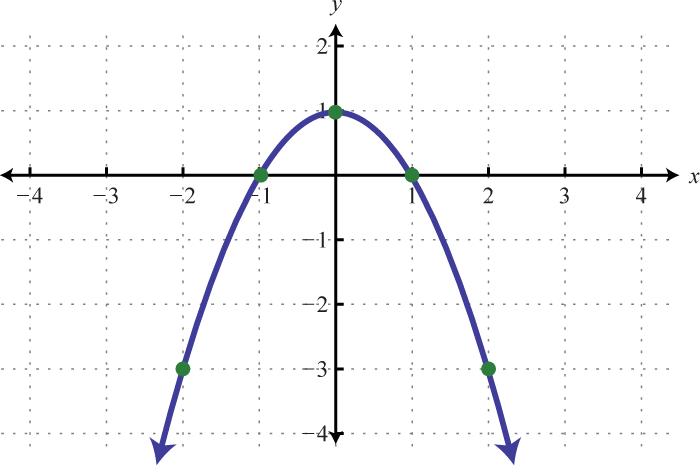
-
-
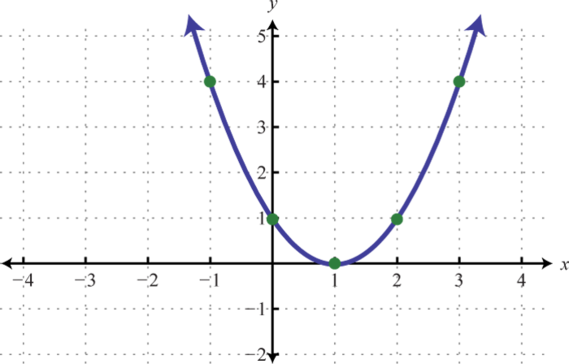
-
-
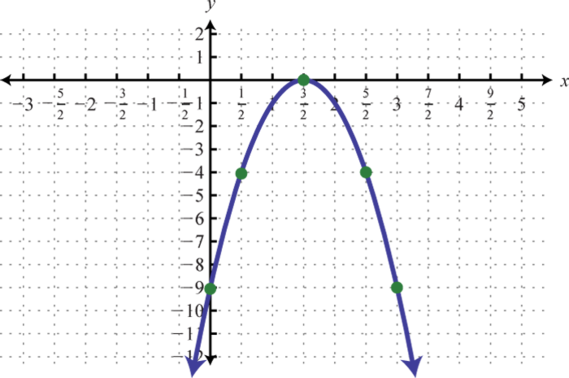
-
-
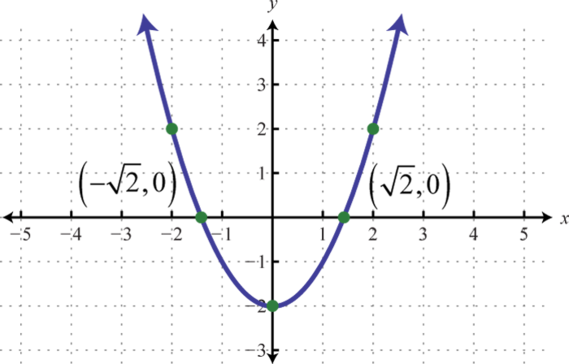
-
-
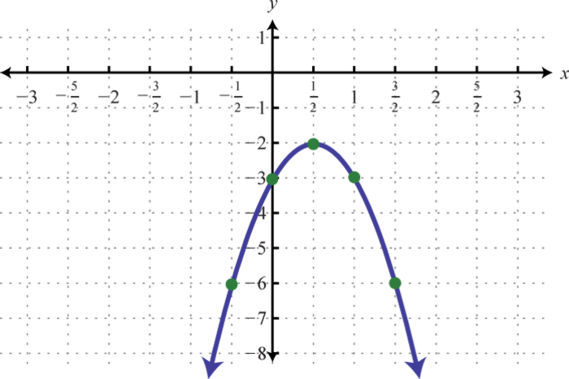
-
-
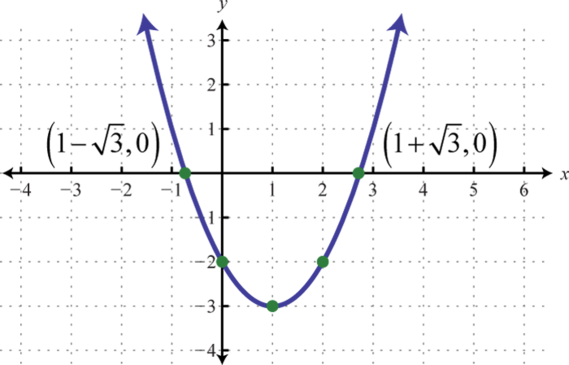
-
-
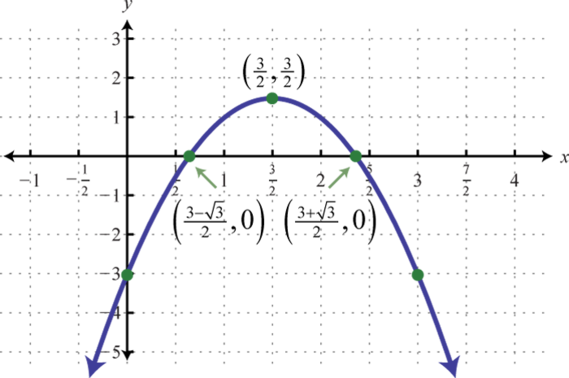
-
-
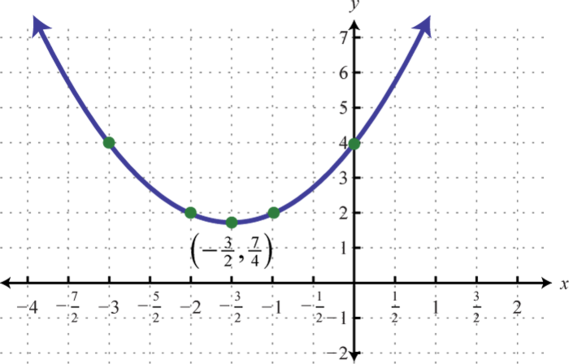
-
-
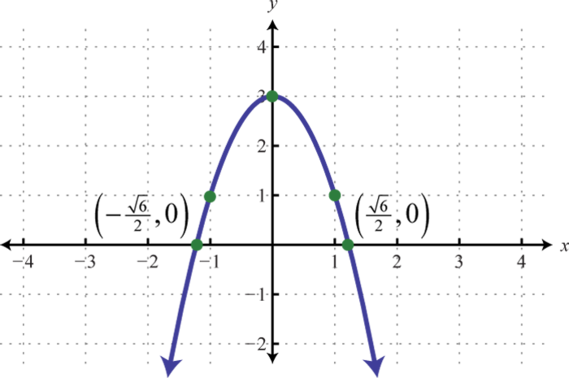
-
-
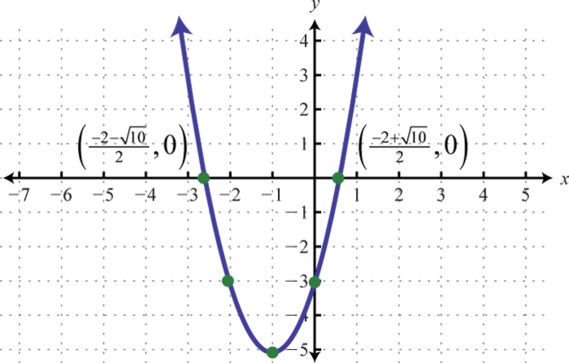
-
-
Maximum: y = 10
-
-
Minimum: y = 4
-
-
Maximum: y = 0
-
-
Maximum: y = 10
-
-
Minimum:
-
-
Minimum:
-
-
Domain: ; range:
-
-
Domain: ; range:
-
-
Domain: ; range:
-
-
The maximum height of 36 feet occurs after 1.5 seconds.
-
-
$4,000
-
-
12:00 p.m.
-
-
- 500 uniforms
- $5,000
-
-
(5, 3)
-
-
(−1, 6)
-
-
(−8, −1)
-
-
; vertex: (7, −25)
-
-
; vertex: (−2, −16)
-
-
; vertex: (3, −21)
-
-
; vertex: (8, 81)
-
-
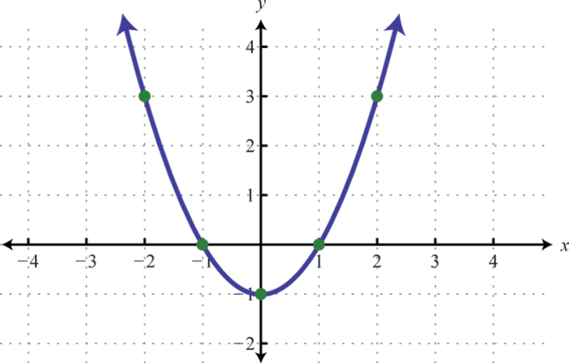
-
-
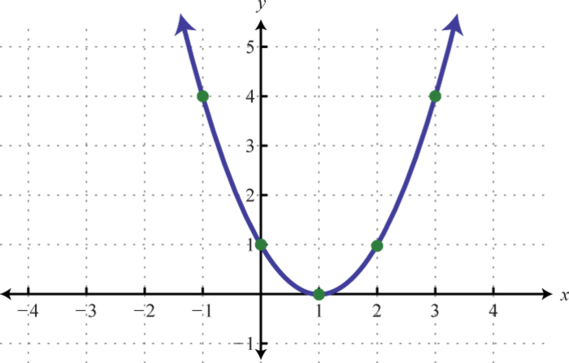
-
-
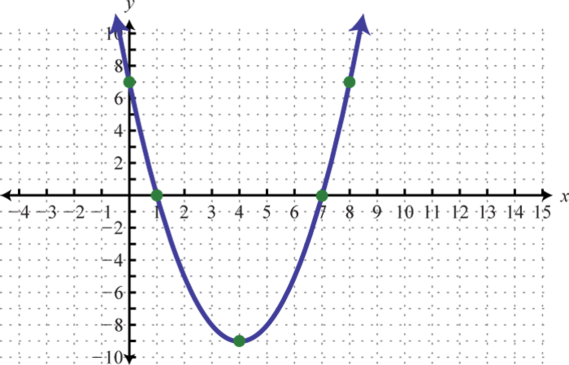
-
-
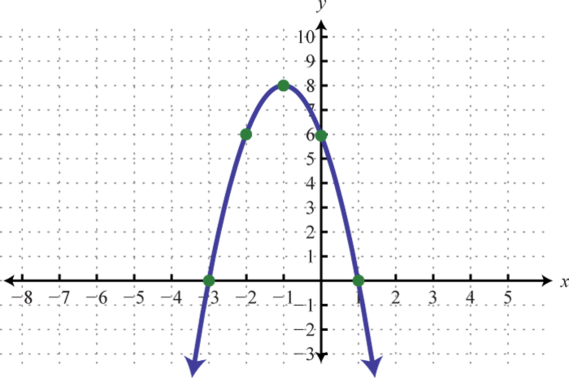
-
-
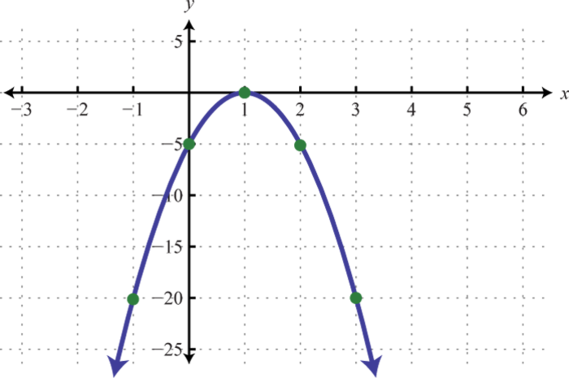
-
-
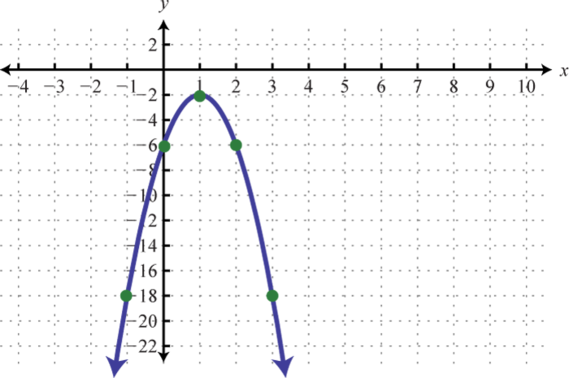
-
-
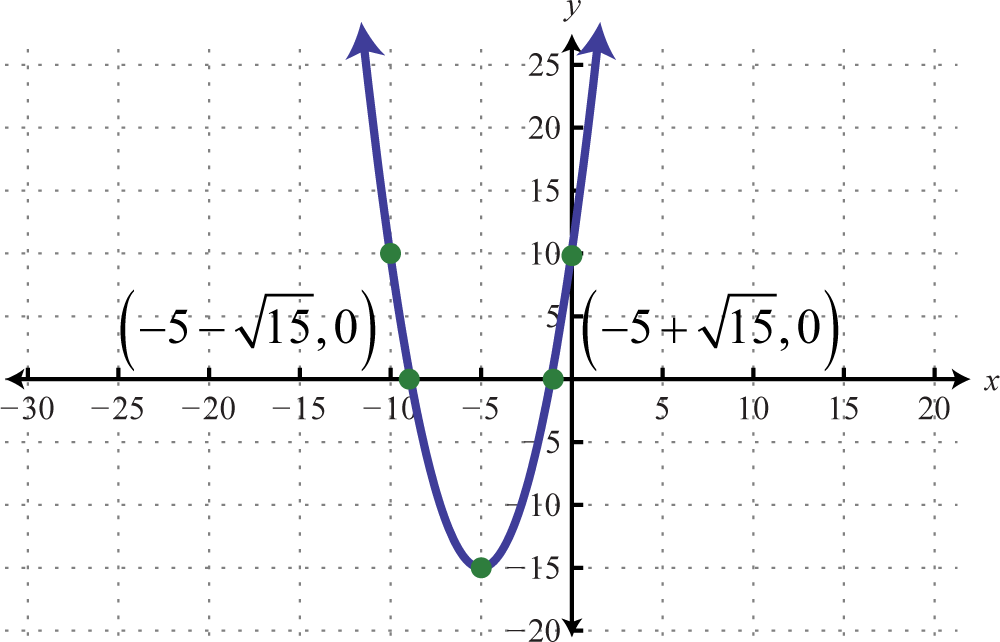
-
-
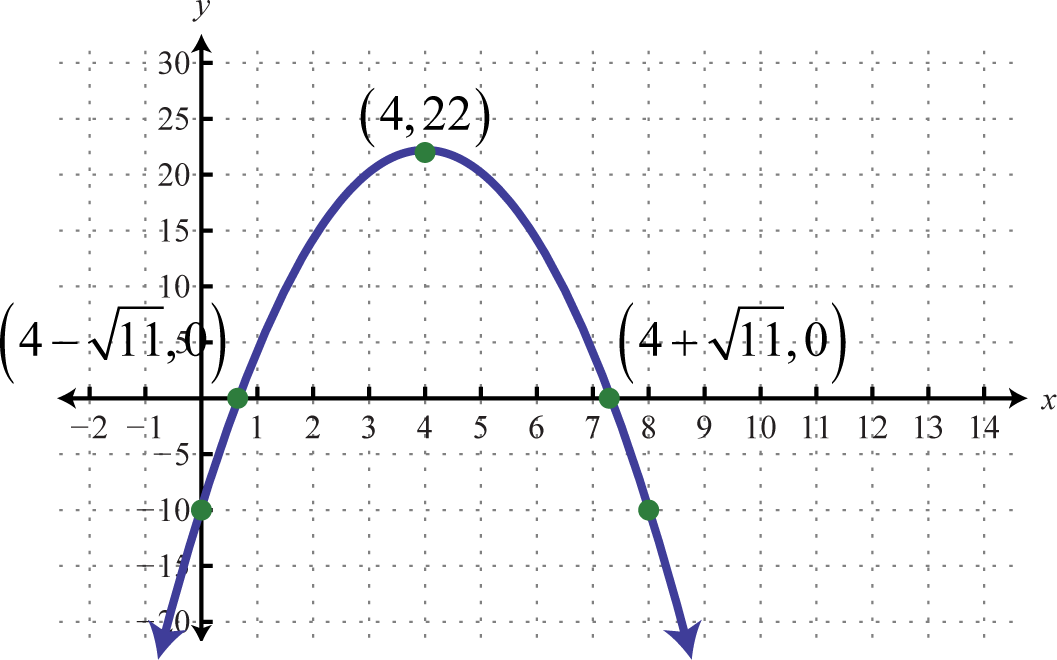
-
-
Answer may vary
-
-
Answer may vary