This is “Solving Radical Equations”, section 5.6 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
5.6 Solving Radical Equations
Learning Objectives
- Solve equations involving square roots.
- Solve equations involving cube roots.
Radical Equations
A radical equationAny equation that contains one or more radicals with a variable in the radicand. is any equation that contains one or more radicals with a variable in the radicand. Following are some examples of radical equations, all of which will be solved in this section:
We begin with the squaring property of equalityGiven real numbers a and b, where , then ; given real numbers a and b, we have the following:
In other words, equality is retained if we square both sides of an equation.
The converse, on the other hand, is not necessarily true,
This is important because we will use this property to solve radical equations. Consider a very simple radical equation that can be solved by inspection,
Here we can see that is a solution. To solve this equation algebraically, make use of the squaring property of equality and the fact that when a is nonnegative. Eliminate the square root by squaring both sides of the equation as follows:
As a check, we can see that as expected. Because the converse of the squaring property of equality is not necessarily true, solutions to the squared equation may not be solutions to the original. Hence squaring both sides of an equation introduces the possibility of extraneous solutionsA properly found solution that does not solve the original equation., which are solutions that do not solve the original equation. For example,
This equation clearly does not have a real number solution. However, squaring both sides gives us a solution:
As a check, we can see that For this reason, we must check the answers that result from squaring both sides of an equation.
Example 1
Solve:
Solution:
We can eliminate the square root by applying the squaring property of equality.
Next, we must check.
Answer: The solution is 5.
There is a geometric interpretation to the previous example. Graph the function defined by and determine where it intersects the graph defined by
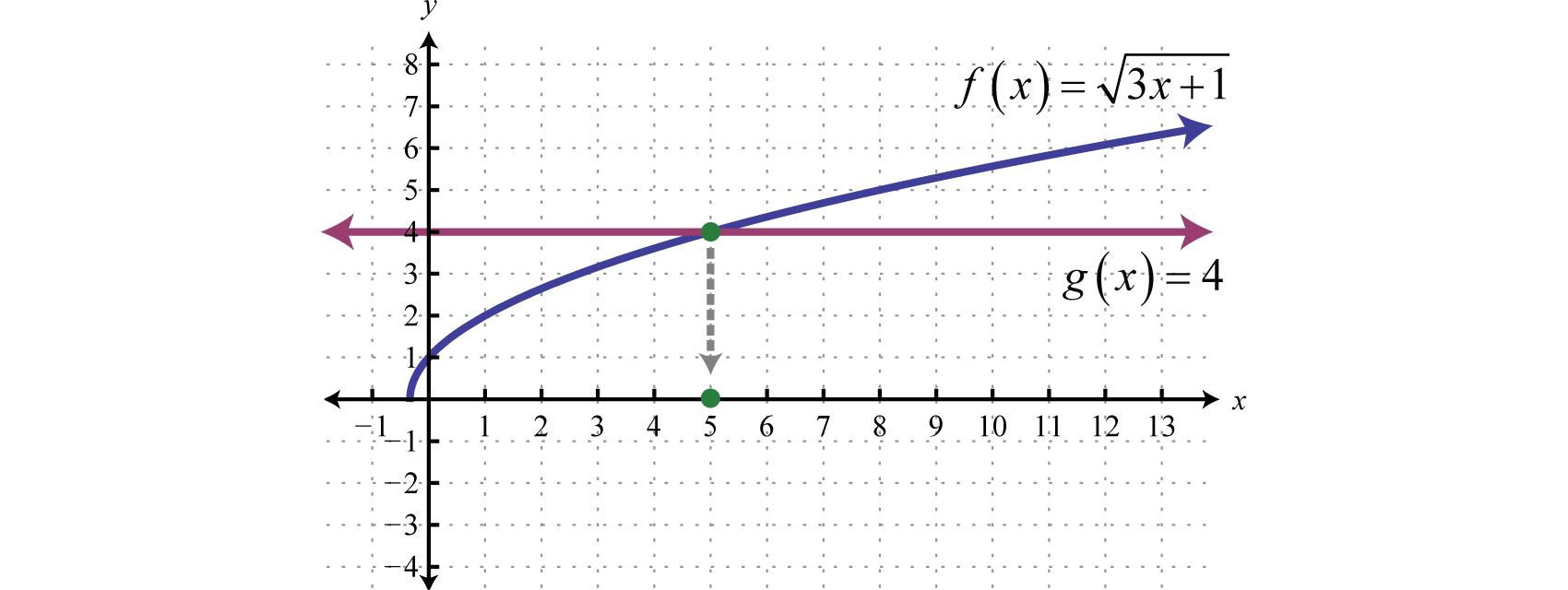
As illustrated, where
Example 2
Solve:
Solution:
Begin by squaring both sides of the equation.
The resulting quadratic equation can be solved by factoring.
Checking the solutions after squaring both sides of an equation is not optional. Use the original equation when performing the check.
After checking, you can see that is an extraneous solution; it does not solve the original radical equation. Disregard that answer. This leaves as the only solution.
Answer: The solution is 7.
Geometrically we can see that is equal to where

In the previous two examples, notice that the radical is isolated on one side of the equation. Typically, this is not the case. The steps for solving radical equations involving square roots are outlined in the following example.
Example 3
Solve:
Solution:
Step 1: Isolate the square root. Begin by subtracting 2 from both sides of the equation.
Step 2: Square both sides. Squaring both sides eliminates the square root.
Step 3: Solve the resulting equation. Here we are left with a quadratic equation that can be solved by factoring.
Step 4: Check the solutions in the original equation. Squaring both sides introduces the possibility of extraneous solutions; hence the check is required.
After checking, we can see that is an extraneous solution; it does not solve the original radical equation. This leaves as the only solution.
Answer: The solution is 5.
Sometimes there is more than one solution to a radical equation.
Example 4
Solve:
Solution:
Begin by isolating the term with the radical.
Despite the fact that the term on the left side has a coefficient, we still consider it to be isolated. Recall that terms are separated by addition or subtraction operators.
Solve the resulting quadratic equation.
Since we squared both sides, we must check our solutions.
After checking, we can see that both are solutions to the original equation.
Answer: The solutions are ±2.
Sometimes both of the possible solutions are extraneous.
Example 5
Solve:
Solution:
Begin by isolating the radical.
Since we squared both sides, we must check our solutions.
Since both possible solutions are extraneous, the equation has no solution.
Answer: No solution, Ø
The squaring property of equality extends to any positive integer power n. Given real numbers a and b, we have the following:
This is often referred to as the power property of equalityGiven any positive integer n and real numbers a and b where , then . Use this property, along with the fact that , when a is nonnegative, to solve radical equations with indices greater than 2.
Example 6
Solve:
Solution:
Isolate the radical, and then cube both sides of the equation.
Check.
Answer: The solutions are .
It may be the case that the equation has more than one term that consists of radical expressions.
Example 7
Solve:
Solution:
Both radicals are considered isolated on separate sides of the equation.
Check
Answer: The solution is 2.
Example 8
Solve:
Solution:
Eliminate the radicals by cubing both sides.
Check.
Answer: The solutions are
It may not be possible to isolate a radical on both sides of the equation. When this is the case, isolate the radicals, one at a time, and apply the squaring property of equality multiple times until only a polynomial remains.
Example 9
Solve:
Solution:
Begin by isolating one of the radicals. In this case, add to both sides of the equation.
Next, square both sides. Take care to apply the distributive property to the right side.
At this point we have one term that contains a radical. Isolate it and square both sides again.
Check to see if satisfies the original equation
Answer: The solution is
Note: Because , we cannot simply square each term. For example, it is incorrect to square each term as follows.
This is a common mistake and leads to an incorrect result. When squaring both sides of an equation with multiple terms, we must take care to apply the distributive property.
Example 10
Solve:
Solution:
Begin by isolating one of the radicals. In this case, add to both sides of the equation.
Next, square both sides. Take care to apply the distributive property to the right side.
At this point we have one term that contains a radical. Isolate it and square both sides again.
Check.
Answer: The solution is 3.
Key Takeaways
- Solve equations involving square roots by first isolating the radical and then squaring both sides. Squaring a square root eliminates the radical, leaving us with an equation that can be solved using the techniques learned earlier in our study of algebra.
- Squaring both sides of an equation introduces the possibility of extraneous solutions. For this reason, you must check your solutions in the original equation.
- Solve equations involving nth roots by first isolating the radical and then raise both sides to the nth power. This eliminates the radical and results in an equation that may be solved with techniques you have already mastered.
- When more than one radical term is present in an equation, isolate them one at a time, and apply the power property of equality multiple times until only a polynomial remains.
Topic Exercises
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Solve for P:
-
Solve for x:
-
Solve for s:
-
Solve for L:
-
Solve for R:
-
Solve for h:
-
Solve for V:
-
Solve for c:
-
The square root of 1 less than twice a number is equal to 2 less than the number. Find the number.
-
The square root of 4 less than twice a number is equal to 6 less than the number. Find the number.
-
The square root of twice a number is equal to one-half of that number. Find the number.
-
The square root of twice a number is equal to one-third of that number. Find the number.
-
The distance d in miles a person can see an object on the horizon is given by the formula where h represents the height in feet of the person’s eyes above sea level. How high must a person’s eyes be to see an object 5 miles away?
-
The current I measured in amperes is given by the formula where P is the power usage measured in watts and R is the resistance measured in ohms. If a light bulb requires 1/2 amperes of current and uses 60 watts of power, then what is the resistance through the bulb?
-
1 second
-
2 seconds
-
second
-
second
-
1 second
-
2 seconds
-
second
-
second
Part A: Solving Radical Equations
Solve
Determine the roots of the given functions. Recall that a root is a value in the domain that results in zero. In other words, find where
Solve for the indicated variable.
The period of a pendulum T in seconds is given by the formula where L represents the length in feet. Calculate the length of a pendulum given the period. Give the exact value and the approximate value rounded to the nearest tenth of a foot.
The time t in seconds, an object is in free fall is given by the formula where s represents the distance it has fallen, in feet. Calculate the distance an object will fall given the amount of time.
-
Discuss reasons why we sometimes obtain extraneous solutions when solving radical equations. Are there ever any conditions where we do not need to check for extraneous solutions? Why or why not?
-
If an equation has multiple terms, explain why squaring all of them is incorrect. Provide an example.
Part B: Discussion Board
Answers
-
49
-
-
1
-
-
Ø
-
-
-
-
1
-
-
3
-
-
-
-
0
-
-
-
-
Ø
-
-
27
-
-
9
-
-
−3
-
-
6
-
-
-
-
2
-
-
7
-
-
2
-
-
−3
-
-
13
-
-
7
-
-
2, 6
-
-
2
-
-
−1, 8
-
-
5
-
-
Ø
-
-
−3, 3
-
-
2, 5
-
-
−4, 4
-
-
-
-
2, 7
-
-
Ø
-
-
10
-
-
−6, −4
-
-
-
-
Ø
-
-
−5, 5
-
-
−9, 3
-
-
-
-
-
-
−1, 1/2
-
-
5, 10
-
-
−7, 7
-
-
-
-
1
-
-
10
-
-
Ø
-
-
3
-
-
−1, 2
-
-
100
-
-
−8
-
-
10
-
-
−13
-
-
-
-
−6, −4
-
-
−2, 2
-
-
1
-
-
−2
-
-
−1
-
-
14
-
-
−9
-
-
-
-
-
-
-
-
-
-
5
-
-
0, 8
-
-
feet
-
-
feet; 0.8 feet
-
-
feet; 0.2 feet
-
-
16 feet
-
-
4 feet
-
-
Answer may vary
-




