This is “Factoring Trinomials”, section 4.3 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
4.3 Factoring Trinomials
Learning Objectives
- Factor trinomials of the form
- Factor trinomials of higher degree.
- Factor trinomials of the form
- Factor trinomials using the AC method.
Factoring Trinomials of the Form
Some trinomials of the form can be factored as a product of binomials. If a trinomial of this type factors, then we have:
This gives us
In short, if the leading coefficient of a factorable trinomial is 1, then the factors of the last term must add up to the coefficient of the middle term. This observation is the key to factoring trinomials using the technique known as the trial and error (or guess and check) methodDescribes the method of factoring a trinomial by systematically checking factors to see if their product is the original trinomial..
Example 1
Factor:
Solution:
We begin by writing two sets of blank parentheses. If a trinomial of this form factors, then it will factor into two linear binomial factors.
Write the factors of the first term in the first space of each set of parentheses. In this case, factor
Determine the factors of the last term whose sum equals the coefficient of the middle term. To do this, list all of the factorizations of 20 and search for factors whose sum equals 12.
Choose 20 = 2 ⋅ 10 because 2 + 10 = 12. Write in the last term of each binomial using the factors determined in the previous step.
This can be visually interpreted as follows:
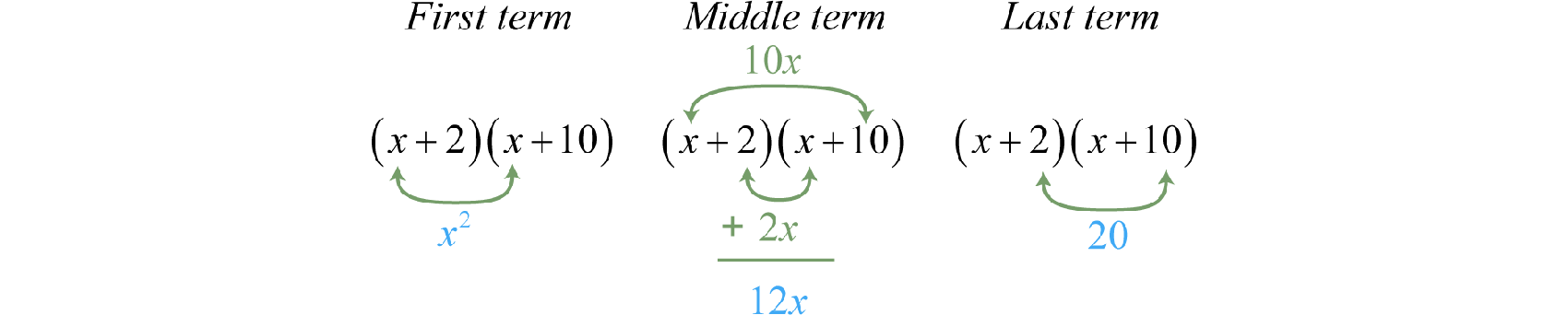
Check by multiplying the two binomials.
Answer:
Since multiplication is commutative, the order of the factors does not matter.
If the last term of the trinomial is positive, then either both of the constant factors must be negative or both must be positive.
Example 2
Factor:
Solution:
First, factor
Next, search for factors of 12 whose sum is −7.
In this case, choose −3 and −4 because and
Check.
Answer:
If the last term of the trinomial is negative, then one of its factors must be negative.
Example 3
Factor:
Solution:
Begin by factoring the first term
The factors of 12 are listed below. In this example, we are looking for factors whose sum is −4.
Therefore, the coefficient of the last term can be factored as , where Because the last term has a variable factor of , use and factor the trinomial as follows:
Multiply to check.
Answer:
Often our first guess will not produce a correct factorization. This process may require repeated trials. For this reason, the check is very important and is not optional.
Example 4
Factor:
Solution:
The first term of this trinomial, , factors as
Consider the factors of 24:
Suppose we choose the factors 4 and 6 because 4 + 6 = 10, the coefficient of the middle term. Then we have the following incorrect factorization:
When we multiply to check, we find the error.
In this case, the middle term is correct but the last term is not. Since the last term in the original expression is negative, we need to choose factors that are opposite in sign. Therefore, we must try again. This time we choose the factors −2 and 12 because
Now the check shows that this factorization is correct.
Answer:
If we choose the factors wisely, then we can reduce much of the guesswork in this process. However, if a guess is not correct, do not get discouraged; just try a different set of factors. Keep in mind that some polynomials are prime. For example, consider the trinomial and the factors of 20:
There are no factors of 20 whose sum is 3. Therefore, the original trinomial cannot be factored as a product of two binomials with integer coefficients. The trinomial is prime.
Factoring Trinomials of Higher Degree
We can use the trial and error technique to factor trinomials of higher degree.
Example 5
Factor:
Solution:
Begin by factoring the first term
Since 5 is prime and the coefficient of the middle term is positive, choose +1 and +5 as the factors of the last term.
Notice that the variable part of the middle term is and the factorization checks out.
Answer:
Example 6
Factor: where n is a positive integer.
Solution:
Begin by factoring the first term
Factor because and write
Answer: The check is left to the reader.
Factoring Trinomials of the Form
Factoring trinomials of the form can be challenging because the middle term is affected by the factors of both and In general,
This gives us,
In short, when the leading coefficient of a trinomial is something other than 1, there will be more to consider when determining the factors using the trial and error method. The key lies in the understanding of how the middle term is obtained. Multiply and carefully follow the formation of the middle term.

As we have seen before, the product of the first terms of each binomial is equal to the first term of the trinomial. The middle term of the trinomial is the sum of the products of the outer and inner terms of the binomials. The product of the last terms of each binomial is equal to the last term of the trinomial. Visually, we have the following:

For this reason, we need to look for products of the factors of the first and last terms whose sum is equal to the coefficient of the middle term. For example, to factor , look at the factors of 6 and 35.
The combination that produces the coefficient of the middle term is Make sure that the outer terms have coefficients 2 and 7, and that the inner terms have coefficients 5 and 3. Use this information to factor the trinomial.
We can always check by multiplying; this is left to the reader.
Example 7
Factor:
Solution:
Since the leading coefficient and the last term are both prime, there is only one way to factor each.
Begin by writing the factors of the first term, , as follows:
The middle and last term are both positive; therefore, the factors of 3 are chosen as positive numbers. In this case, the only choice is in which grouping to place these factors.
Determine which grouping is correct by multiplying each expression.
Answer:
Example 8
Factor:
Solution:
First, consider the factors of the coefficients of the first and last terms.
We are searching for products of factors whose sum equals the coefficient of the middle term, −1. After some thought, we can see that the sum of 8 and −9 is −1 and the combination that gives this follows:
Factoring begins at this point with two sets of blank parentheses.
Use and as factors of
Next use the factors 1 and 4 in the correct order so that the inner and outer products are and respectively.
Answer: The complete check is left to the reader.
It is a good practice to first factor out the GCF, if there is one. Doing this produces a trinomial factor with smaller coefficients. As we have seen, trinomials with smaller coefficients require much less effort to factor. This commonly overlooked step is worth identifying early.
Example 9
Factor:
Solution:
Begin by factoring out the GCF.
After factoring out , the coefficients of the resulting trinomial are smaller and have fewer factors. We can factor the resulting trinomial using and Notice that these factors can produce −13 in two ways:
Because the last term is −5, the correct combination requires the factors 1 and 5 to be opposite signs. Here we use 2(1) = 2 and 3(−5) = −15 because the sum is −13 and the product of (1)(−5) = −5.
Check.
The factor is part of the factored form of the original expression; be sure to include it in the answer.
Answer:
It is a good practice to consistently work with trinomials where the leading coefficient is positive. If the leading coefficient is negative, factor it out along with any GCF. Note that sometimes the factor will be −1.
Example 10
Factor:
Solution:
In this example, the GCF is Because the leading coefficient is negative we begin by factoring out
At this point, factor the remaining trinomial as usual, remembering to write the as a factor in the final answer. Use 6 = 1(6) and −4 = 4(−1) because Therefore,
Answer: The check is left to the reader.
Factoring Using the AC Method
An alternate technique for factoring trinomials, called the AC methodMethod used for factoring trinomials by replacing the middle term with two terms that allow us to factor the resulting four-term polynomial by grouping., makes use of the grouping method for factoring four-term polynomials. If a trinomial in the form can be factored, then the middle term, bx, can be replaced with two terms with coefficients whose sum is b and product is ac. This substitution results in an equivalent expression with four terms that can be factored by grouping.
Example 11
Factor using the AC method:
Solution:
Here a = 18, b = −31, and c = 6.
Factor 108, and search for factors whose sum is −31.
In this case, the sum of the factors −27 and −4 equals the middle coefficient, −31. Therefore, , and we can write
Factor the equivalent expression by grouping.
Answer:
Example 12
Factor using the AC method:
Solution:
Here a = 4, b = −7, and c = −15.
Factor −60 and search for factors whose sum is −7.
The sum of factors 5 and −12 equals the middle coefficient, −7. Replace with
Answer: The check is left to the reader.
If factors of ac cannot be found to add up to b then the trinomial is prime.
Key Takeaways
- If a trinomial of the form factors into the product of two binomials, then the coefficient of the middle term is the sum of factors of the last term.
- If a trinomial of the form factors into the product of two binomials, then the coefficient of the middle term will be the sum of certain products of factors of the first and last terms.
- If the trinomial has a greatest common factor, then it is a best practice to first factor out the GCF before attempting to factor it into a product of binomials.
- If the leading coefficient of a trinomial is negative, then it is a best practice to first factor that negative factor out before attempting to factor the trinomial.
- Factoring is one of the more important skills required in algebra. For this reason, you should practice working as many problems as it takes to become proficient.
Topic Exercises
Part A: Factoring Trinomials of the Form
Factor.
Part B: Factoring Trinomials of the Form
Factor.
Factor.
-
Create your own trinomial of the form that factors. Share it, along with the solution, on the discussion board.
-
Create a trinomial of the form that does not factor and share it along with the reason why it does not factor.
Part D: Discussion Board
Answers
-
-
-
-
-
-
-
Prime
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Prime
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Prime
-
-
-
-
Answer may vary
-




