This is “Review Exercises and Sample Exam”, section 3.8 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
3.8 Review Exercises and Sample Exam
Review Exercises
-
;
-
;
-
;
-
;
-
-
-
-
-
-
-
-
-
-
-
-
Linear Systems and Their Solutions
Determine whether or not the given ordered pair is a solution to the given system.
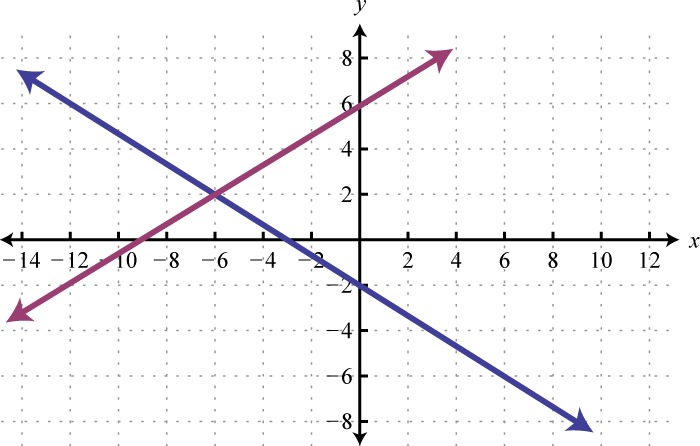
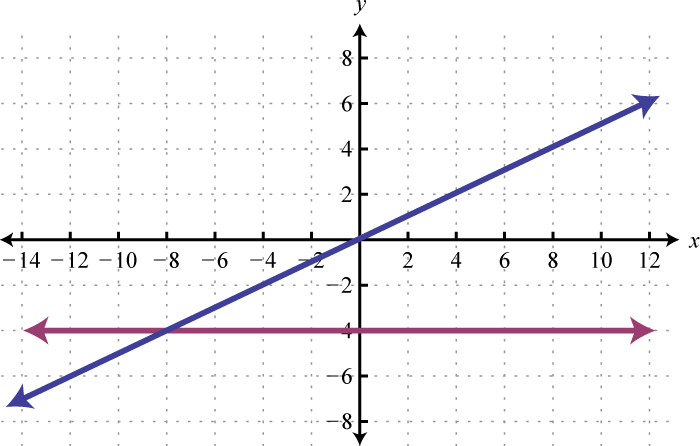
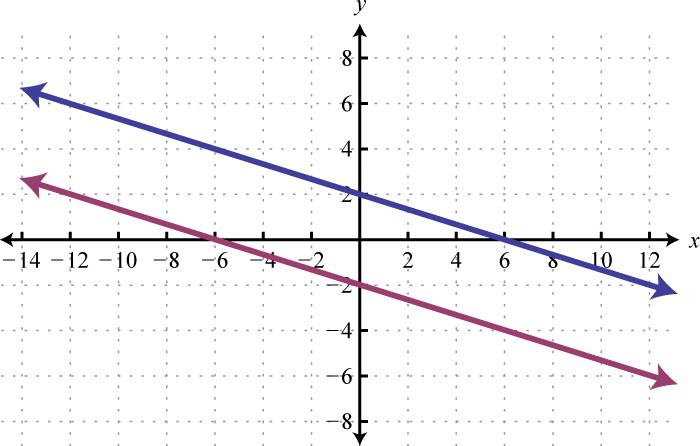
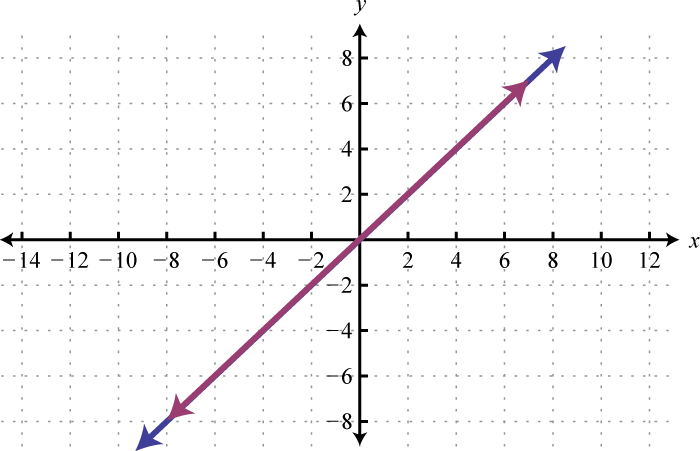
Given the graphs, determine the simultaneous solution.
Solve by graphing.
Solving Linear Systems with Two Variables
Solve by substitution.
Solve by elimination.
Solve using any method.
-
The sum of two integers is 32. The larger is 4 less than twice the smaller. Find the integers.
-
The sum of 2 times a larger integer and 3 times a smaller integer is 54. When twice the smaller integer is subtracted from the larger, the result is −1. Find the integers.
-
The length of a rectangle is 2 centimeters less than three times its width and the perimeter measures 44 centimeters. Find the dimensions of the rectangle.
-
The width of a rectangle is one-third of its length. If the perimeter measures centimeters, then find the dimensions of the rectangle.
-
The sum of a larger integer and 3 times a smaller is 61. When twice the smaller integer is subtracted from the larger, the result is 1. Find the integers.
-
A total of $8,600 was invested in two accounts. One account earned % annual interest and the other earned % annual interest. If the total interest for one year was $431.25, how much was invested in each account?
-
A jar consisting of only nickels and dimes contains 76 coins. If the total value is $6, how many of each coin are in the jar?
-
A nurse wishes to obtain 32 ounces of a 1.2% saline solution. How much of a 1% saline solution must she mix with a 2.6% saline solution to achieve the desired mixture?
-
A light aircraft flying with the wind can travel 330 miles in 2 hours. The aircraft can fly the same distance against the wind in 3 hours. Find the speed of the wind.
-
An executive was able to average 52 miles per hour to the airport in her car and then board an airplane that averaged 340 miles per hour. If the total 640-mile business trip took 4 hours, how long did she spend on the airplane?
Applications of Linear Systems with Two Variables
Set up a linear system and solve.
-
;
-
;
-
;
-
;
-
-
-
-
-
-
-
-
-
The sum of three integers is 24. The larger is equal to the sum of the two smaller integers. Three times the smaller is equal to the larger. Find the integers.
-
The sports center sold 120 tickets to the Friday night basketball game for a total of $942. A general admission ticket cost $12, a student ticket cost $6, and a child ticket cost $4. If the sum of the general admission and student tickets totaled 105, then how many of each ticket were sold?
-
A 16-ounce mixed nut product containing 13.5% peanuts is to be packaged. The packager has a three-mixed nut product containing 6%, 10%, and 50% peanut concentrations in stock. If the amount of 50% peanut product is to be one-quarter that of the 10% peanut product, then how much of each will be needed to produce the desired peanut concentration?
-
Water is to be mixed with two acid solutions to produce a 25-ounce solution containing 6% acid. The acid mixtures on hand contain 10% and 25% acid. If the amount of 25% acid is to be one-half the amount of the 10% acid solution, how much water will be needed?
Solving Linear Systems with Three Variables
Determine whether the given ordered triple is a solution to the given system.
Solve.
Set up a linear system and solve.
Matrices and Gaussian Elimination
Construct the corresponding augmented matrix.
Solve using matrices and Gaussian elimination.
Determinants and Cramer’s Rule
Calculate the determinant.
Solve using Cramer’s rule.
-
(−6, 1);
-
;
-
(−4, −2);
-
;
-
(−3, −2);
-
;
-
-
-
-
-
-
-
-
Systems of Inequalities with Two Variables
Determine whether or not the given point is a solution to the system of inequalities.
Graph the solution set.
Answers
-
Yes
-
-
No
-
-
(−6, 2)
-
-
Ø
-
-
(4, −2)
-
-
-
-
(4, 5)
-
-
(6, 0)
-
-
(2, −4)
-
-
-
-
-
-
(4, 3)
-
-
(5, 2)
-
-
-
-
Ø
-
-
-
-
12, 20
-
-
Length: 16 centimeters; width: 6 centimeters
-
-
12, 25
-
-
The jar contains 32 nickels and 44 dimes.
-
-
27.5 miles per hour
-
-
No
-
-
Yes
-
-
-
-
(−2, −1, 3)
-
-
Ø
-
-
-
-
4, 8, 12
-
-
6 oz of the 6% peanut stock, 8 oz of the 10% peanut stock, and 2 oz of the 50% peanut stock should be mixed.
-
-
-
-
-
-
(5, −4)
-
-
-
-
-
-
(−2, 2, 2)
-
-
−22
-
-
−14
-
-
−1
-
-
0
-
-
-
-
-
-
(2, −5, 1)
-
-
-
-
-
-
Yes
-
-
Yes
-
-
Yes
-
-
-
-
-
-
-
-
-
Sample Exam
-
Determine whether or not is a solution to .
-
Determine whether or not is a solution to .
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
The length of a rectangle is 1 inch less than twice that of its width. If the perimeter measures 49 inches, then find the dimensions of the rectangle.
-
Joe’s $4,000 savings is in two accounts. One account earns 3.1% annual interest and the other earns 4.9% annual interest. His total interest for the year is $174.40. How much does he have in each account?
-
One solution contains 40% alcohol and another contains 72% alcohol. How much of each should be mixed together to obtain 16 ounces of a 62% alcohol solution?
-
Jerry took two buses on the 193-mile trip to visit his grandmother. The first bus averaged 46 miles per hour and the second bus was able to average 52 miles per hour. If the total trip took 4 hours, then how long was spent in each bus?
-
A total of $8,500 was invested in three interest earning accounts. The interest rates were 2%, 3%, and 6%. If the total simple interest for one year was $380 and the amount invested at 6% was equal to the sum of the amounts in the other two accounts, then how much was invested in each account?
-
A mechanic wishes to mix 6 gallons of a 22% antifreeze solution. In stock he has a 60% and an 80% antifreeze concentrate. Water is to be added in the amount that is equal to twice the amount of both concentrates combined. How much water is needed?
Solve by graphing.
Solve by substitution.
Solve.
Solve using any method.
Graph the solution set.
Use algebra to solve the following.
Answers
-
Yes
-
-
(−4, 1)
-
-
-
-
(−8, −3)
-
-
(4, −3)
-
-
Ø
-
-
-
-
Ø
-
-
(2, 2, 2)
-
-
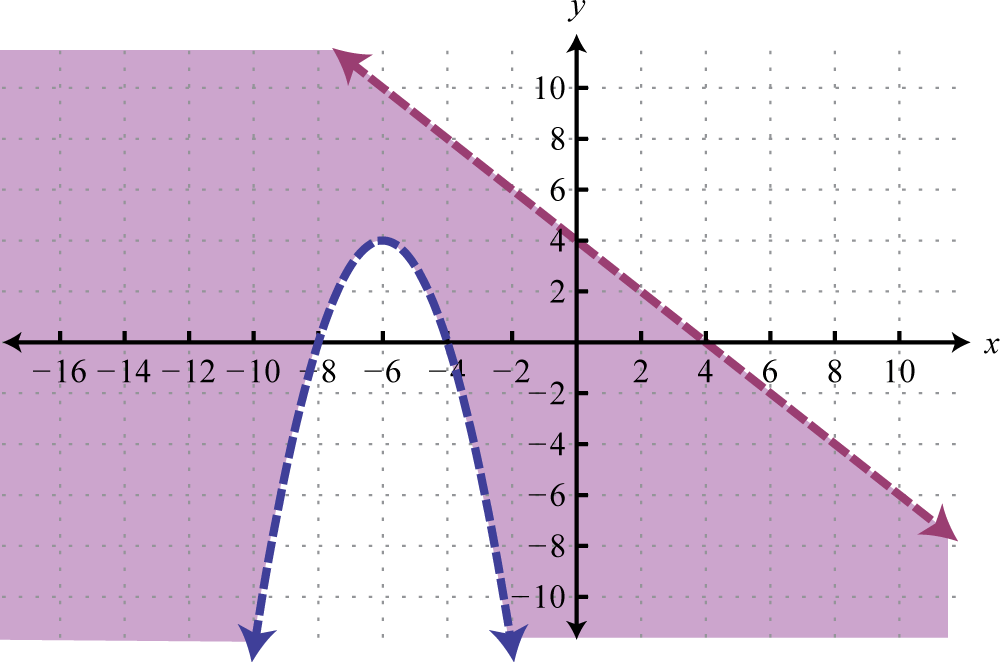
-
-
Joe has $1,200 in the account earning 3.1% interest and $2,800 in the account earning 4.9% interest.
-
-
Jerry spent 2.5 hours in the first bus and 1.5 hours in the second.
-
-
4 gallons of water is needed.




