This is “Solving Linear Systems with Two Variables”, section 3.2 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
3.2 Solving Linear Systems with Two Variables
Learning Objectives
- Solve linear systems using the substitution method.
- Solve linear systems using the elimination method.
- Identify the strengths and weaknesses of each method.
The Substitution Method
In this section, we review a completely algebraic technique for solving systems, the substitution methodA means of solving a linear system by solving for one of the variables and substituting the result into the other equation.. The idea is to solve one equation for one of the variables and substitute the result into the other equation. After performing this substitution step, we are left with a single equation with one variable, which can be solved using algebra.
Example 1
Solve by substitution: .
Solution:
Solve for either variable in either equation. If you choose the first equation, you can isolate y in one step.
Substitute the expression for the variable y in the other equation.

This leaves us with an equivalent equation with one variable, which can be solved using the techniques learned up to this point. Solve for the remaining variable.
Back substituteOnce a value is found for a variable, substitute it back into one of the original equations, or its equivalent, to determine the corresponding value of the other variable. to find the other coordinate. Substitute x = −2 into either of the original equations or their equivalents. Typically, we use the equivalent equation that we found when isolating a variable in the first step.
Remember to present the solution as an ordered pair: . Verify that these coordinates solve both equations of the original system:
Check: (−2, 1) |
|
|---|---|
Equation 1 |
Equation 2 |
The graph of this linear system follows:
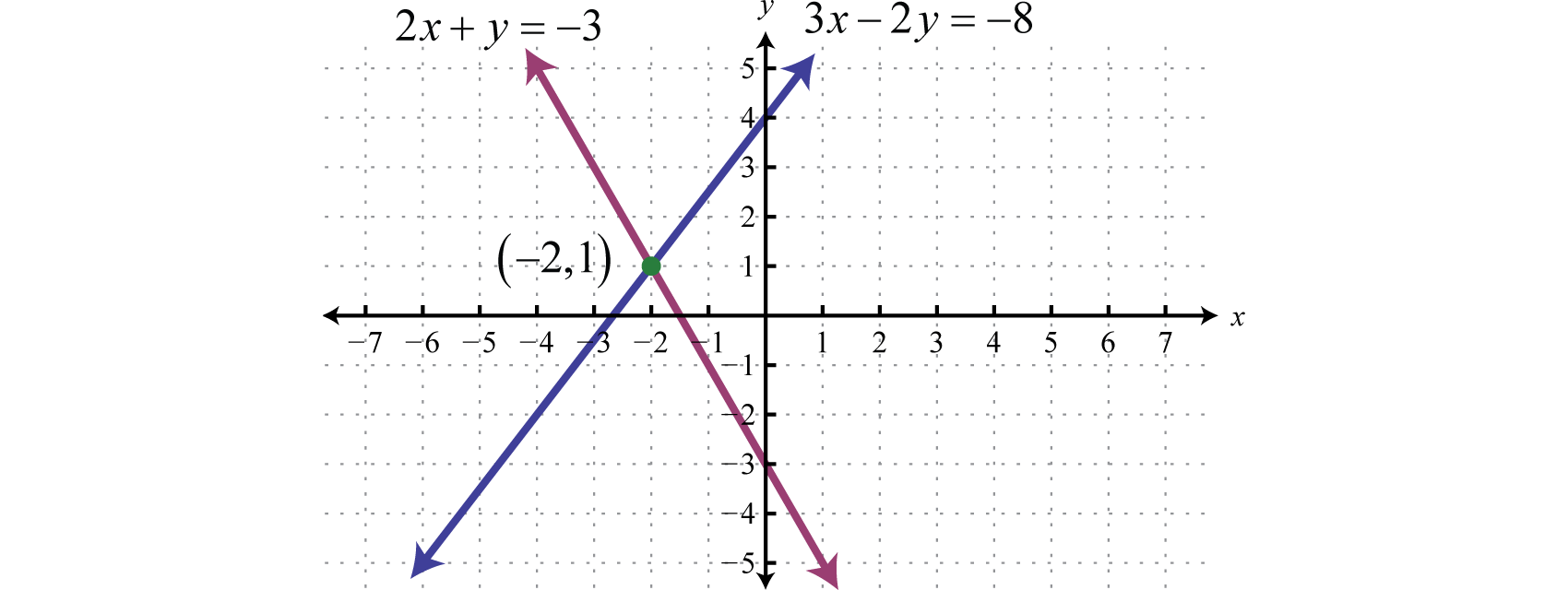
The substitution method for solving systems is a completely algebraic method. Thus graphing the lines is not required.
Answer: (−2, 1)
Example 2
Solve by substitution: .
Solution:
It does not matter which variable we choose to isolate first. In this case, begin by solving for x in the first equation.
Next, substitute into the second equation and solve for y.
Back substitute into the equation used in the substitution step:
Answer:
As we know, not all linear systems have only one ordered pair solution. Next, we explore what happens when using the substitution method to solve a dependent system.
Example 3
Solve by substitution: .
Solution:
Since the first equation has a term with coefficient 1, we choose to solve for that first.
Next, substitute this expression in for y in the second equation.
This process led to a true statement; hence the equation is an identity and any real number is a solution. This indicates that the system is dependent. The simultaneous solutions take the form , or in this case, , where x is any real number.
Answer:
To have a better understanding of the previous example, rewrite both equations in slope-intercept form and graph them on the same set of axes.
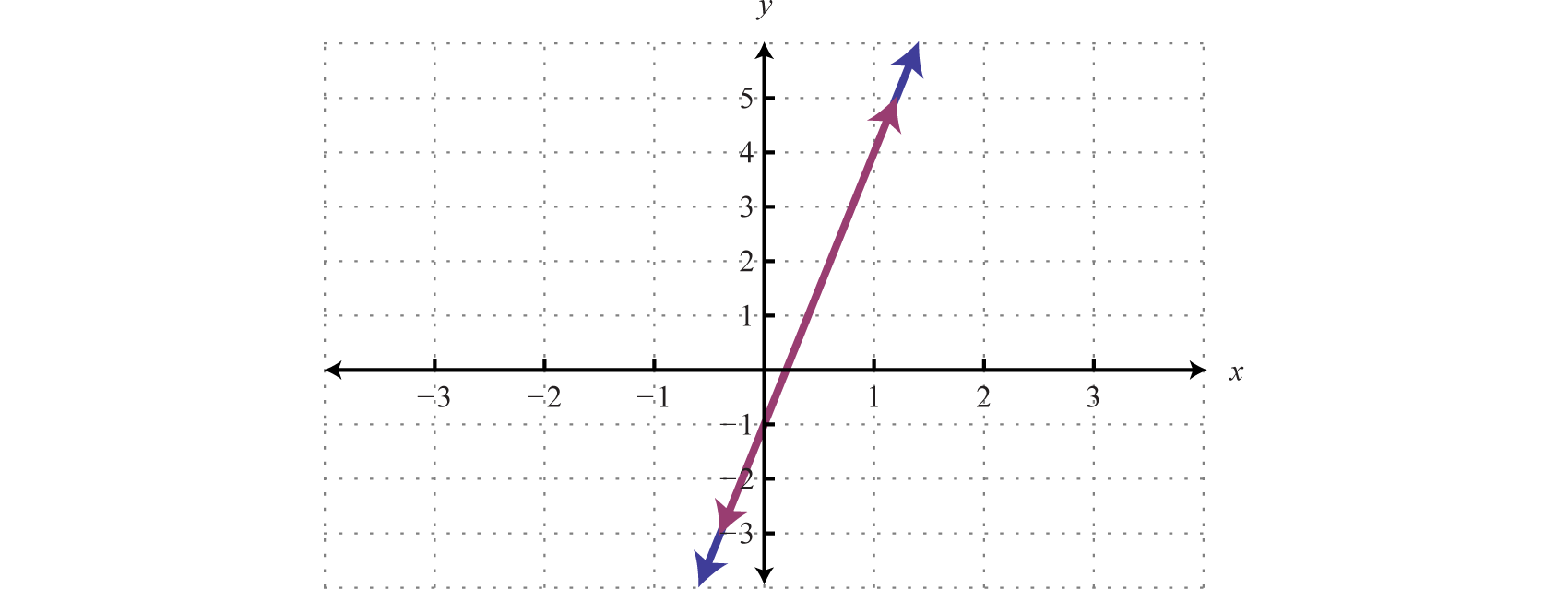
We can see that both equations represent the same line, and thus the system is dependent. Now explore what happens when solving an inconsistent system using the substitution method.
Example 4
Solve by substitution: .
Solution:
Solve for y in the first equation.
Substitute into the second equation and solve.
Solving leads to a false statement. This indicates that the equation is a contradiction. There is no solution for x and hence no solution to the system.
Answer: Ø
A false statement indicates that the system is inconsistent, or in geometric terms, that the lines are parallel and do not intersect. To illustrate this, determine the slope-intercept form of each line and graph them on the same set of axes.
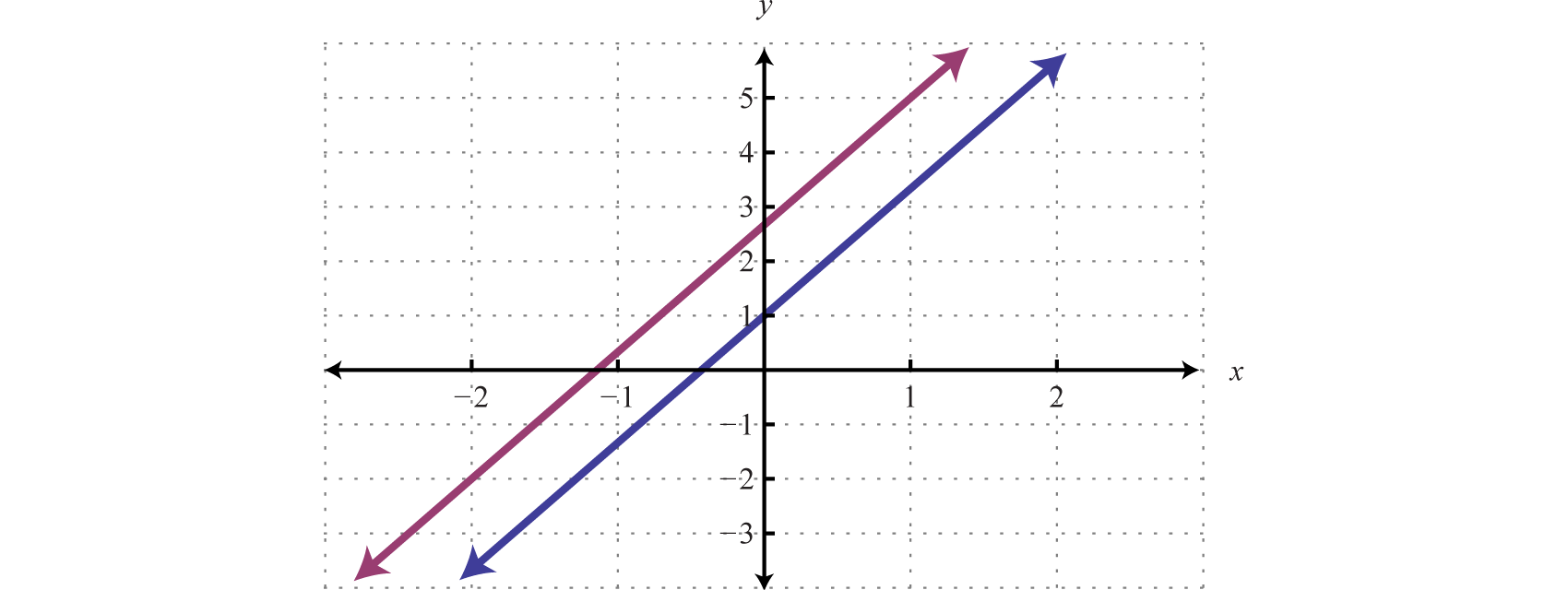
In slope-intercept form, it is easy to see that the two lines have the same slope but different y-intercepts.
The Elimination Method
In this section, the goal is to review another completely algebraic method for solving a system of linear equations called the elimination methodA means of solving a system by adding equivalent equations in such a way as to eliminate a variable. or addition methodOften used when referring to the elimination method for solving systems.. This method depends on the addition property of equationsIf A, B, C, and D are algebraic expressions, where A = B and C = D, then A + C = B + D.: given algebraic expressions A, B, C, and D we have
Consider the following system:
We can add the equations together to eliminate the variable y.
This leaves us with a linear equation with one variable that can be easily solved:
At this point, we have the x-coordinate of the simultaneous solution, so all that is left to do is back substitute to find the corresponding y-value.
The solution to the system is (3, 2). Of course, the variable is not always so easily eliminated. Typically, we have to find an equivalent system by applying the multiplication property of equality to one or both of the equations as a means to line up one of the variables to eliminate. The goal is to arrange that either the x terms or the y terms are opposites, so that when the equations are added, the terms eliminate.
Example 5
Solve by elimination: .
Solution:
We choose to eliminate the terms with variable y because the coefficients have different signs. To do this, we first determine the least common multiple of the coefficients; in this case, the LCM(3, 2) is 6. Therefore, multiply both sides of both equations by the appropriate values to obtain coefficients of −6 and 6. This results in the following equivalent system:
The terms involving y are now lined up to eliminate. Add the equations together and solve for x.
Back substitute.
Therefore the simultaneous solution is (1, 2). The check follows.
Check: (1, 2) |
|
|---|---|
Equation 1: |
Equation 2: |
Answer: (1, 2)
Sometimes linear systems are not given in standard form . When this is the case, it is best to rearrange the equations before beginning the steps to solve by elimination. Also, we can eliminate either variable. The goal is to obtain a solution for one of the variables and then back substitute to find a solution for the other.
Example 6
Solve by elimination: .
Solution:
First, rewrite the second equation in standard form.
This results in an equivalent system in standard form, where like terms are aligned in columns.
We can eliminate the term with variable x if we multiply the second equation by −4.
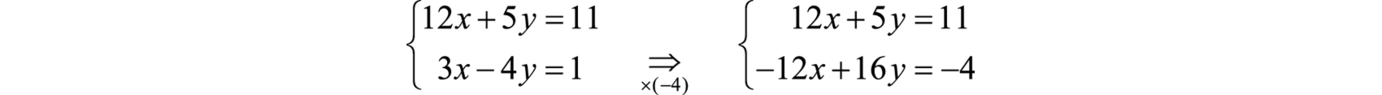
Next, we add the equations together,
Back substitute.
Answer:
At this point, we explore what happens when solving dependent and inconsistent systems using the elimination method.
Example 7
Solve by elimination: .
Solution:
To eliminate the variable x, we could multiply the first equation by −2.
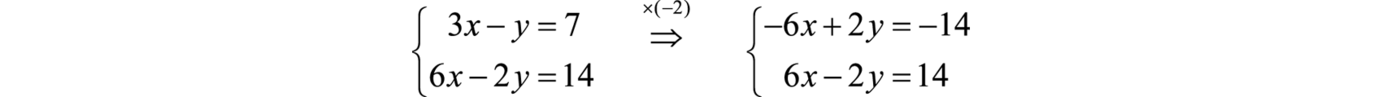
Now adding the equations we have
A true statement indicates that this is a dependent system. The lines coincide, and we need y in terms of x to present the solution set in the form . Choose one of the original equations and solve for y. Since the equations are equivalent, it does not matter which one we choose.
Answer:
Given a linear system where the equations have fractional coefficients, it is usually best to clear the fractions before beginning the elimination method.
Example 8
Solve: .
Solution:
Recall that we can clear fractions by multiplying both sides of an equation by the least common multiple of the denominators (LCD). Take care to distribute and then simplify.
Equation 1 |
Equation 2 |
This results in an equivalent system where the equations have integer coefficients,
Solve using the elimination method.
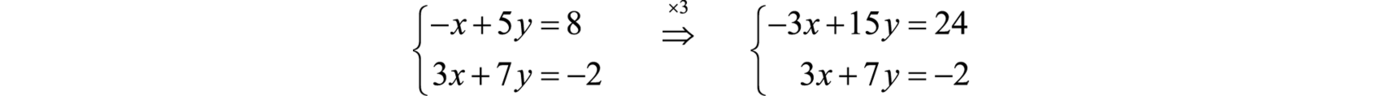
Back substitute.
Answer: (−3, 1)
We can use a similar technique to clear decimals before solving.
Summary of the Methods for Solving Linear Systems
We have reviewed three methods for solving linear systems of two equations with two variables. Each method is valid and can produce the same correct result. In this section, we summarize the strengths and weaknesses of each method.
The graphing method is useful for understanding what a system of equations is and what the solutions must look like. When the equations of a system are graphed on the same set of axes, we can see that the solution is the point where the graphs intersect. The graphing is made easy when the equations are in slope-intercept form. For example,
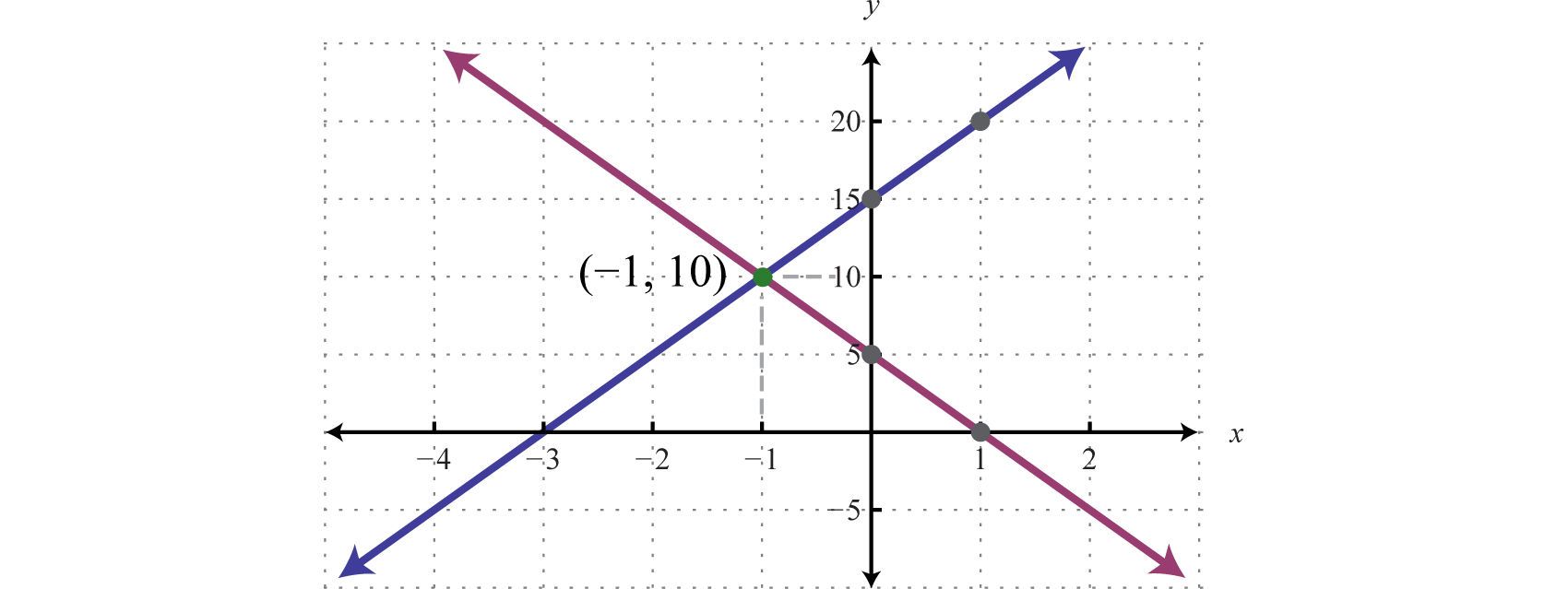
The simultaneous solution (−1, 10) corresponds to the point of intersection. One drawback of this method is that it is very inaccurate. When the coordinates of the solution are not integers, the method is practically unusable. If we have a choice, we typically avoid this method in favor of the more accurate algebraic techniques.
The substitution method, on the other hand, is a completely algebraic method. It requires you to solve for one of the variables and substitute the result into the other equation. The resulting equation has one variable for which you can solve. This method is particularly useful when there is a variable within the system with coefficient of 1. For example,
In this case, it is easy to solve for y in the first equation and then substitute the result into the other equation. One drawback of this method is that it often leads to equivalent equations with fractional coefficients, which are tedious to work with. If there is not a coefficient of 1, then it usually is best to choose the elimination method.
The elimination method is a completely algebraic method which makes use of the addition property of equations. We multiply one or both of the equations to obtain equivalent equations where one of the variables is eliminated if we add them together. For example,
To eliminate the terms involving x, we would multiply both sides of the first equation by 5 and both sides of the second equation by −2. This results in an equivalent system where the variable x is eliminated when we add the equations together. Of course, there are other combinations of numbers that achieve the same result. We could even choose to eliminate the variable y. No matter which variable is eliminated first, the solution will be the same. Note that the substitution method, in this case, would require tedious calculations with fractional coefficients. One weakness of the elimination method, as we will see later in our study of algebra, is that it does not always work for nonlinear systems.
Key Takeaways
- The substitution method requires that we solve for one of the variables and then substitute the result into the other equation. After performing the substitution step, the resulting equation has one variable and can be solved using the techniques learned up to this point.
- The elimination method is another completely algebraic method for solving a system of equations. Multiply one or both of the equations in a system by certain numbers to obtain an equivalent system where at least one variable in both equations have opposite coefficients. Adding these equivalent equations together eliminates that variable, and the resulting equation has one variable for which you can solve.
- It is a good practice to first rewrite the equations in standard form before beginning the elimination method.
- Solutions to systems of two linear equations with two variables, if they exist, are ordered pairs (x, y).
- If the process of solving a system of equations leads to a false statement, then the system is inconsistent and there is no solution, .
- If the process of solving a system of equations leads to an identity, then the system is dependent and there are infinitely many solutions that can be expressed using the form .
Topic Exercises
Part A: Substitution Method
Solve by substitution.
Part B: Elimination Method
Solve by elimination.
Part C: Mixed Practice
Solve using any method.
-
Explain to a beginning algebra student how to choose a method for solving a system of two linear equations. Also, explain what solutions look like and why.
-
Make up your own linear system with two variables and solve it using all three methods. Explain which method was preferable in your exercise.
Part D: Discussion Board
Answers
-
(−2, 11)
-
-
(2, 2)
-
-
-
-
-
-
(4, −2)
-
-
(3, −2)
-
-
(3, −4)
-
-
-
-
-
-
-
-
(2, −3)
-
-
-
-
-
-
(1, 1)
-
-
-
-
-
-
(0, 0)
-
-
(1, 2)
-
-
-
-
-
-
(−4, 2)
-
-
(−8, −1)
-
-
-
-
-
-
-
-
(−1, −2)
-
-
(−28, 0)
-
-
-
-
(1, 2)
-
-
(−1, −4)
-
-
(−5, 2)
-
-
-
-
-
-
-
-
(120, 77)
-
-
-
-
-
-
(0.5, −3)
-
-
-
-
-
-
-
-
(−2, −10)
-
-
(3, −1)
-
-
(32, 0)
-
-
-
-
(−4, 3)
-
-
-
-
-
-
(0.8, −5.4)
-
-
Ø
-
-
Answer may vary
-




