This is “Review Exercises and Sample Exam”, section 2.8 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
2.8 Review Exercises and Sample Exam
Review Exercises
-
{(−4, −1), (−5, 3), (10, 3), (11, 2), (15, 1)}
-
{(−3, 0), (−2, 1), (1, 3), (2, 7), (2, 5)}
-
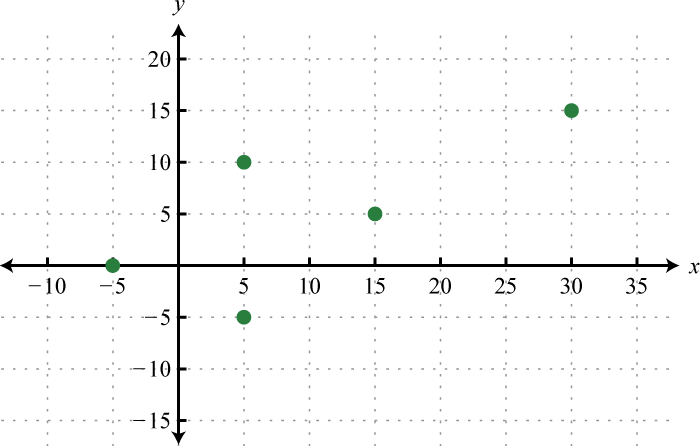
-

-
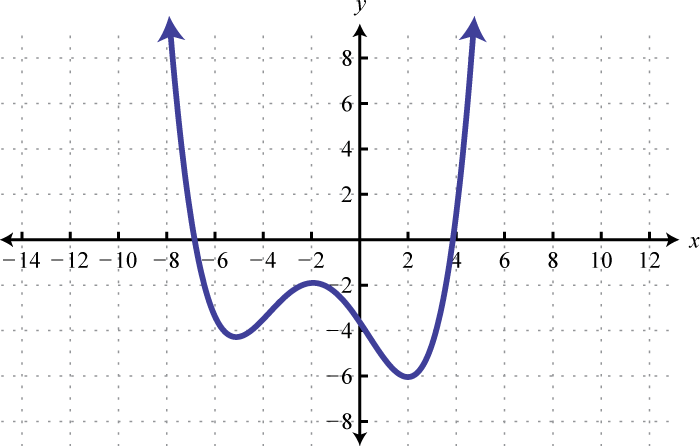
-
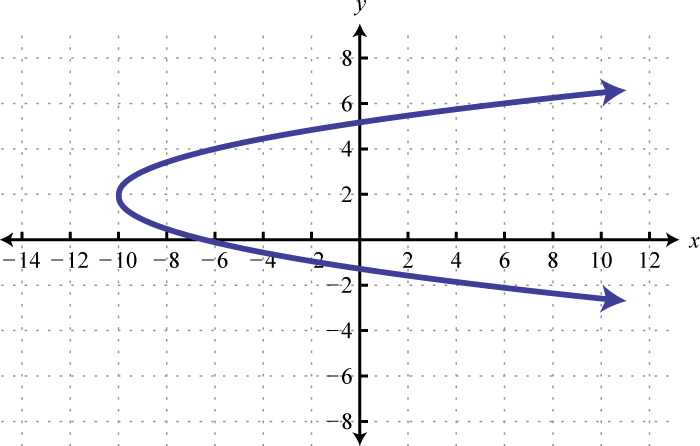
-
-
-
; , , and
-
; , , and
-
; find , , and
-
; find , , and
-
; find , ,
-
; find , , and
-
; find x where
-
; find x where
-
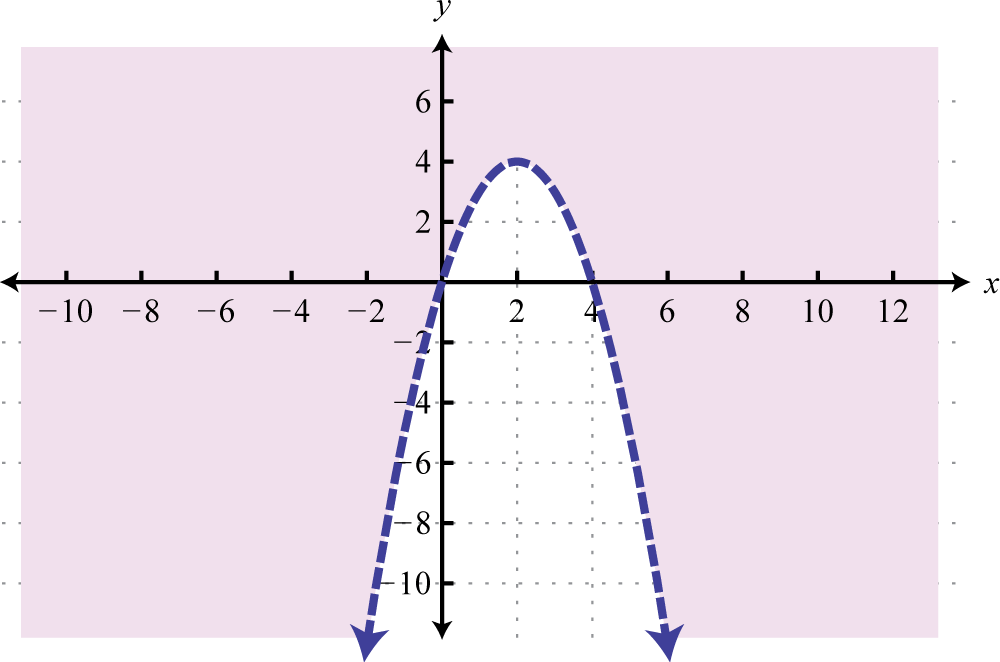
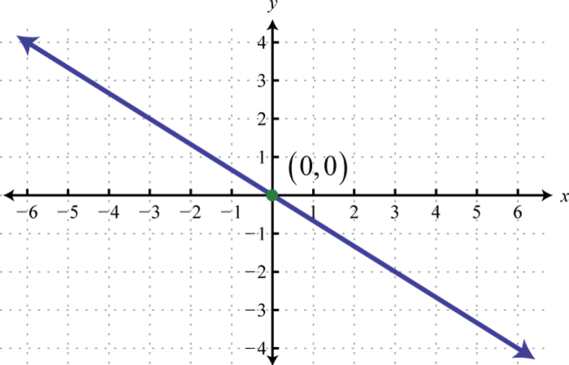
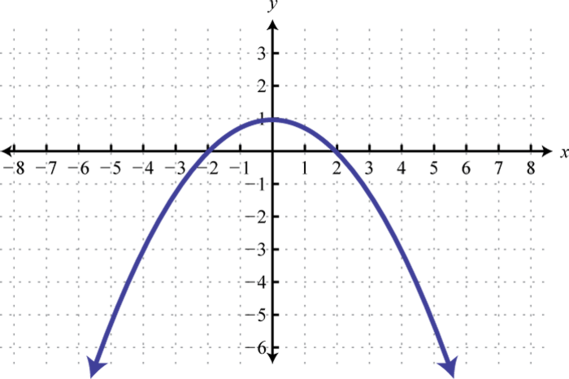
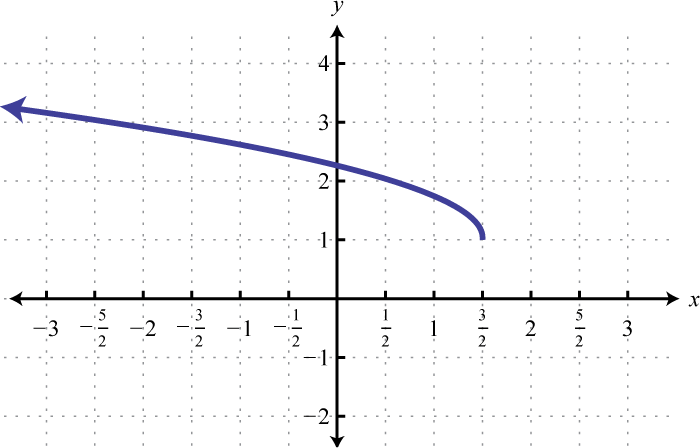
Given the graph of below, find , , and
-
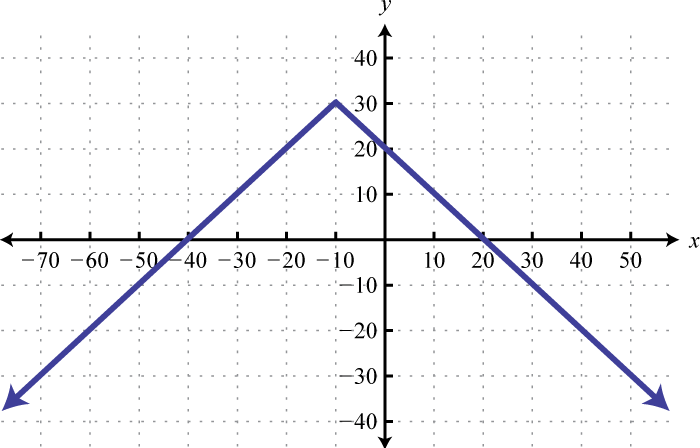
Given the graph of below, find x where and
Relations, Graphs, and Functions
Determine the domain and range and state whether the function is a relation or not.
Evaluate.
-
-
-
-
-
-
-
-
-
-
-
and
-
and
-
and
-
and
-
and
-
and
-
, ;
-
, ;
-
, ;
-
, ;
Linear Functions and Their Graphs
Graph and label the intercepts.
Graph the linear function and label the x-intercept.
Find the slope of the line passing through the given points.
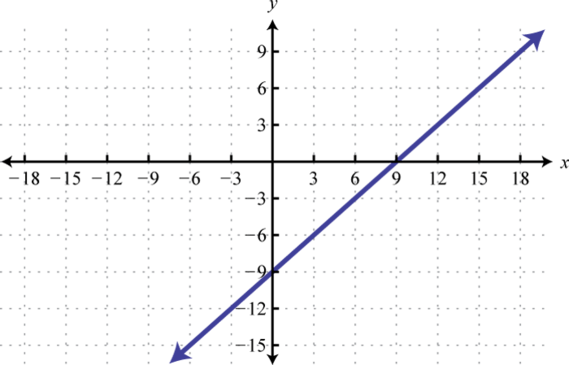
Graph and on the same rectangular coordinate plane. Use the graph to find all values of x for which the given relation is true. Verify your answer algebraically.
-
and
-
and
-
and
-
and
-
Find the equation of the given linear function:
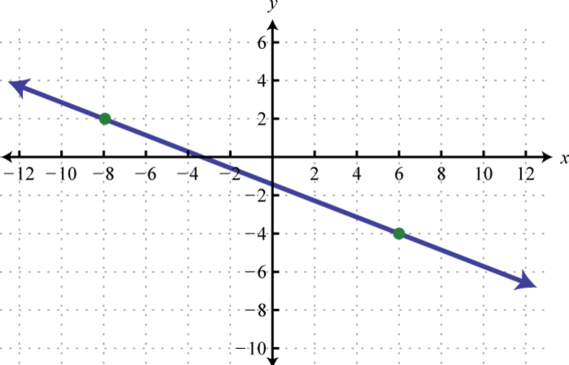
-
Find the equation of the given linear function:
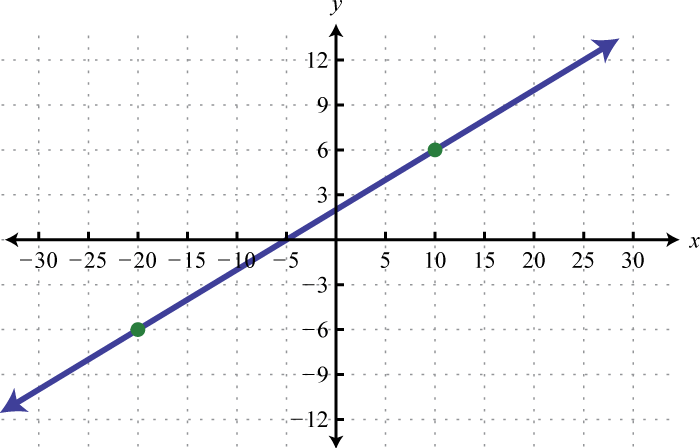
-
Parallel to and passing through
-
Parallel to and passing through
-
Parallel to and passing through
-
Perpendicular to and passing through
-
Perpendicular to and passing through
-
Perpendicular to and passing through
-
A taxi fare in a certain city includes an initial charge of $2.50 plus $2.00 per mile driven. Write a function that gives the cost of a taxi ride in terms of the number of miles driven. Use the function to determine the number of miles driven if the total fare is $9.70.
-
A salesperson earns a base salary of $1,800 per month and 4.2% commission on her total sales for that month. Write a function that gives her monthly salary based on her total sales. Use the function to determine the amount of sales for a month in which her salary was $4,824.
-
A certain automobile sold for $1,200 in 1980, after which it began to be considered a collector’s item. In 1994, the same automobile sold at auction for $5,750. Write a linear function that models the value of the automobile in terms of the number of years since 1980. Use it to estimate the value of the automobile in the year 2000.
-
A specialized industrial robot was purchased new for $62,400. It has a lifespan of 12 years, after which it will be considered worthless. Write a linear function that models the value of the robot. Use the function to determine its value after 8 years of operation.
-
In 1950, the U.S. Census Bureau estimated the population of Detroit, MI to be 1.8 million people. In 1990, the population was estimated to have decreased to 1 million. Write a linear function that gives the population of Detroit in millions of people, in terms of years since 1950. Use the function to estimate the year in which the population decreased to 700,000 people.
-
Online sales of a particular product are related to the number of clicks on its advertisement. It was found that 100 clicks in a week result in $112 of online sales, and that 500 clicks result in $160 of online sales. Write a linear function that models the online sales of the product based on the number of clicks on its advertisement. How many clicks are needed to result in $250 of weekly online sales from this product?
-
The cost in dollars of producing n bicycles is given by the formula If each bicycle can be sold for $132, write a function that gives the profit generated by producing and selling n bicycles. Use the formula to determine the number of bicycles that must be produced and sold to profit at least $10,000.
-
Determine the breakeven point from the previous exercise.
Modeling Linear Functions
Find the linear function passing through the given points.
Find the equation of the line:
Use algebra to solve the following.
-
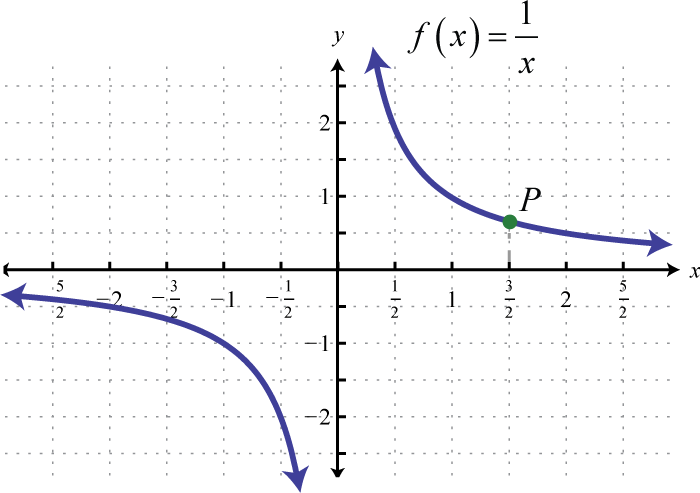
-
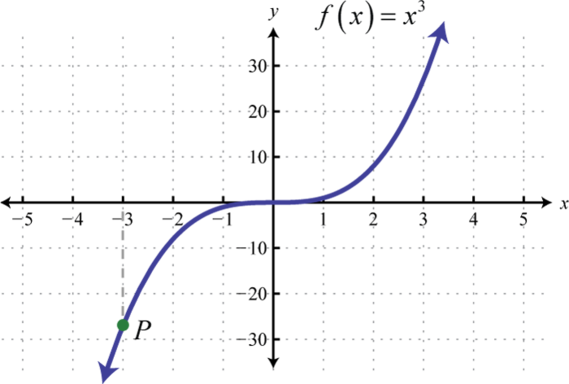
-
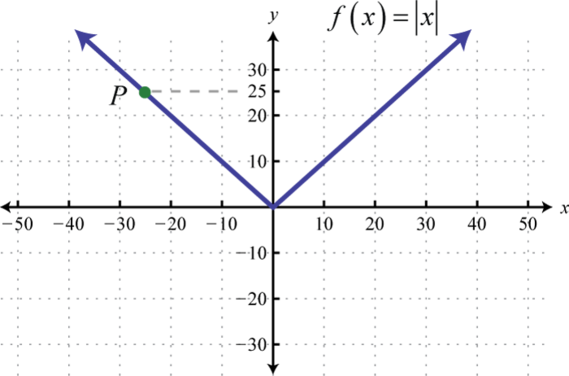
-
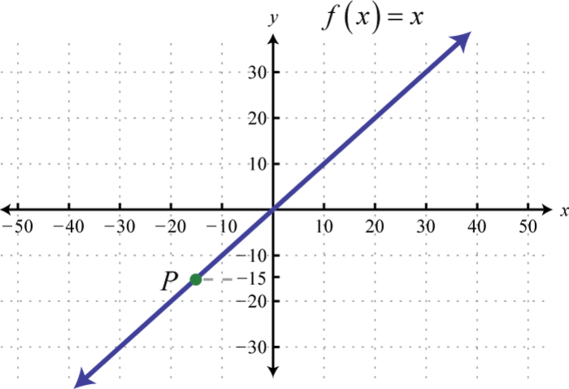
-
-
-
-
-
-
-
-
-
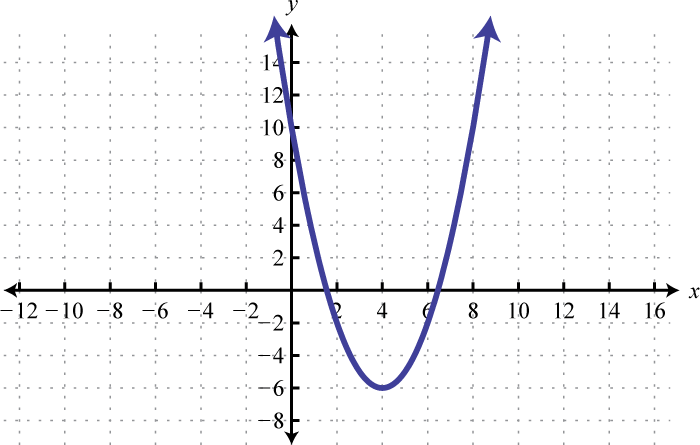
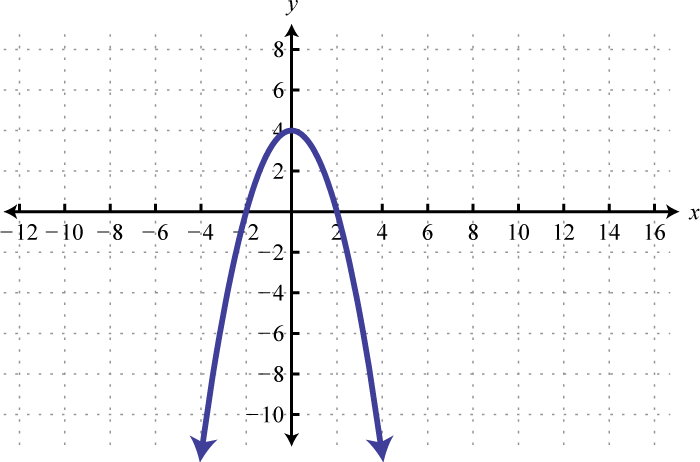
Find , , and
-
Find , , and
-
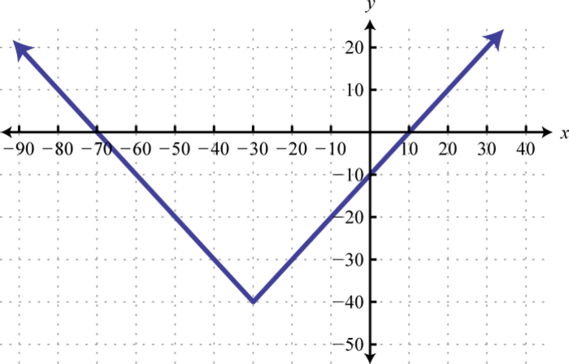
Find , and
-
Find , and
Basic Functions
Find the ordered pair that specifies the point P.
Graph the piecewise defined functions.
Evaluate.
Transformations
Sketch the graph of the given function.
Write an equation that represents the function whose graph is given.
Solving Absolute Value Equations and Inequalities
Solve.
Solve. Graph the solutions on a number line and give the corresponding interval notation.
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
-
-
-
-
-
-
-
-
-
-
-
Inequalities with Two Variables
Is the ordered pair a solution to the given inequality?
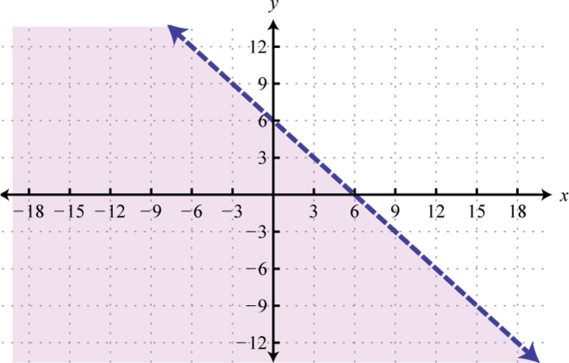
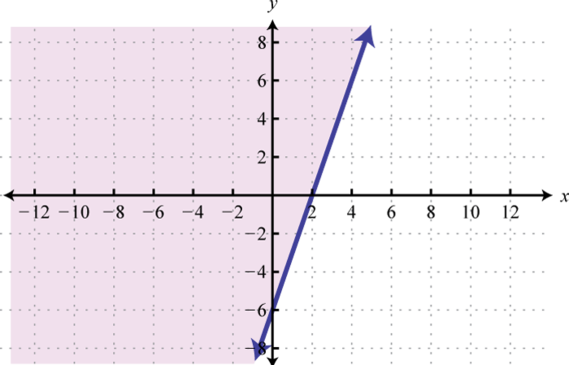
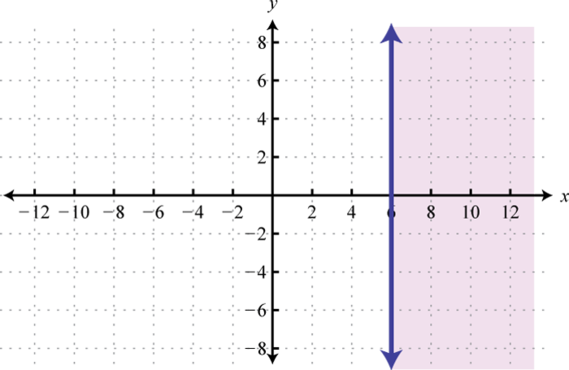
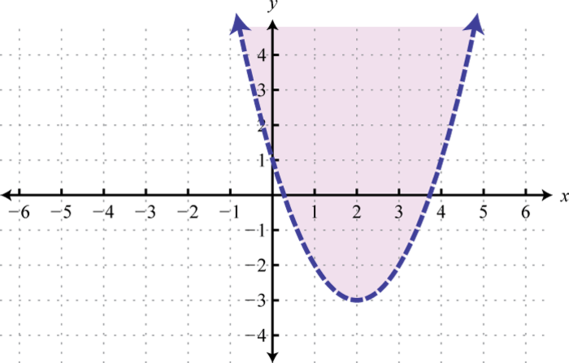
Graph the solution set.
Answers
-
Domain: {−5, −4, 10, 11, 15}; range:{−1, 1, 2, 3}; function: yes
-
-
Domain: {−5, 5, 15, 30}; range: {−5, 0, 5, 10, 15}; function: no
-
-
Domain: ; range: ; function: yes
-
-
Domain: ; range: ; function: yes
-
-
, , and
-
-
, , and
-
-
, ,
-
-
-
-
, ,
-
-
-
-
-
-
-
-
-
-
-
-
-
-
; 3.6 miles
-
-
; $7,700
-
-
; 2005
-
-
; 258 bicycles
-
-
-
-
-
-
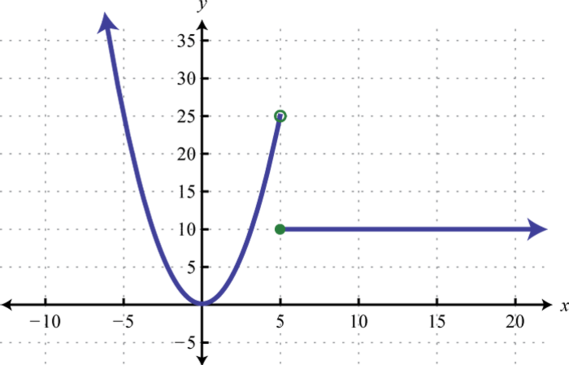
-
-
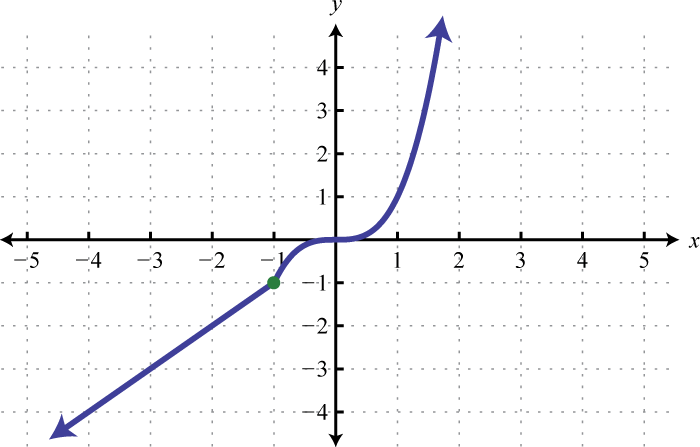
-
-
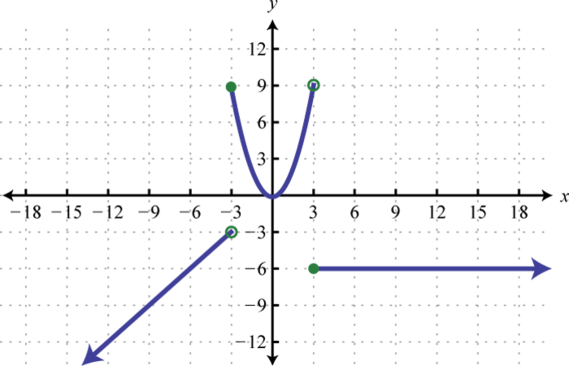
-
-
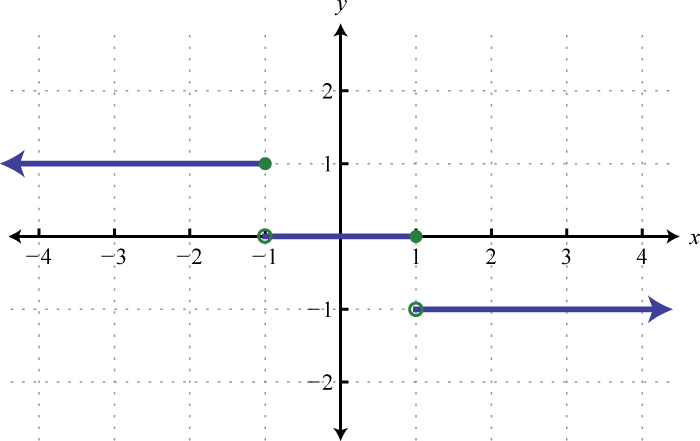
-
-
, ,
-
-
, ,
-
-
−2,
-
-
3, 5
-
-
2
-
-
−1,
-
-
−12,
-
-
;
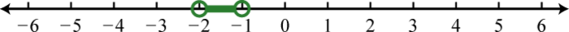
-
-
;

-
-
;

-
-
Ø;
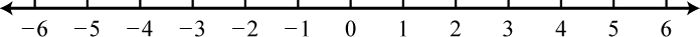
-
-
;

-
-
Yes
-
-
Yes
-
-
Yes
-
-
No
-
-
-
-
-
-
-
-
-
-
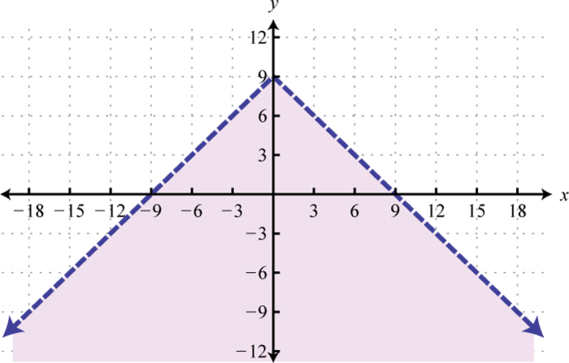
-
-
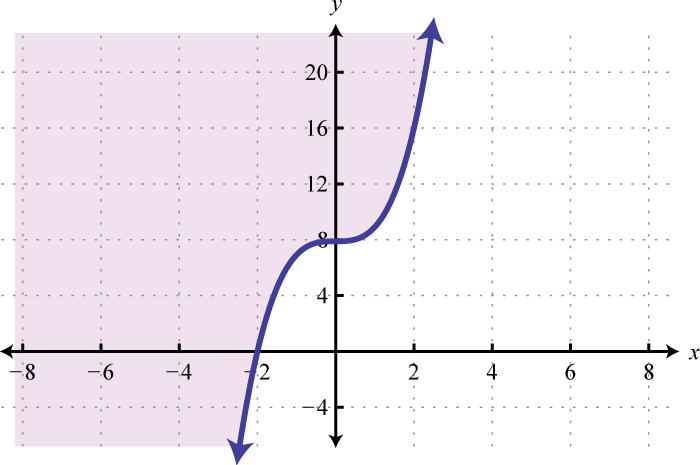
-
Sample Exam
-
Determine whether or not the following graph represents a function or not. Explain.
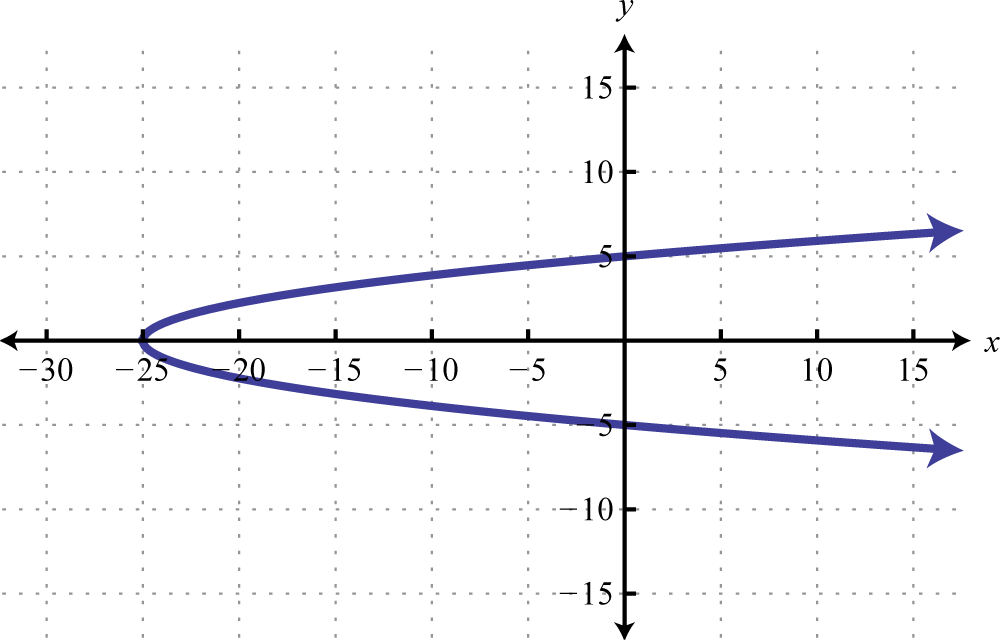
-
Determine the domain and range of the following function.
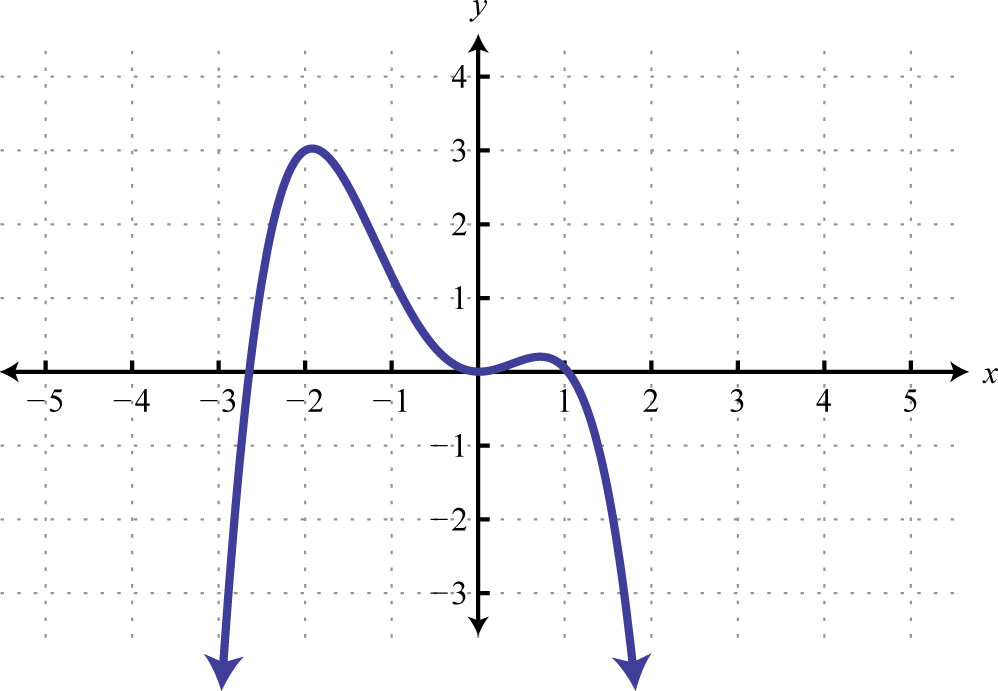
-
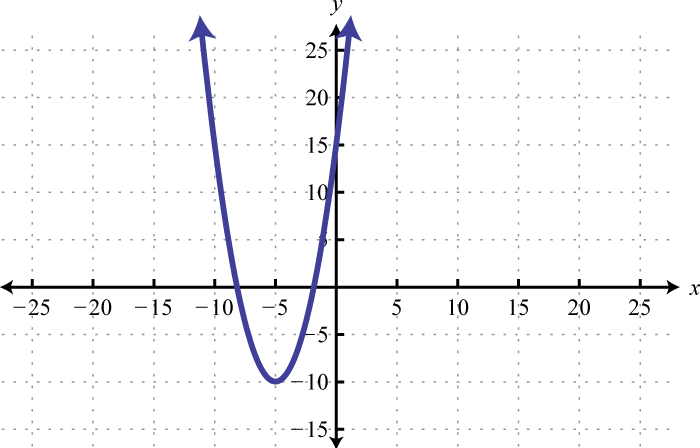
Given , find , , and
-
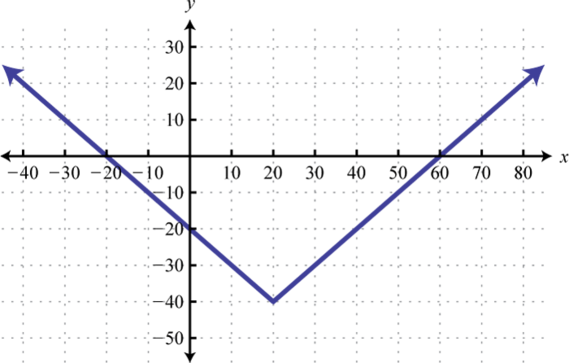
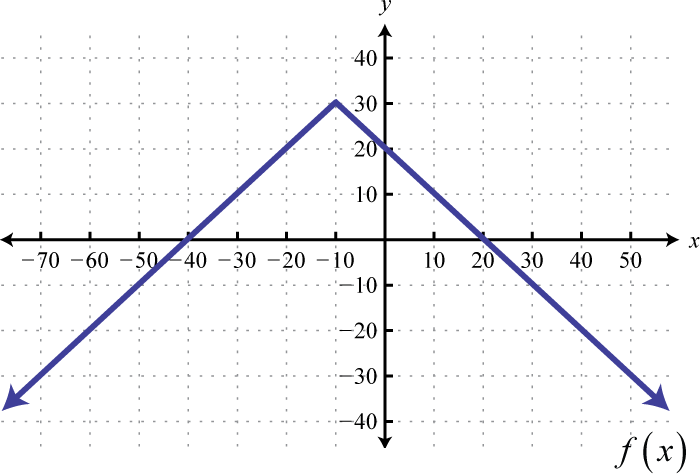
Given the graph of a function :
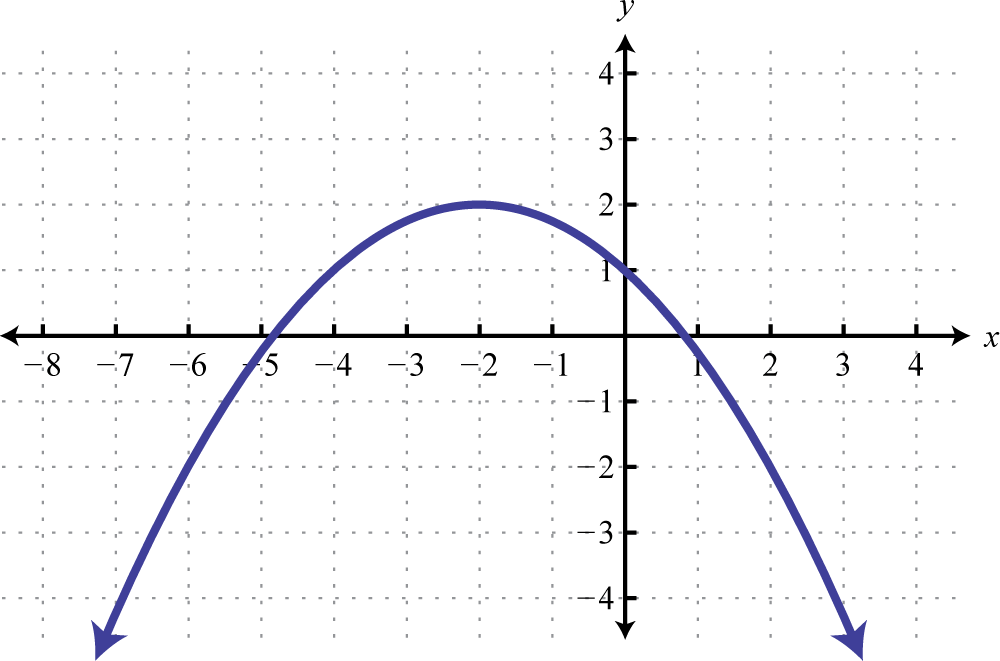
- Find , , and
- Find x where
-
Graph and label the x-intercept.
-
Find a linear function passing through and
-
Find the equation of the line parallel to and passing through
-
Find the equation of the line perpendicular to and passing through
-
The annual revenue of a new web-services company in dollars is given by where n represents the number of users the company has registered. The annual maintenance cost of the company’s registered user base in dollars is given by the formula where n represents the users.
- Write a function that models the annual profit based on the number of registered users.
- Determine the number of registered users needed to break even.
-
A particular search engine assigns a ranking to a webpage based on the number of links that direct users to the webpage. If no links are found, the webpage is assigned a ranking of 1. If 40 links are found directing users to the webpage, the search engine assigns a page ranking of 5.
- Find a linear function that gives the webpage ranking based on the number of links that direct users to it.
- How many links will be needed to obtain a page ranking of 7?
-
-
-
-
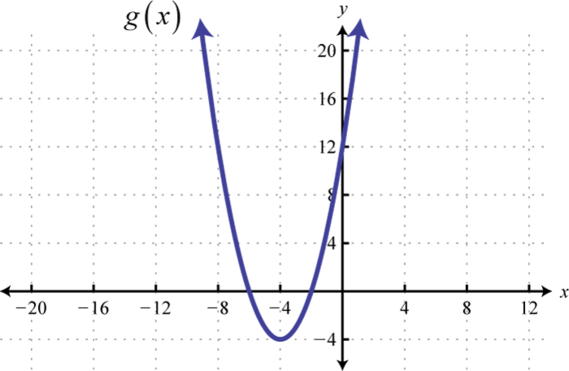
Given the graph, determine the function definition and its domain and range:
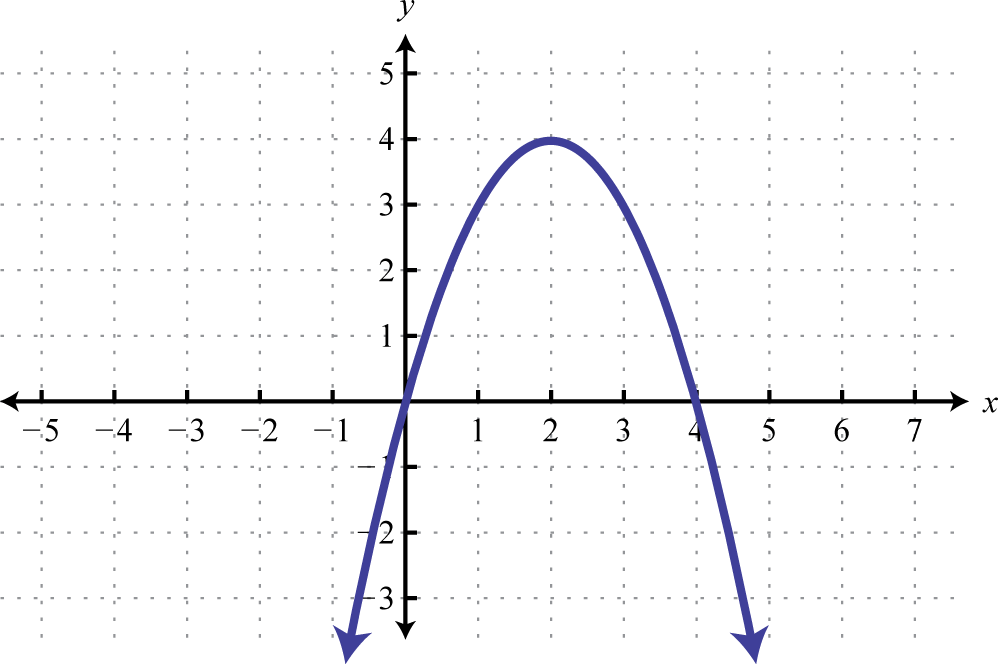
-
Sketch the graph:
-
Sketch the graph:
-
-
-
-
-
-
-
-
-
Use the transformations to sketch the graph of the following functions and state the domain and range.
Solve.
Solve and graph the solution set.
Graph the solution set.
Answers
-
The graph is not a function; it fails the vertical line test.
-
-
, , and
-
-
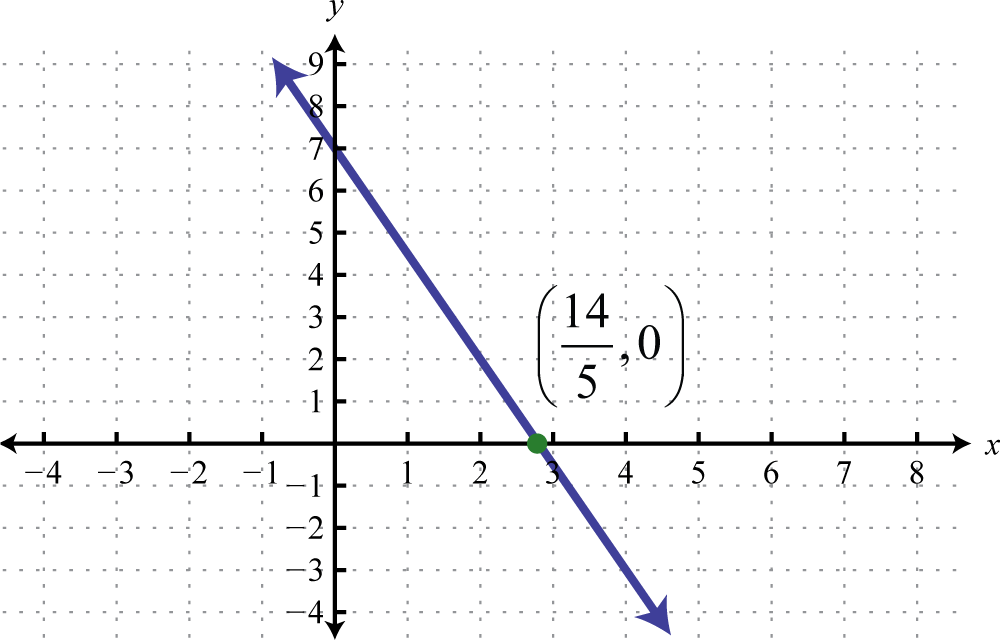
-
-
-
-
- ;
- 562 users
-
-
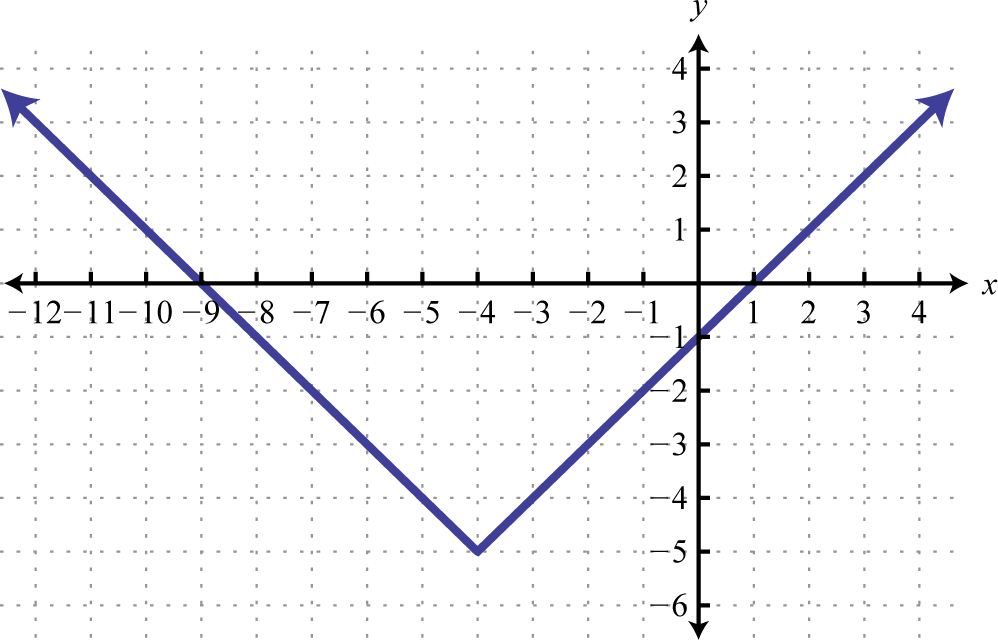
Domain: ; range:
-
-
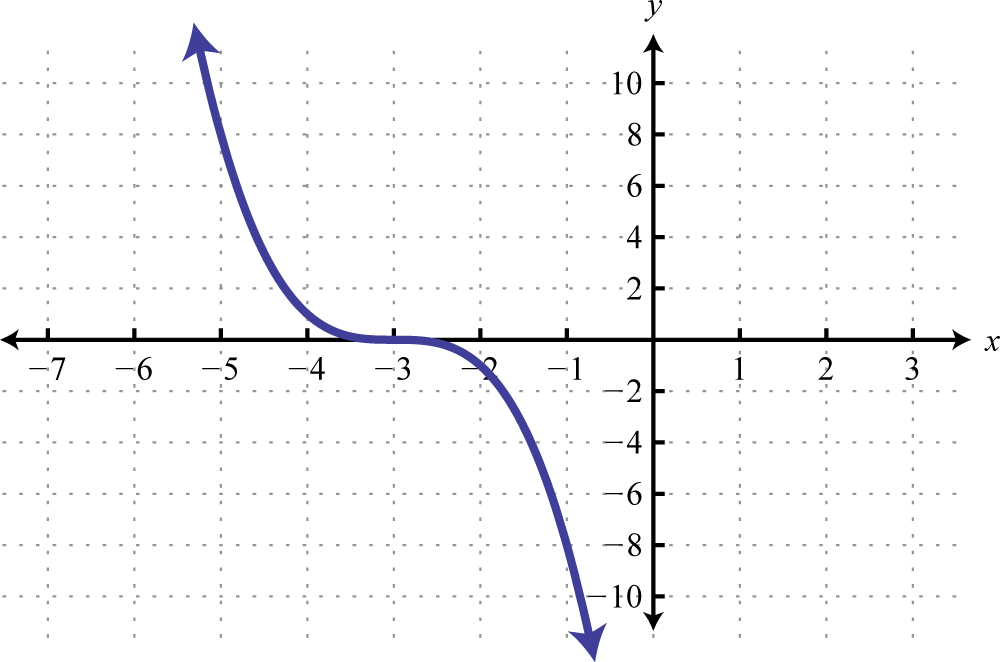
Domain: ; range:
-
-
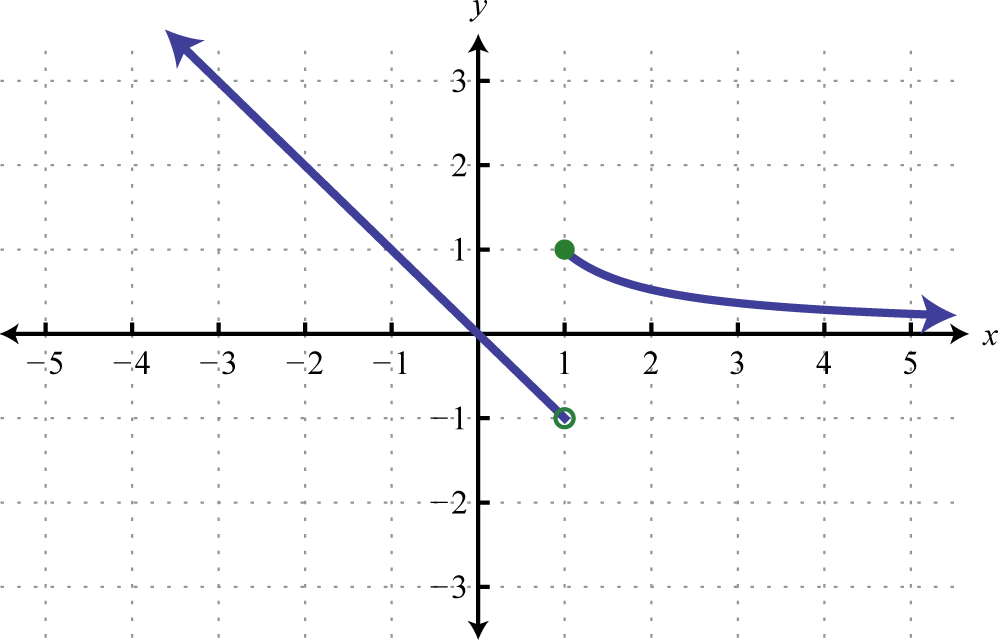
-
-
−2, 3
-
-
-
-
;

-
-
Ø;
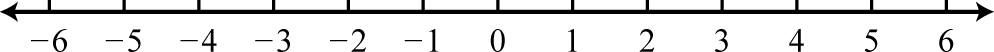
-
-