This is “Graphing the Basic Functions”, section 2.4 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
2.4 Graphing the Basic Functions
Learning Objectives
- Define and graph seven basic functions.
- Define and graph piecewise functions.
- Evaluate piecewise defined functions.
- Define the greatest integer function.
Basic Functions
In this section we graph seven basic functions that will be used throughout this course. Each function is graphed by plotting points. Remember that and thus and y can be used interchangeably.
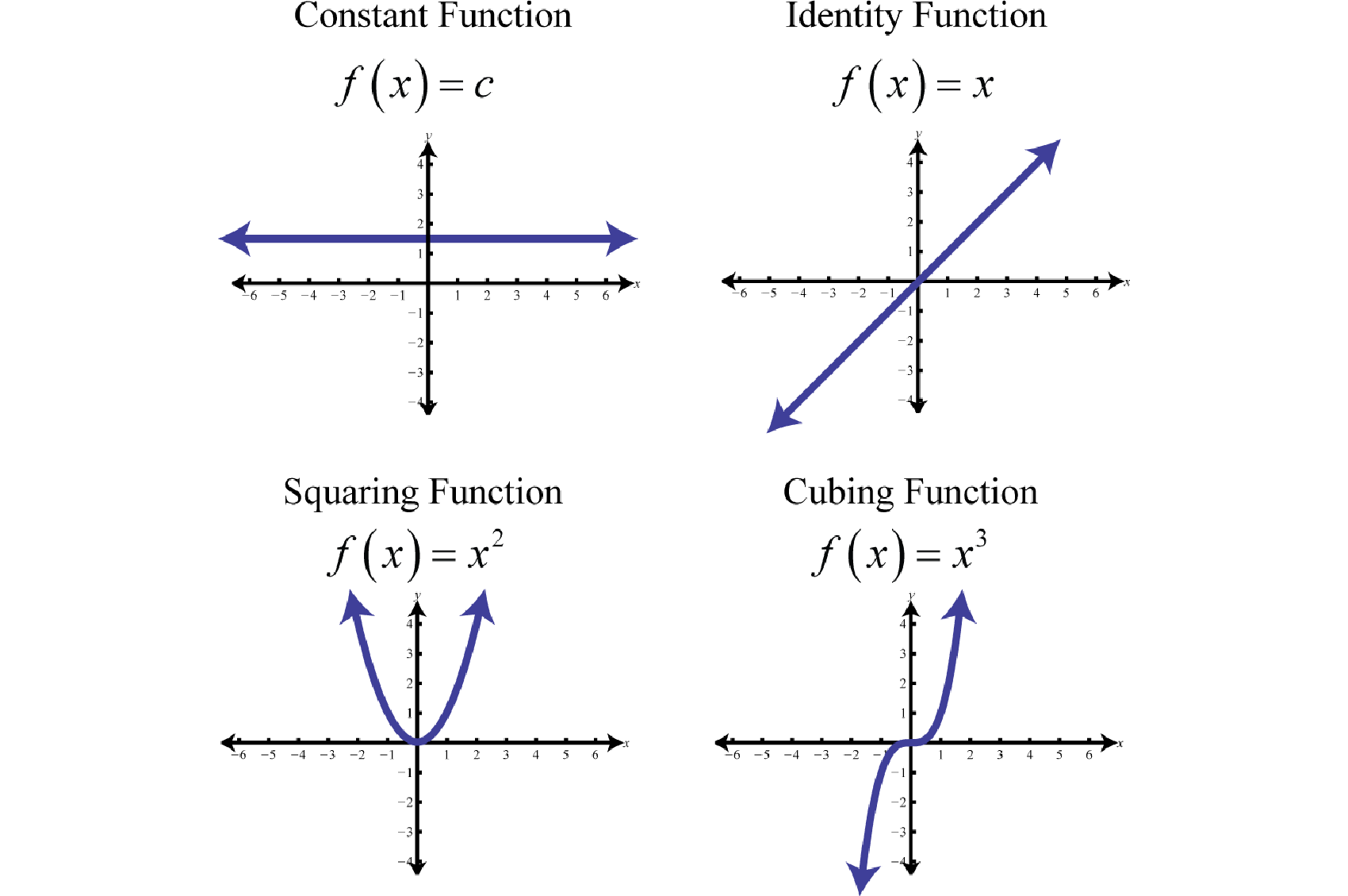
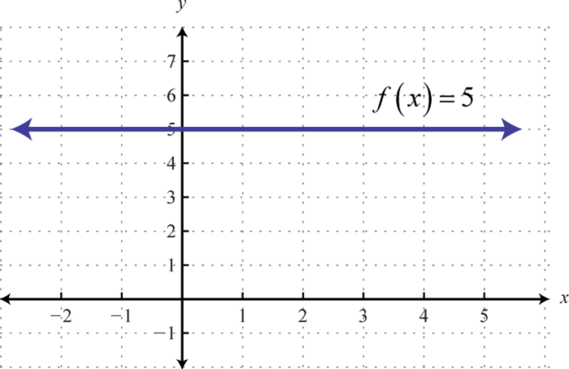
Any function of the form , where c is any real number, is called a constant functionAny function of the form where c is a real number.. Constant functions are linear and can be written In this form, it is clear that the slope is 0 and the y-intercept is Evaluating any value for x, such as x = 2, will result in c.
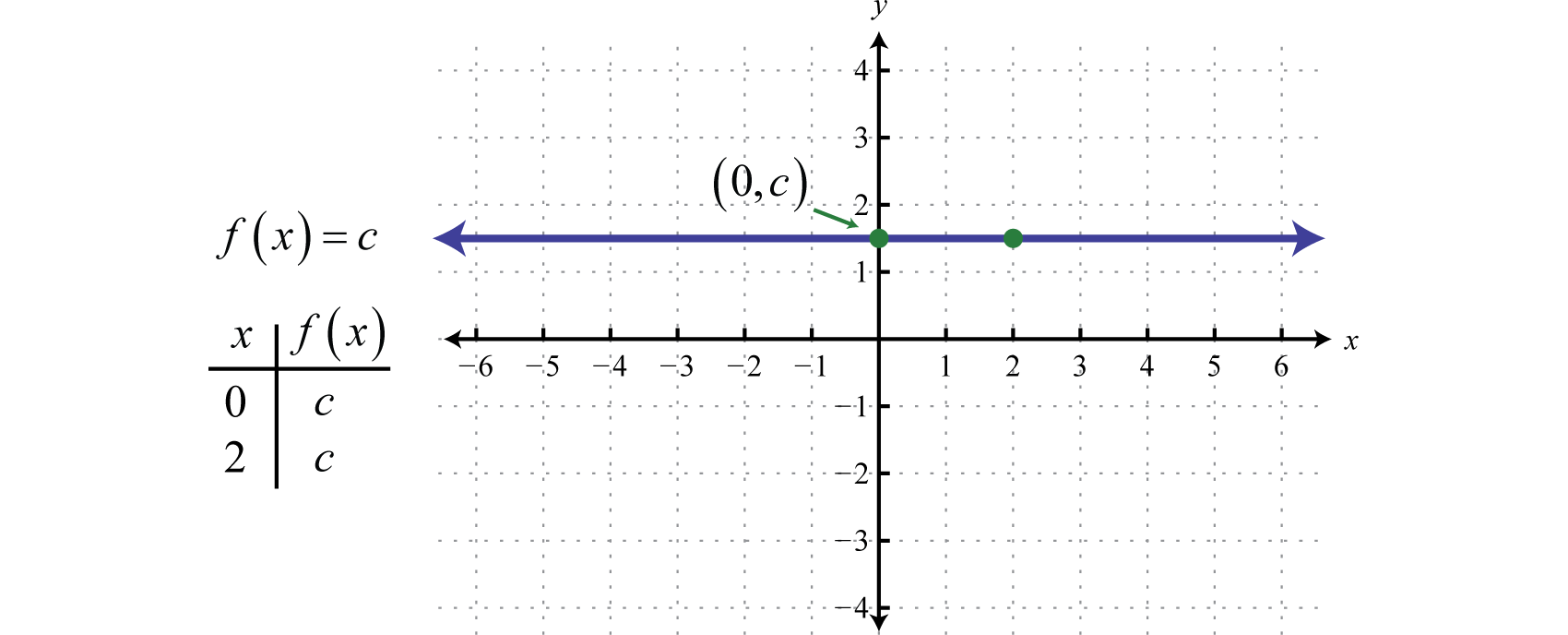
The graph of a constant function is a horizontal line. The domain consists of all real numbers and the range consists of the single value {c}.
We next define the identity functionThe linear function defined by Evaluating any value for x will result in that same value. For example, and The identity function is linear, , with slope and y-intercept (0, 0).
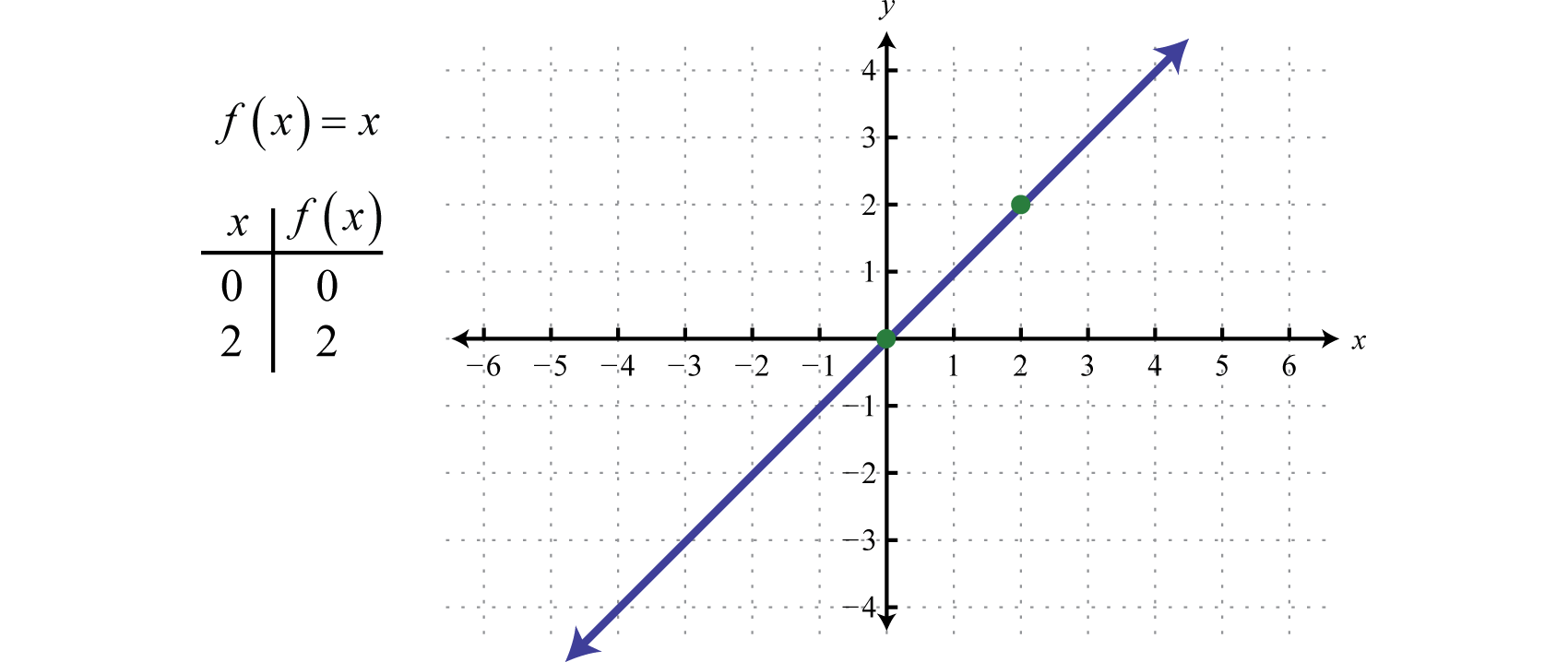
The domain and range both consist of all real numbers.
The squaring functionThe quadratic function defined by , defined by , is the function obtained by squaring the values in the domain. For example, and The result of squaring nonzero values in the domain will always be positive.
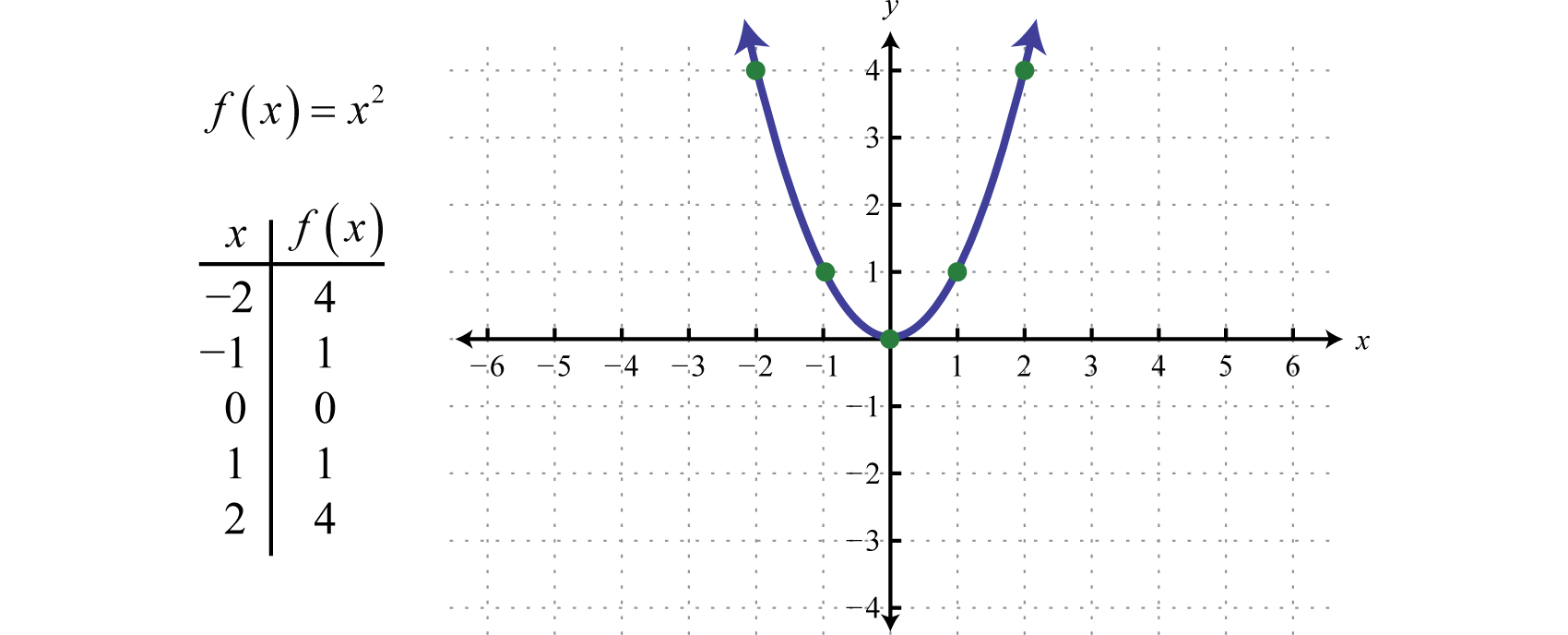
The resulting curved graph is called a parabolaThe curved graph formed by the squaring function.. The domain consists of all real numbers and the range consists of all y-values greater than or equal to zero
The cubing functionThe cubic function defined by , defined by , raises all of the values in the domain to the third power. The results can be either positive, zero, or negative. For example, , , and
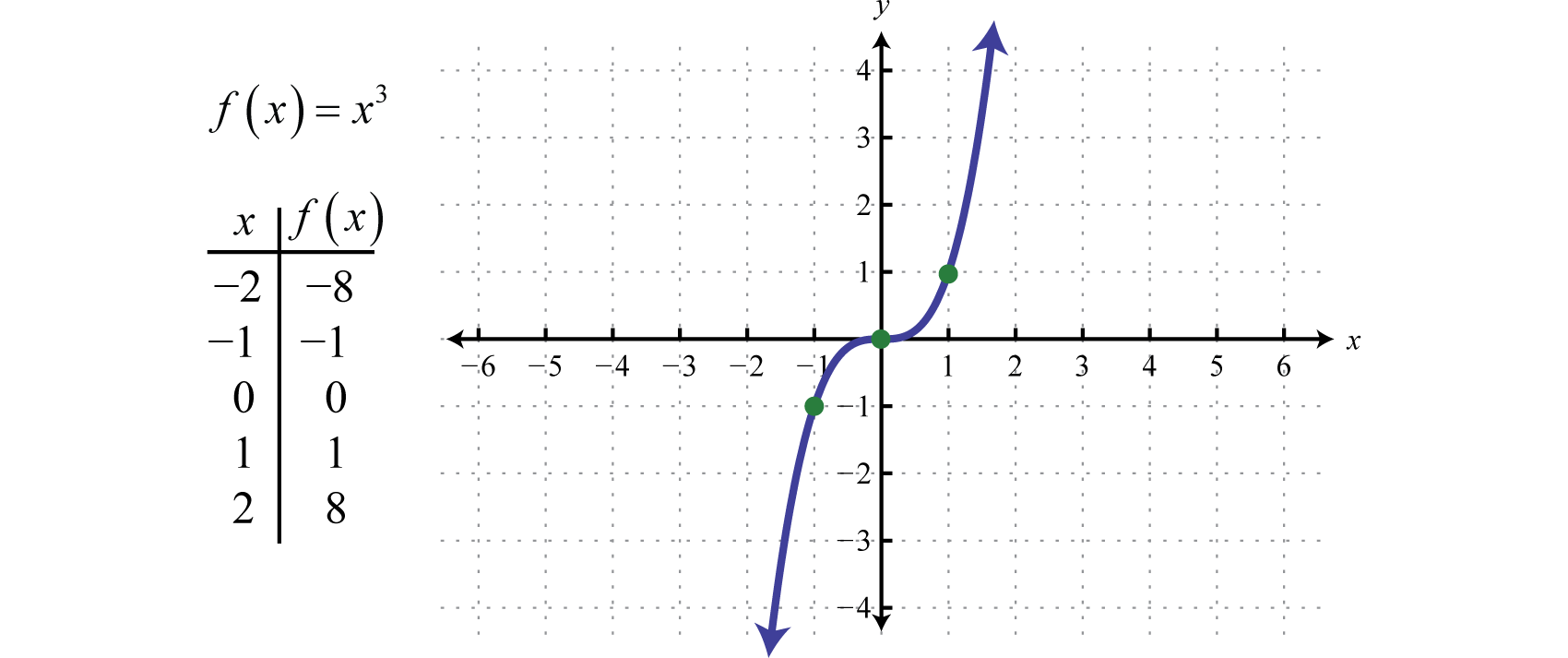
The domain and range both consist of all real numbers
Note that the constant, identity, squaring, and cubing functions are all examples of basic polynomial functions. The next three basic functions are not polynomials.
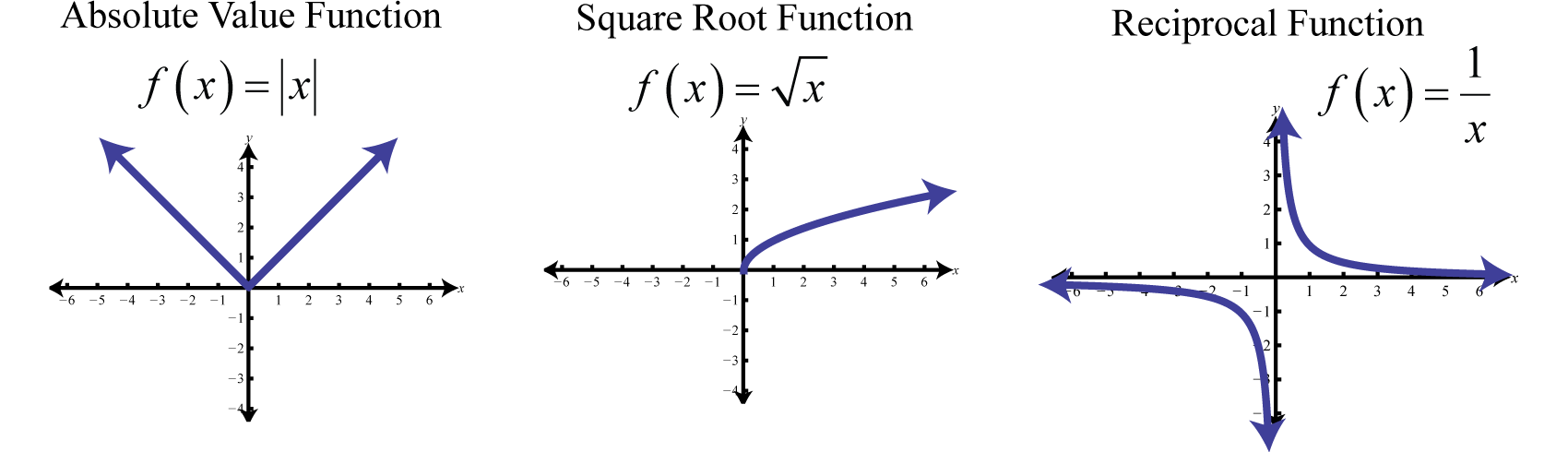
The absolute value functionThe function defined by , defined by , is a function where the output represents the distance to the origin on a number line. The result of evaluating the absolute value function for any nonzero value of x will always be positive. For example, and

The domain of the absolute value function consists of all real numbers and the range consists of all y-values greater than or equal to zero
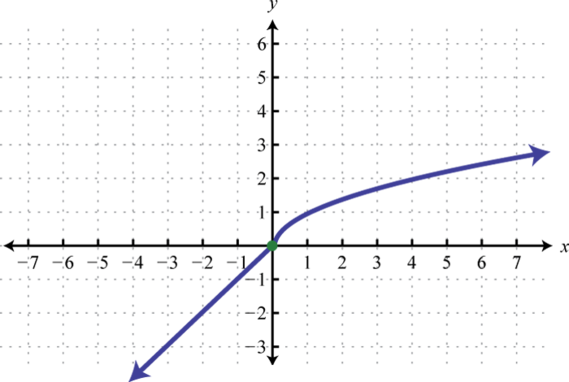
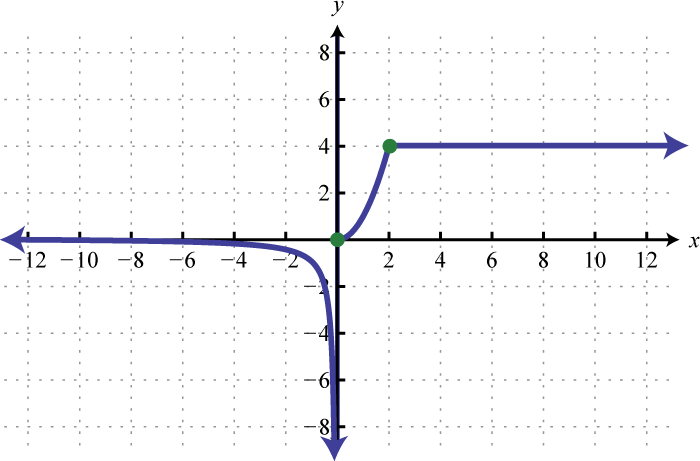
The square root functionThe function defined by , defined by , is not defined to be a real number if the x-values are negative. Therefore, the smallest value in the domain is zero. For example, and
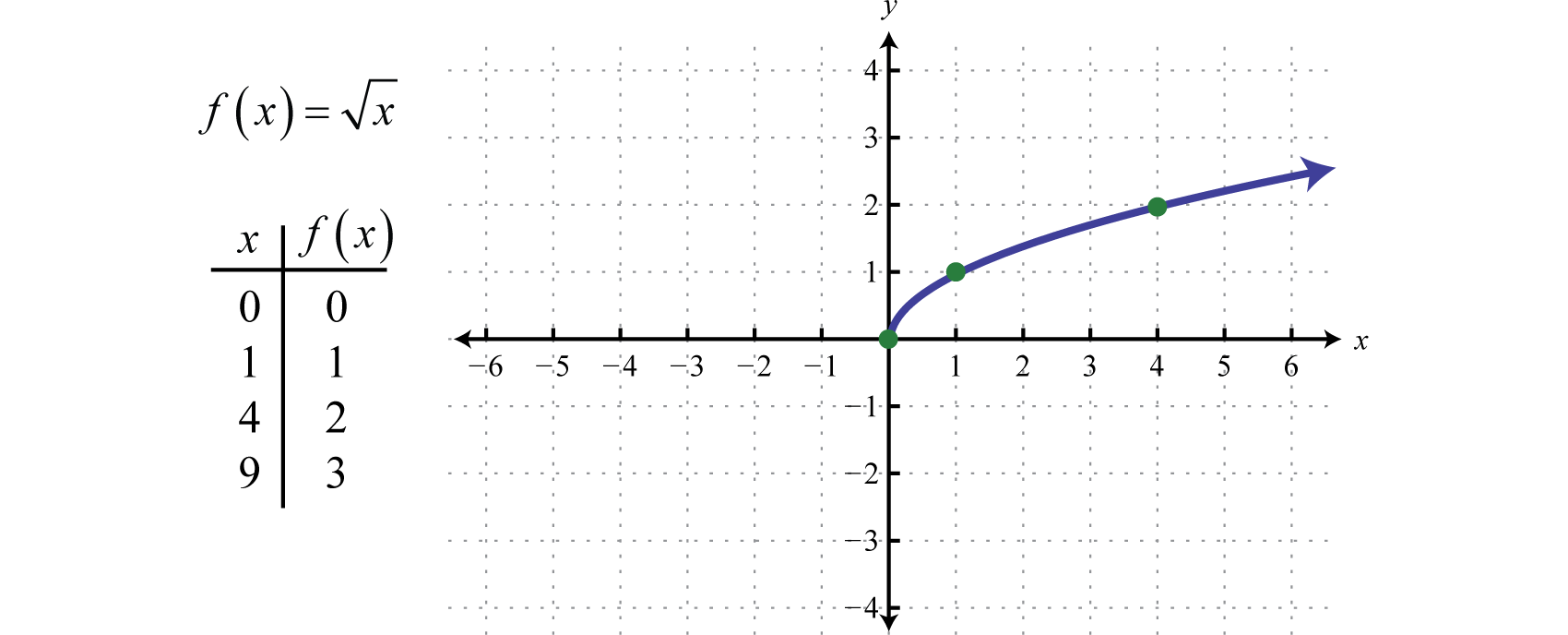
The domain and range both consist of real numbers greater than or equal to zero
The reciprocal functionThe function defined by , defined by , is a rational function with one restriction on the domain, namely The reciprocal of an x-value very close to zero is very large. For example,
In other words, as the x-values approach zero their reciprocals will tend toward either positive or negative infinity. This describes a vertical asymptoteA vertical line to which a graph becomes infinitely close. at the y-axis. Furthermore, where the x-values are very large the result of the reciprocal function is very small.
In other words, as the x-values become very large the resulting y-values tend toward zero. This describes a horizontal asymptoteA horizontal line to which a graph becomes infinitely close where the x-values tend toward ±∞. at the x-axis. After plotting a number of points the general shape of the reciprocal function can be determined.
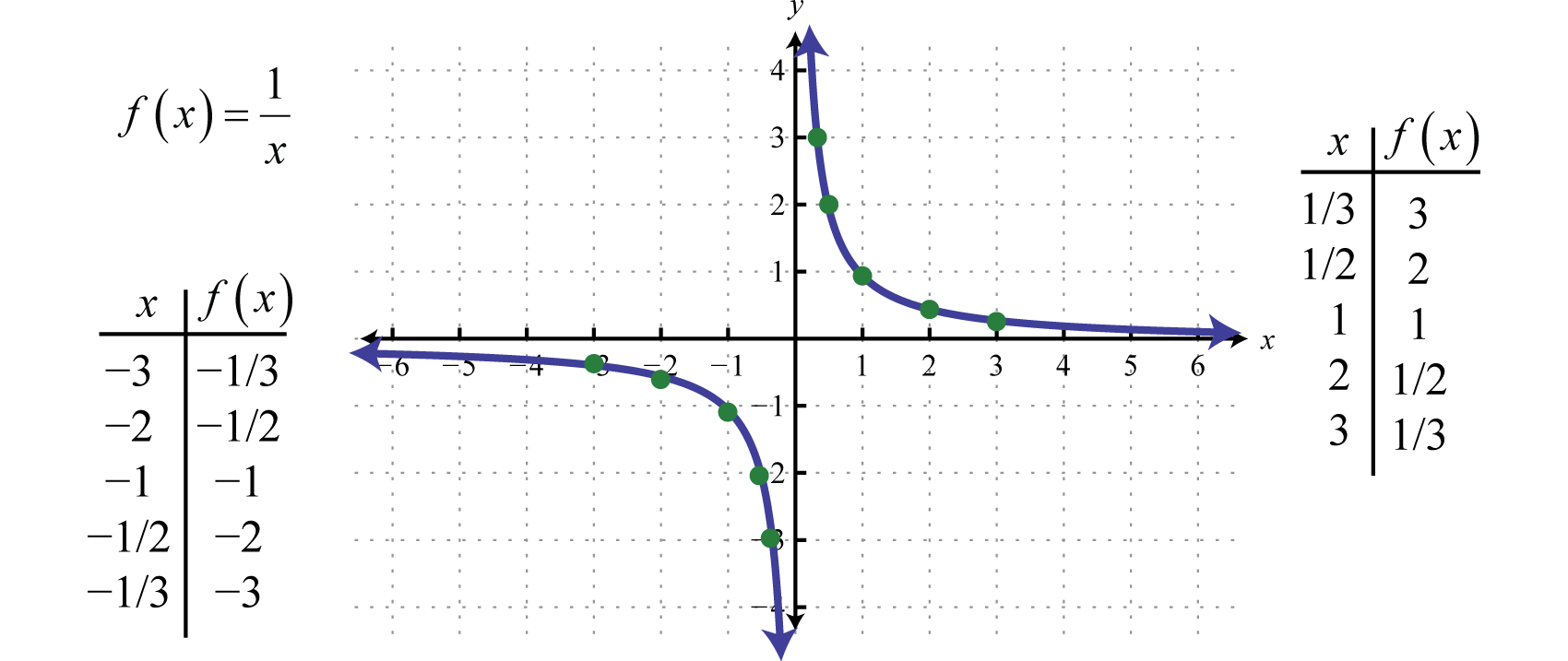
Both the domain and range of the reciprocal function consists of all real numbers except 0, which can be expressed using interval notation as follows:
In summary, the basic polynomial functions are:
The basic nonpolynomial functions are:
Piecewise Defined Functions
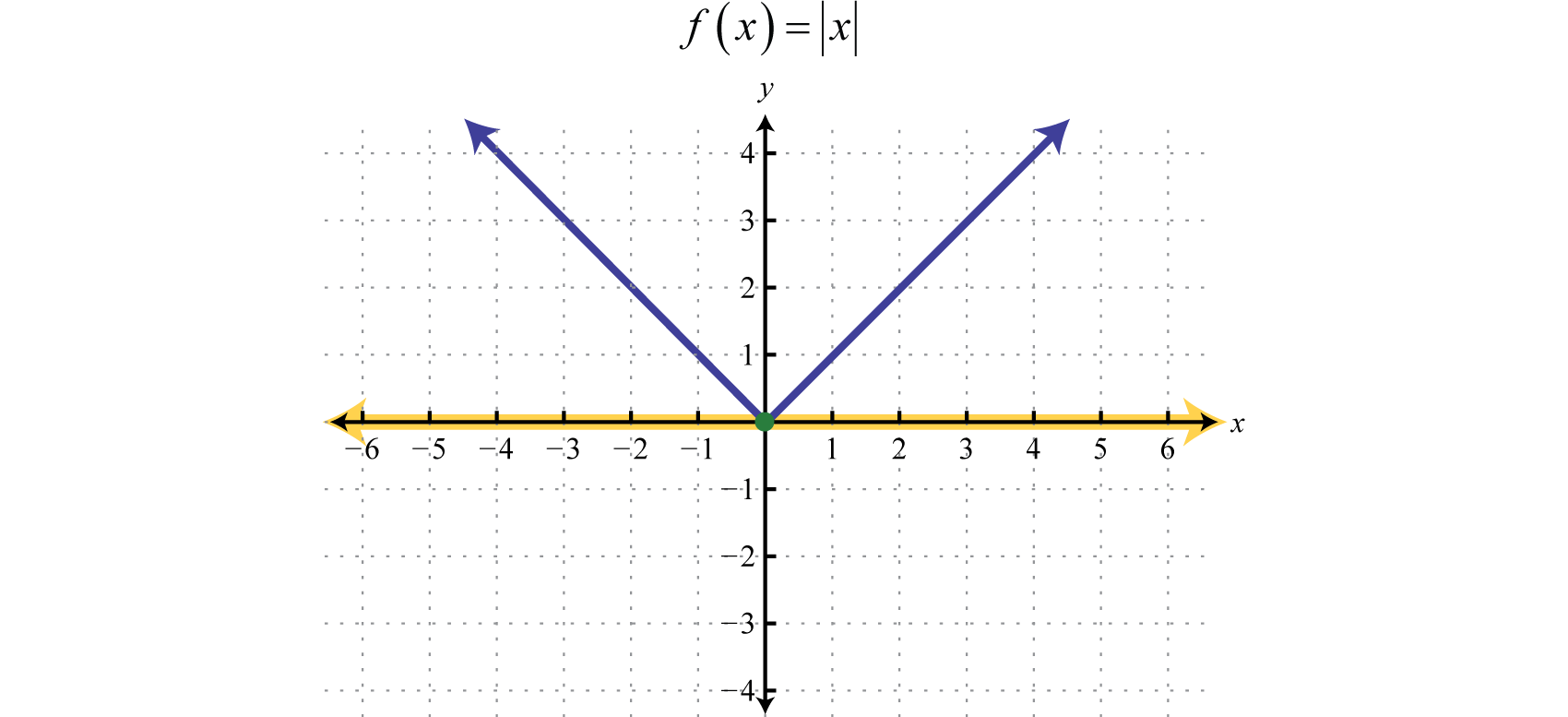
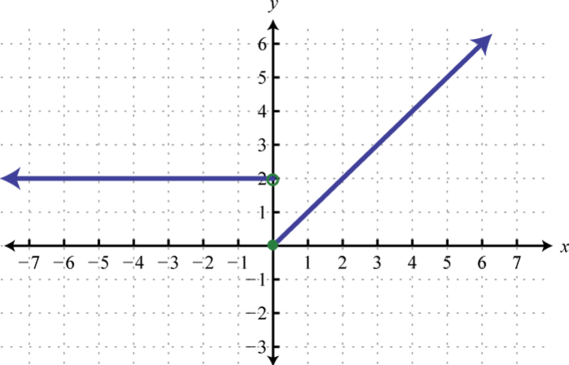
A piecewise functionA function whose definition changes depending on the values in the domain., or split functionA term used when referring to a piecewise function., is a function whose definition changes depending on the value in the domain. For example, we can write the absolute value function as a piecewise function:
In this case, the definition used depends on the sign of the x-value. If the x-value is positive, , then the function is defined by And if the x-value is negative, , then the function is defined by

Following is the graph of the two pieces on the same rectangular coordinate plane:
Example 1
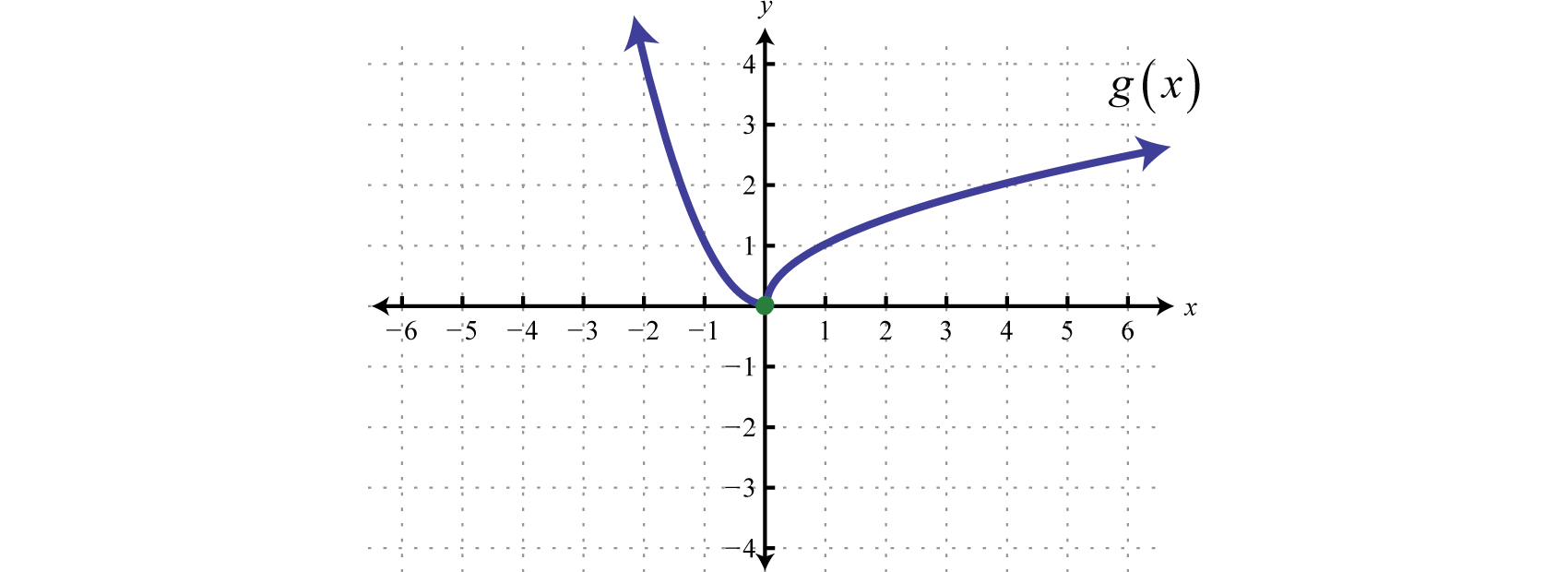
Graph:
Solution:
In this case, we graph the squaring function over negative x-values and the square root function over positive x-values.

Notice the open dot used at the origin for the squaring function and the closed dot used for the square root function. This was determined by the inequality that defines the domain of each piece of the function. The entire function consists of each piece graphed on the same coordinate plane.
Answer:
When evaluating, the value in the domain determines the appropriate definition to use.
Example 2
Given the function , find , , and
Solution:
Use where t is negative, as indicated by
Where t is greater than or equal to zero, use
Answer: , , and
The definition of a function may be different over multiple intervals in the domain.
Example 3
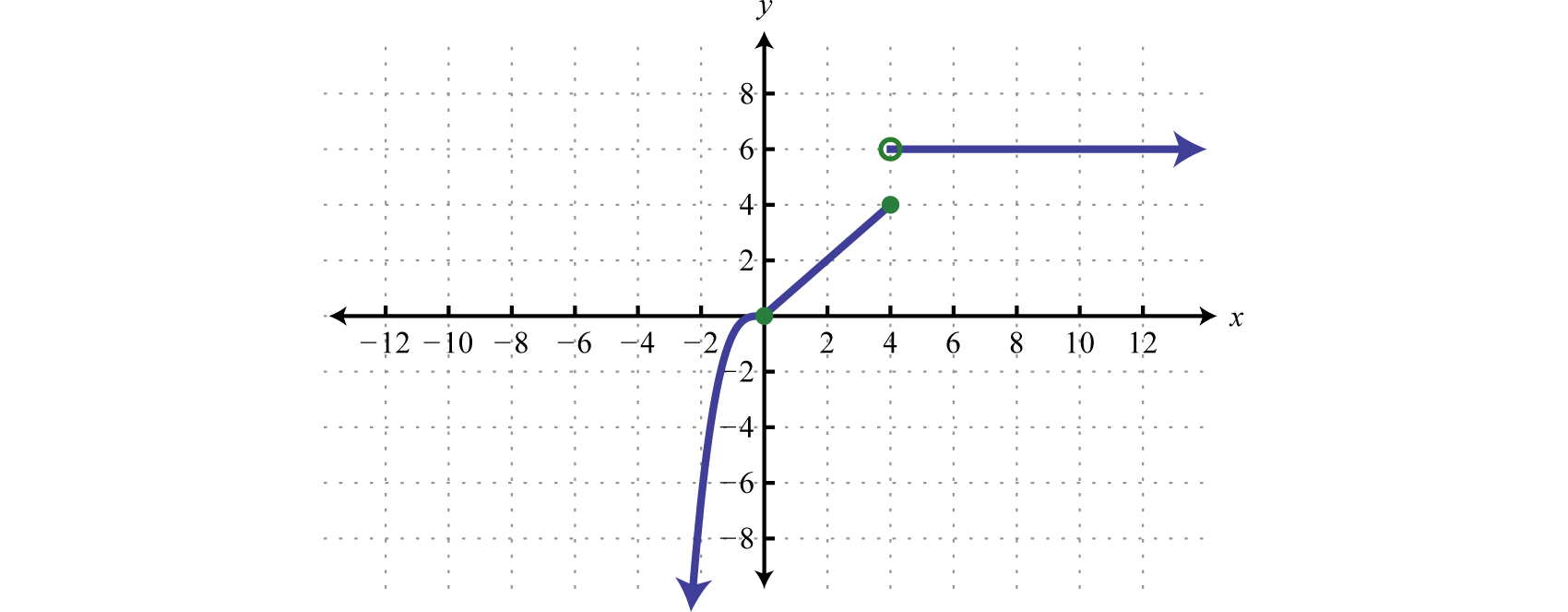
Graph:
Solution:
In this case, graph the cubing function over the interval Graph the identity function over the interval Finally, graph the constant function over the interval And because where , we use an open dot at the point Where , we use and thus is a point on the graph as indicated by a closed dot.
Answer:
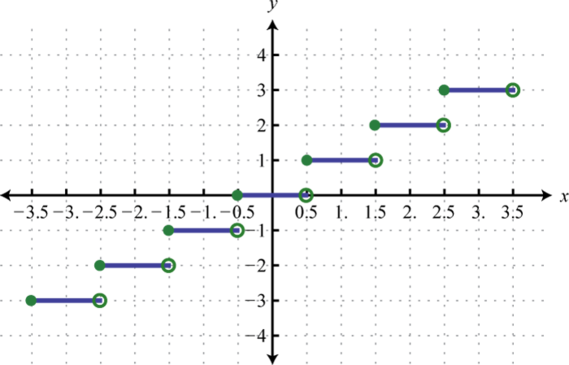
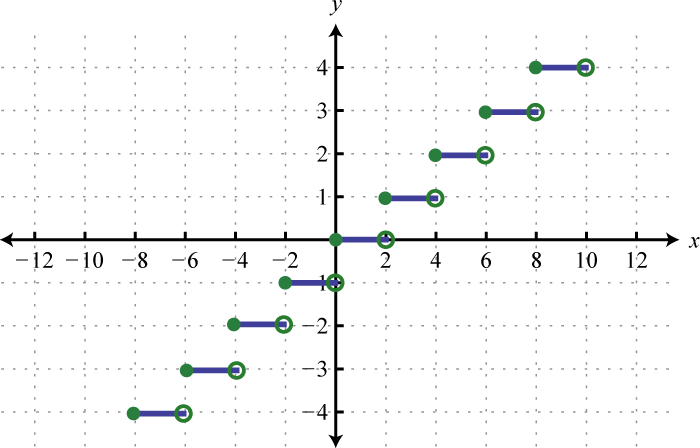
The greatest integer functionThe function that assigns any real number x to the greatest integer less than or equal to x denoted ., denoted , assigns the greatest integer less than or equal to any real number in its domain. For example,
This function associates any real number with the greatest integer less than or equal to it and should not be confused with rounding off.
Example 4
Graph: .
Solution:
If x is any real number, then is the greatest integer less than or equal to x.
Using this, we obtain the following graph.
Answer:
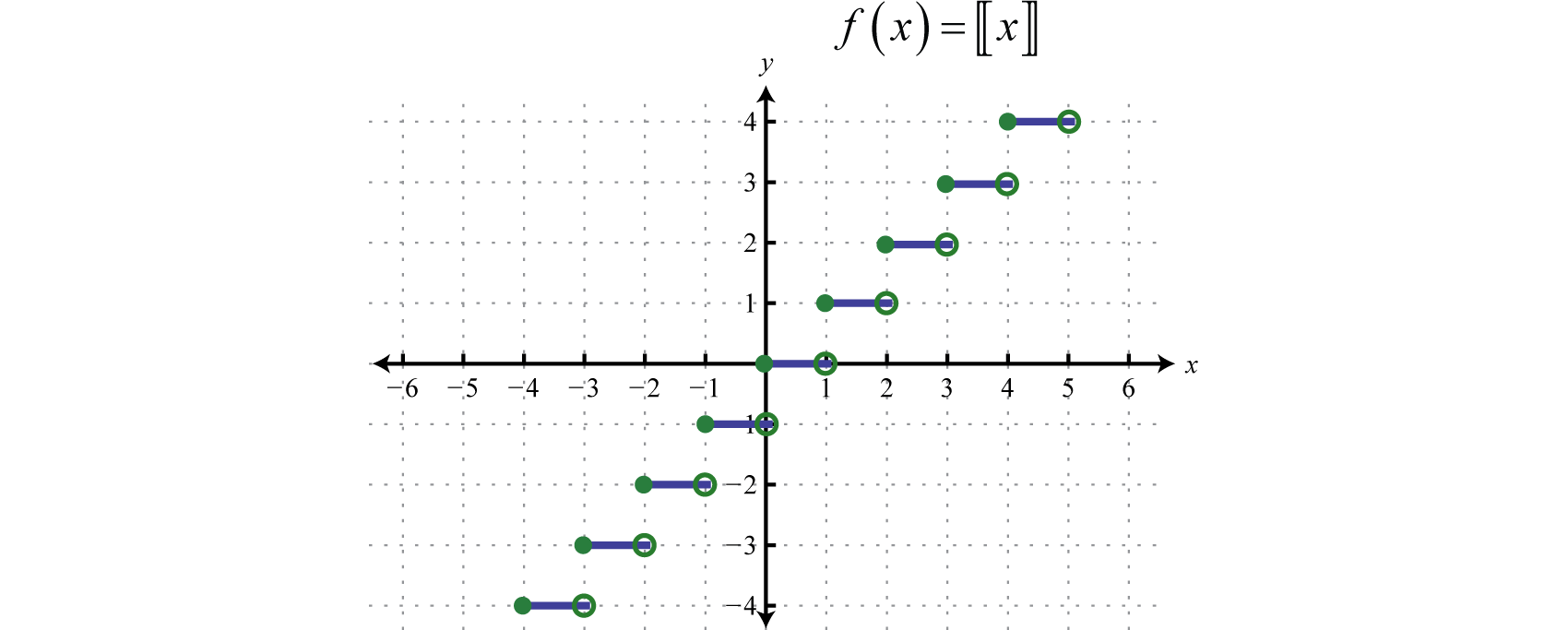
The domain of the greatest integer function consists of all real numbers and the range consists of the set of integers This function is often called the floor functionA term used when referring to the greatest integer function. and has many applications in computer science.
Key Takeaways
- Plot points to determine the general shape of the basic functions. The shape, as well as the domain and range, of each should be memorized.
- The basic polynomial functions are: , , , and
- The basic nonpolynomial functions are: , , and
- A function whose definition changes depending on the value in the domain is called a piecewise function. The value in the domain determines the appropriate definition to use.
Topic Exercises
-
-
-
-
-
-
-
; find , , and
-
; find , , and
-
; find , , and
-
; find , , and
-
; find , , and where
-
; find , , and where
-
; find , , and
-
; find , , and
-
Graph and state its domain and range.
-
Graph and state its domain and range.
-
Find points on the graph of the function defined by with x-values in the set {−8, −1, 0, 1, 8}.
-
Find points on the graph of the function defined by with x-values in the set {−3, −2, 1, 2, 3}. Use a calculator and round off to the nearest tenth.
-
Graph the cube root function defined by by plotting the points found in the previous two exercises.
-
Determine the domain and range of the cube root function.
-
-
-
-
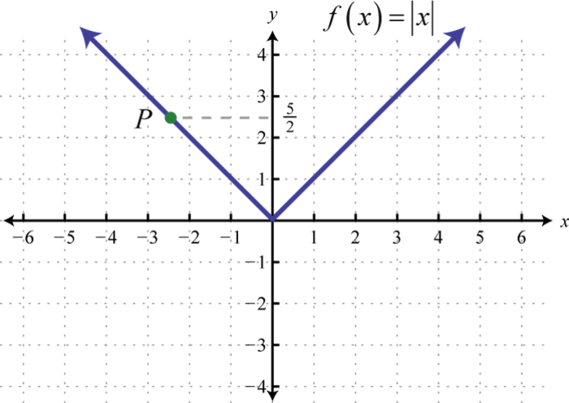
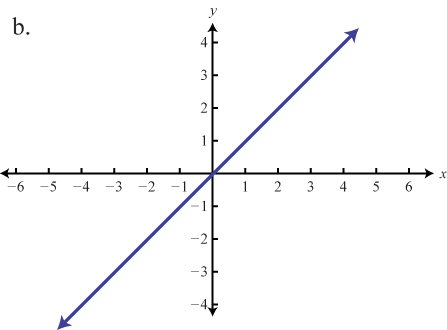
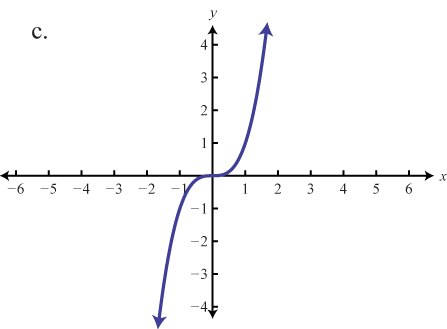
Part A: Basic Functions
Match the graph to the function definition.
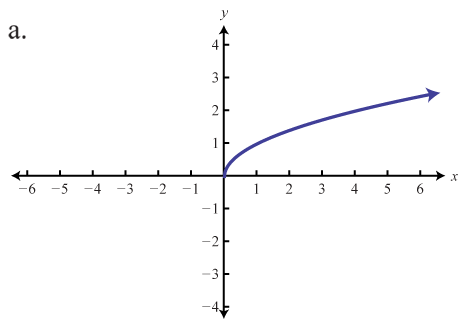
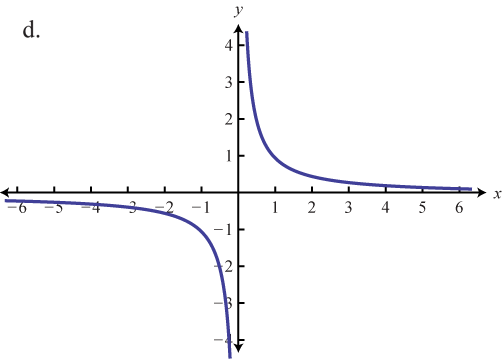
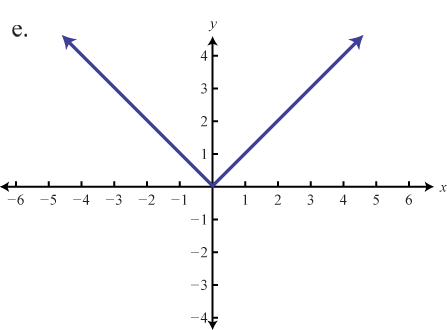
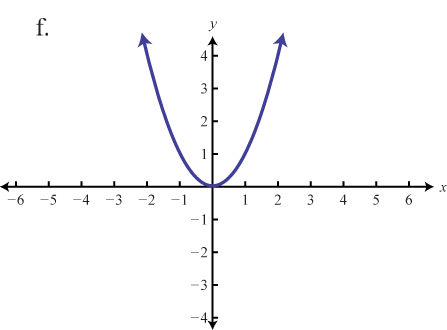
Evaluate.
Cube root function.
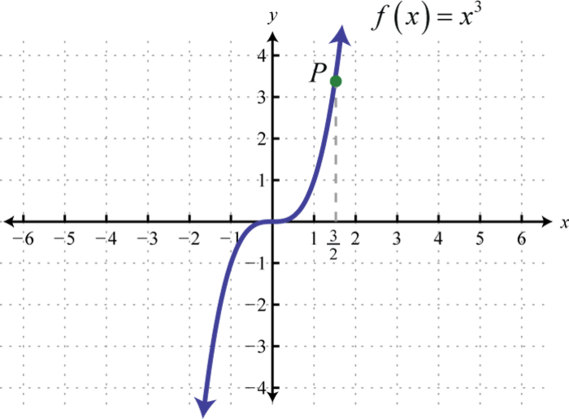
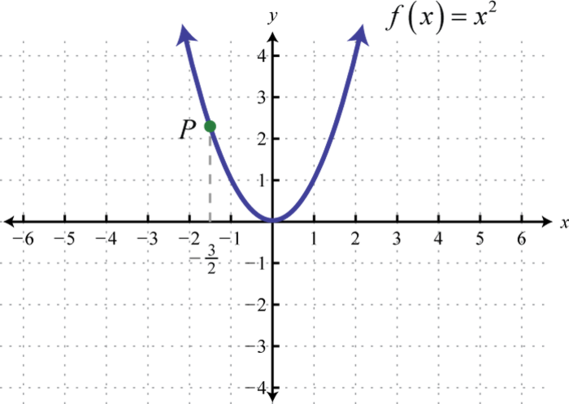
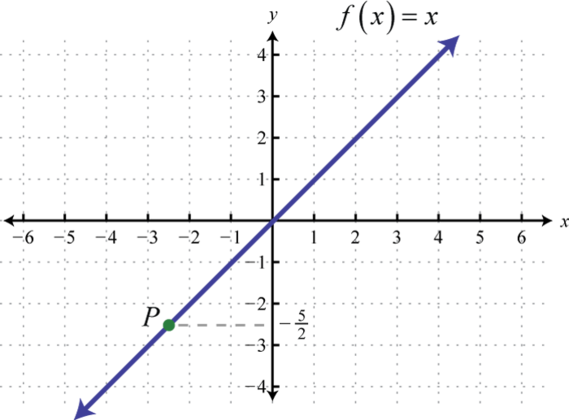
Find the ordered pair that specifies the point P.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Find , , and
-
Find , , and
-
Find , , and
-
Find , , and
-
Find , , and
-
Find , , and
-
Find , , and
-
Find , , and
-
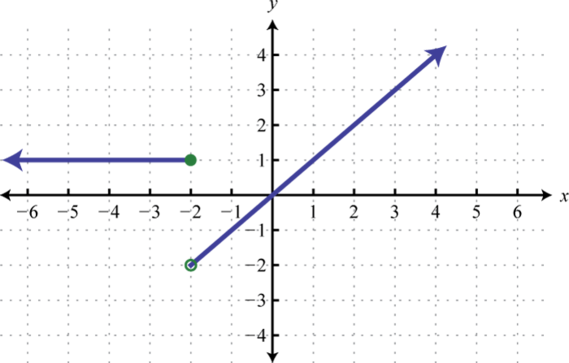
Find , , and
-
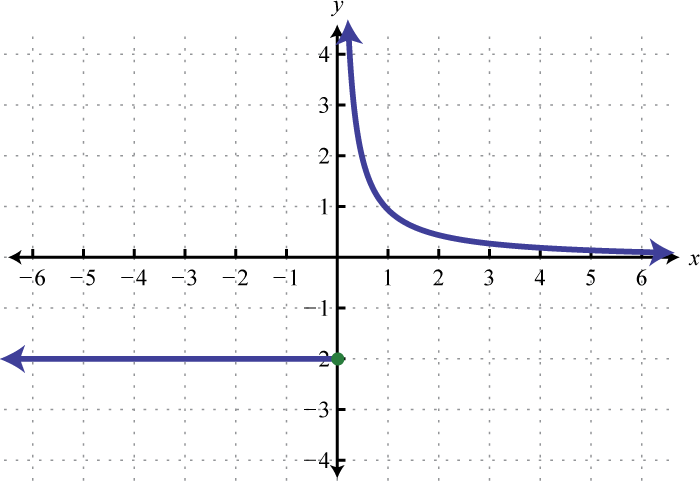
Find , , and
-
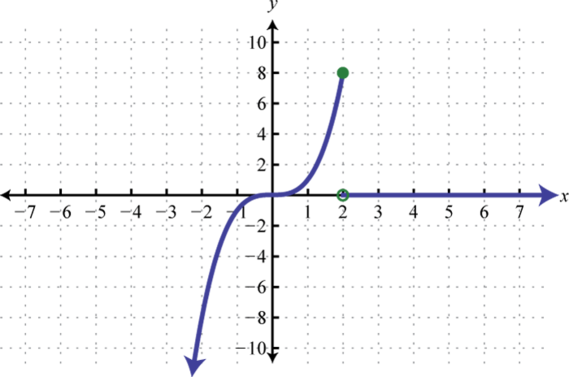
Find , , and
-
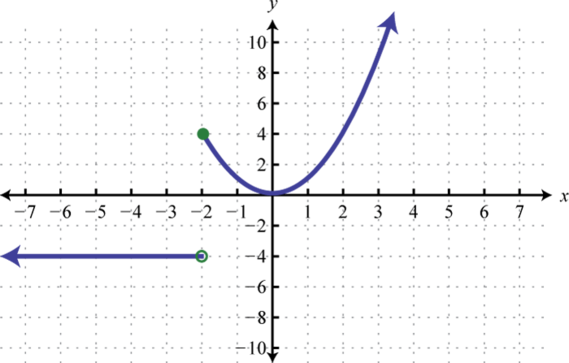
Find , , and
-
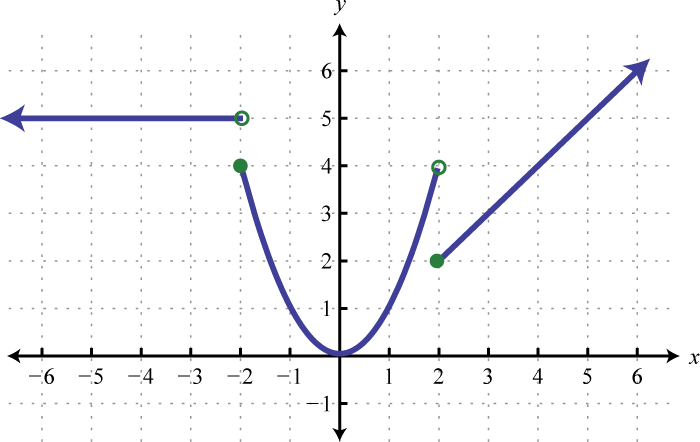
Find , , and
-
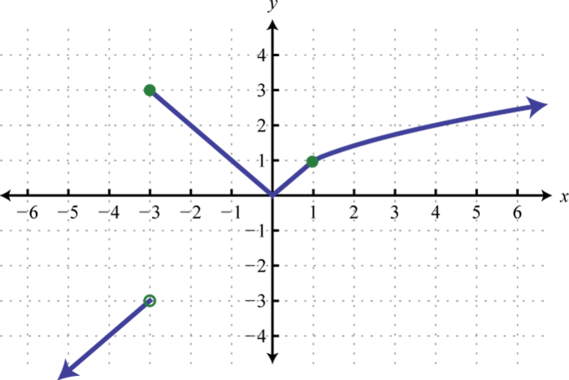
Find , , and
-
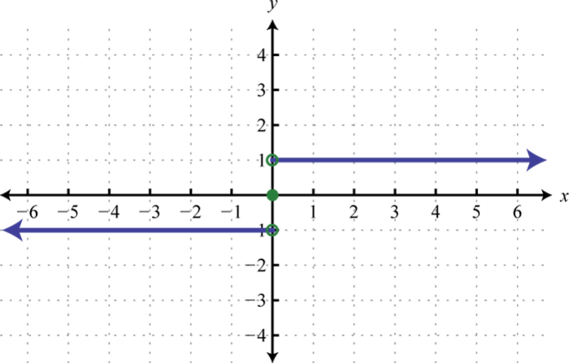
Find , , and
-
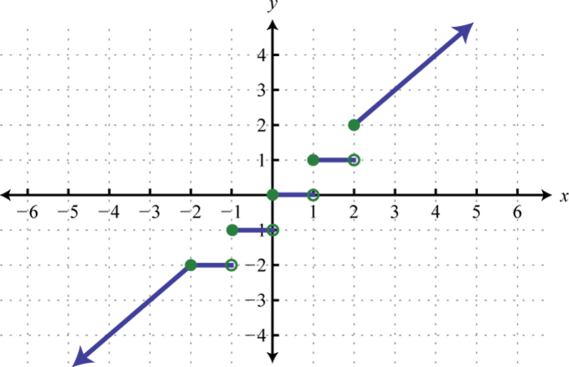
Find , , and
-
The value of an automobile in dollars is given in terms of the number of years since it was purchased new in 1975:

- Determine the value of the automobile in the year 1980.
- In what year is the automobile valued at $9,000?
-
The cost per unit in dollars of custom lamps depends on the number of units produced according to the following graph:
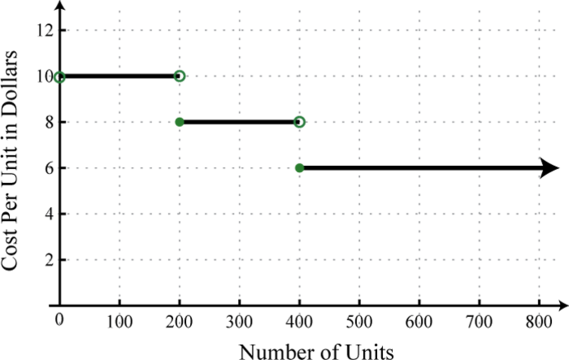
- What is the cost per unit if 250 custom lamps are produced?
- What level of production minimizes the cost per unit?
-
An automobile salesperson earns a commission based on total sales each month x according to the function:
- If the salesperson’s total sales for the month are $35,500, what is her commission according to the function?
- To reach the next level in the commission structure, how much more in sales will she need?
-
A rental boat costs $32 for one hour, and each additional hour or partial hour costs $8. Graph the cost of the rental boat and determine the cost to rent the boat for hours.
Part B: Piecewise Functions
Graph the piecewise functions.
Evaluate.
Evaluate given the graph of f.
-
Explain to a beginning algebra student what an asymptote is.
-
Research and discuss the difference between the floor and ceiling functions. What applications can you find that use these functions?
Part C: Discussion Board
Answers
-
b
-
-
c
-
-
a
-
-
, ,
-
-
, ,
-
-
, ,
-
-
, ,
-
-
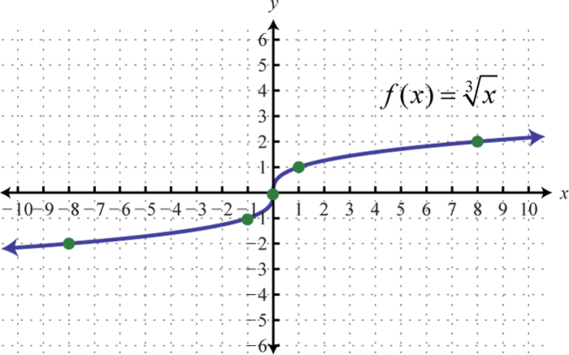
Domain: ; range:
-
-
{(−8,−2), (−1,−1), (0,0), (1,1), (8,2)}
-
-
-
-
-
-
-
-
-
-
-
-
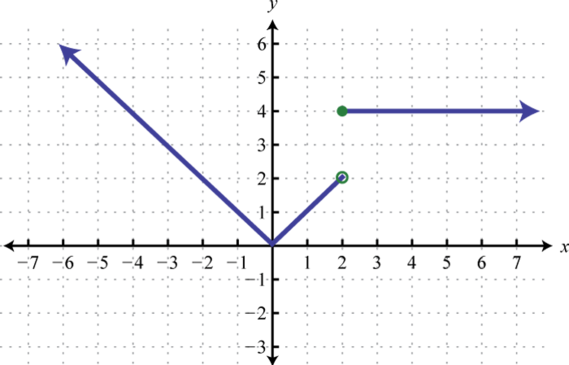
-
-
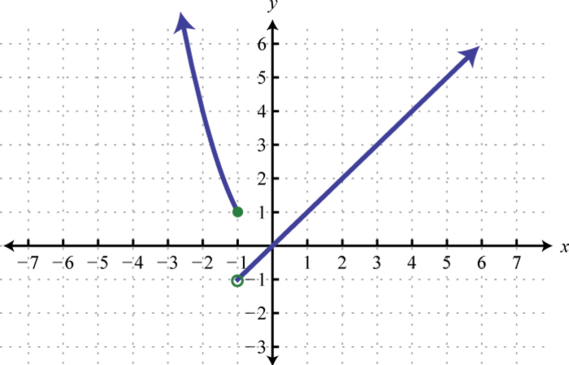
-
-
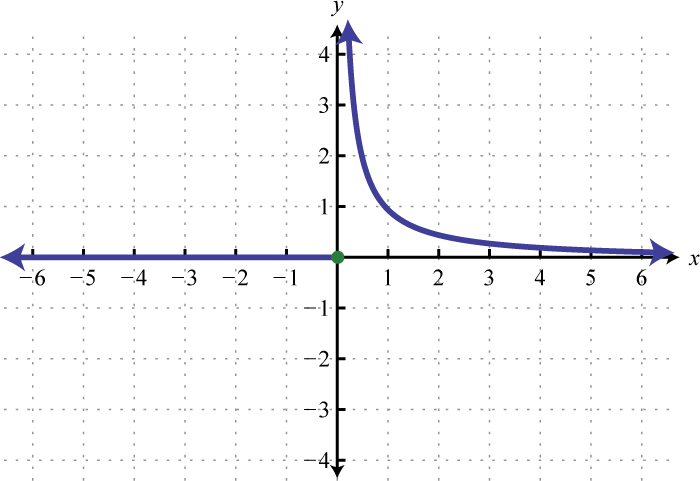
-
-
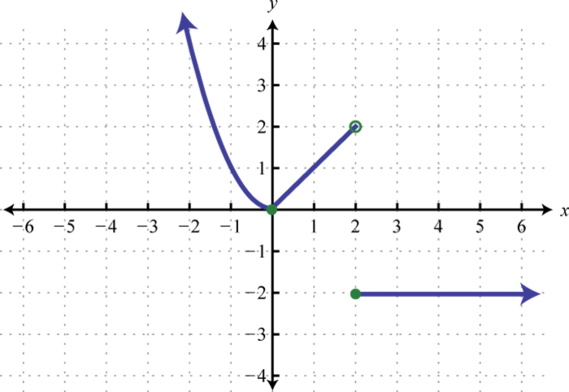
-
-

-
-
-
-
-
-
-
-
, , and
-
-
, , and
-
-
, , and
-
-
, , and
-
-
, , and
-
-
, , and
-
-
, , and
-
-
, , and
-
-
- $3,000;
- 2005
-
-
- $1,775;
- $14,500
-
-
Answer may vary
-