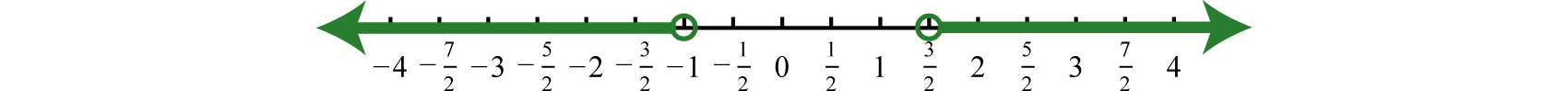This is “Algebra Fundamentals”, chapter 1 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
Chapter 1 Algebra Fundamentals
1.1 Review of Real Numbers and Absolute Value
Learning Objectives
- Review the set of real numbers.
- Review the real number line and notation.
- Define the geometric and algebraic definition of absolute value.
Real Numbers
Algebra is often described as the generalization of arithmetic. The systematic use of variablesLetters used to represent numbers., letters used to represent numbers, allows us to communicate and solve a wide variety of real-world problems. For this reason, we begin by reviewing real numbers and their operations.
A setAny collection of objects. is a collection of objects, typically grouped within braces { }, where each object is called an elementAn object within a set.. When studying mathematics, we focus on special sets of numbers.
The three periods (…) are called an ellipsis and indicate that the numbers continue without bound. A subsetA set consisting of elements that belong to a given set., denoted , is a set consisting of elements that belong to a given set. Notice that the sets of naturalThe set of counting numbers: {1, 2, 3, 4, 5, …}. and whole numbersThe set of natural numbers combined with zero: {0, 1, 2, 3, 4, 5, …}. are both subsets of the set of integers and we can write:
A set with no elements is called the empty setA subset with no elements, denoted Ø or { }. and has its own special notation:
Rational numbersNumbers of the form , where a and b are integers and b is nonzero., denoted , are defined as any number of the form where a and b are integers and b is nonzero. We can describe this set using set notationNotation used to describe a set using mathematical symbols.:
The vertical line | inside the braces reads, “such that” and the symbol indicates set membership and reads, “is an element of.” The notation above in its entirety reads, “the set of all numbers such that a and b are elements of the set of integers and b is not equal to zero.” Decimals that terminate or repeat are rational. For example,
The set of integers is a subset of the set of rational numbers, , because every integer can be expressed as a ratio of the integer and 1. In other words, any integer can be written over 1 and can be considered a rational number. For example,
Irrational numbersNumbers that cannot be written as a ratio of two integers. are defined as any numbers that cannot be written as a ratio of two integers. Nonterminating decimals that do not repeat are irrational. For example,
Finally, the set of real numbersThe set of all rational and irrational numbers., denoted , is defined as the set of all rational numbers combined with the set of all irrational numbers. Therefore, all the numbers defined so far are subsets of the set of real numbers. In summary,

The set of even integersIntegers that are divisible by 2. is the set of all integers that are evenly divisible by 2. We can obtain the set of even integers by multiplying each integer by 2.
The set of odd integersNonzero integers that are not divisible by 2. is the set of all nonzero integers that are not evenly divisible by 2.
A prime numberInteger greater than 1 that is divisible only by 1 and itself. is an integer greater than 1 that is divisible only by 1 and itself. The smallest prime number is 2 and the rest are necessarily odd.
Any integer greater than 1 that is not prime is called a composite numberIntegers greater than 1 that are not prime. and can be uniquely written as a product of primes. When a composite number, such as 42, is written as a product, , we say that is a factorizationAny combination of factors, multiplied together, resulting in the product. of 42 and that 2 and 21 are factorsAny of the numbers that form a product.. Note that factors divide the number evenly. We can continue to write composite factors as products until only a product of primes remains.

Therefore, the prime factorizationThe unique factorization of a natural number written as a product of primes. of 42 is
Example 1
Determine the prime factorization of 210.
Solution:
Begin by writing 210 as a product with 10 as a factor. Then continue factoring until only a product of primes remains.
Since the prime factorization is unique, it does not matter how we choose to initially factor the number; the end result will be the same.
Answer:
A fractionA rational number written as a quotient of two integers: , where is a rational number written as a quotient, or ratio, of two integers a and b where .

The integer above the fraction bar is called the numeratorThe number above the fraction bar. and the integer below is called the denominatorThe number below the fraction bar.. Two equal ratios expressed using different numerators and denominators are called equivalent fractionsTwo equal fractions expressed using different numerators and denominators.. For example,
Consider the following factorizations of 50 and 100:
The numbers 50 and 100 share the factor 25. A shared factor is called a common factorA factor that is shared by more than one real number.. Making use of the fact that , we have
Dividing and replacing this factor with a 1 is called cancellingThe process of dividing out common factors in the numerator and the denominator.. Together, these basic steps for finding equivalent fractions define the process of reducingThe process of finding equivalent fractions by dividing the numerator and the denominator by common factors.. Since factors divide their product evenly, we achieve the same result by dividing both the numerator and denominator by 25 as follows:
Finding equivalent fractions where the numerator and denominator are relatively primeNumbers that have no common factor other than 1., or have no common factor other than 1, is called reducing to lowest termsFinding equivalent fractions where the numerator and the denominator share no common integer factor other than 1.. This can be done by dividing the numerator and denominator by the greatest common factor (GCF).The largest shared factor of any number of integers. The GCF is the largest number that divides a set of numbers evenly. One way to find the GCF of 50 and 100 is to list all the factors of each and identify the largest number that appears in both lists. Remember, each number is also a factor of itself.
Common factors are listed in bold, and we see that the greatest common factor is 50. We use the following notation to indicate the GCF of two numbers: GCF(50, 100) = 50. After determining the GCF, reduce by dividing both the numerator and the denominator as follows:
Example 2
Reduce to lowest terms:
Solution:
A quick way to find the GCF of the numerator and denominator requires us to first write each as a product of primes. The GCF will be the product of all the common prime factors.
In this case, the product of the common prime factors is 36.
We can convert the improper fraction to a mixed number ; however, it is important to note that converting to a mixed number is not part of the reducing process. We consider improper fractions, such as , to be reduced to lowest terms. In algebra it is often preferable to work with improper fractions, although in some applications, mixed numbers are more appropriate.
Answer:
Recall the relationship between multiplication and division:
In this case, the dividendA number to be divided by another number. 12 is evenly divided by the divisorThe number that is divided into the dividend. 6 to obtain the quotientThe result of division. 2. It is true in general that if we multiply the divisor by the quotient we obtain the dividend. Now consider the case where the dividend is zero and the divisor is nonzero:
This demonstrates that zero divided by any nonzero real number must be zero. Now consider a nonzero number divided by zero:
Zero times anything is zero and we conclude that there is no real number such that Thus, the quotient is undefinedA quotient such as is left without meaning and is not assigned an interpretation.. Try it on a calculator, what does it say? For our purposes, we will simply write “undefined.” To summarize, given any real number , then
We are left to consider the case where the dividend and divisor are both zero.
Here, any real number seems to work. For example, and also, Therefore, the quotient is uncertain or indeterminateA quotient such as is a quantity that is uncertain or ambiguous..
In this course, we state that is undefined.
The Number Line and Notation
A real number lineA line that allows us to visually represent real numbers by associating them with points on the line., or simply number line, allows us to visually display real numbers by associating them with unique points on a line. The real number associated with a point is called a coordinateThe real number associated with a point on a number line.. A point on the real number line that is associated with a coordinate is called its graphA point on the number line associated with a coordinate.. To construct a number line, draw a horizontal line with arrows on both ends to indicate that it continues without bound. Next, choose any point to represent the number zero; this point is called the originThe point on the number line that represents zero..
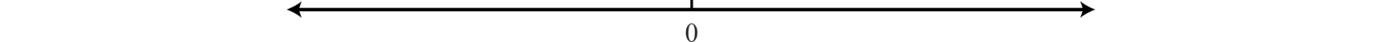
Positive real numbers lie to the right of the origin and negative real numbers lie to the left. The number zero (0) is neither positive nor negative. Typically, each tick represents one unit.
As illustrated below, the scale need not always be one unit. In the first number line, each tick mark represents two units. In the second, each tick mark represents :
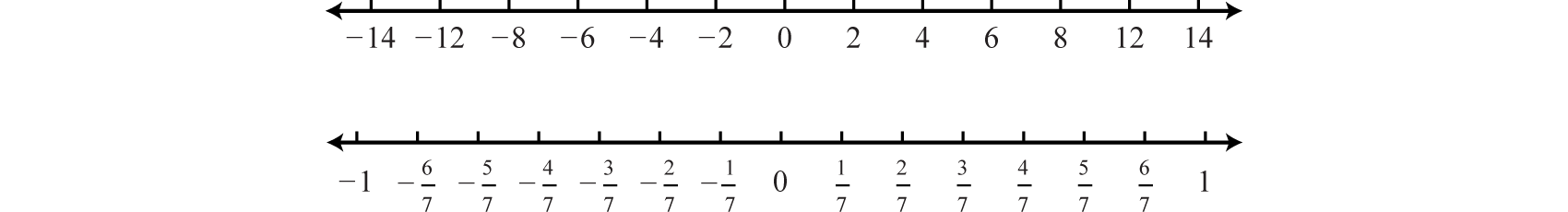
The graph of each real number is shown as a dot at the appropriate point on the number line. A partial graph of the set of integers , follows:

Example 3
Graph the following set of real numbers:
Solution:
Graph the numbers on a number line with a scale where each tick mark represents unit.
Answer:
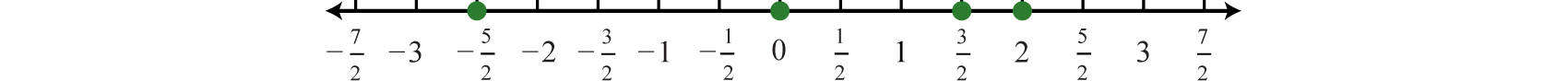
The oppositeReal numbers whose graphs are on opposite sides of the origin with the same distance to the origin. of any real number a is −a. Opposite real numbers are the same distance from the origin on a number line, but their graphs lie on opposite sides of the origin and the numbers have opposite signs.
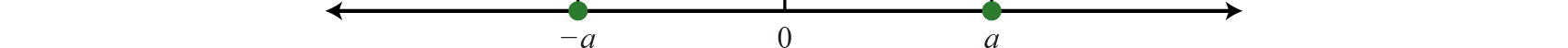
Given the integer −7, the integer the same distance from the origin and with the opposite sign is +7, or just 7.

Therefore, we say that the opposite of −7 is −(−7) = 7. This idea leads to what is often referred to as the double-negative propertyThe opposite of a negative number is positive: −(−a) = a.. For any real number a,
Example 4
Calculate:
Solution:
Here we apply the double-negative within the innermost parentheses first.
Answer:
In general, an odd number of sequential negative signs results in a negative value and an even number of sequential negative signs results in a positive value.
When comparing real numbers on a number line, the larger number will always lie to the right of the smaller one. It is clear that 15 is greater than 5, but it may not be so clear to see that −1 is greater than −5 until we graph each number on a number line.
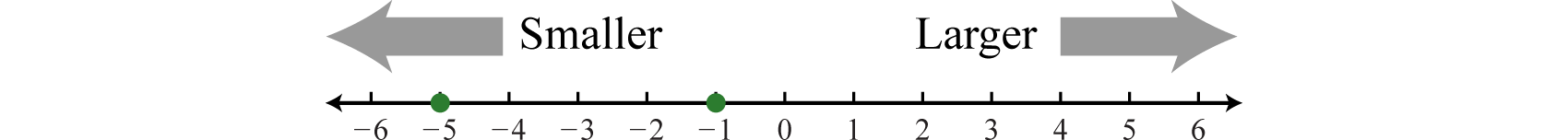
We use symbols to help us efficiently communicate relationships between numbers on the number line.
The relationship between the integersThe set of positive and negative whole numbers combined with zero: {…, −3, −2, −1, 0, 1, 2, 3, …}. in the previous illustration can be expressed two ways as follows:
The symbols < and > are used to denote strict inequalitiesExpress ordering relationships using the symbol < for “less than” and > for “greater than.”, and the symbols and are used to denote inclusive inequalitiesUse the symbol to express quantities that are “less than or equal to” and for quantities that are “greater than or equal to” each other.. In some situations, more than one symbol can be correctly applied. For example, the following two statements are both true:
In addition, the “or equal to” component of an inclusive inequality allows us to correctly write the following:
The logical use of the word “or” requires that only one of the conditions need be true: the “less than” or the “equal to.”
Example 5
Fill in the blank with <, =, or >:
Solution:
Use > because the graph of −2 is to the right of the graph of −12 on a number line. Therefore, −2 > −12, which reads, “negative two is greater than negative twelve.”

Answer: −2 > −12
An algebraic inequalityAlgebraic expressions related with the symbols , <, , and >., such as , is read, “x is greater than or equal to 2.” Here the letter x is a variable, which can represent any real number. However, the statement imposes a condition on the variable. SolutionsValues that can be used in place of the variable to satisfy the given condition. are the values for x that satisfy the condition. This inequality has infinitely many solutions for x, some of which are 2, 3, 4.1, 5, 20, and 20.001. Since it is impossible to list all of the solutions, a system is needed that allows a clear communication of this infinite set. Common ways of expressing solutions to an inequality are by graphing them on a number line, using interval notation, or using set notation.
To express the solution graphically, draw a number line and shade in all the values that are solutions to the inequality. This is called the graph of the solution setSolutions to an algebraic expression expressed on a number line.. Interval and set notation follow:

In this example, there is an inclusive inequality, which means that the lower-bound 2 is included in the solution set. Denote this with a closed dot on the number line and a square bracket in interval notation. The symbol ∞ is read as “infinityThe symbol ∞ indicates the interval is unbounded to the right.” and indicates that the set is unbounded to the right on a number line. If using a standard keyboard, use (inf) as a shortened form to denote infinity. Now compare the notation in the previous example to that of the strict, or noninclusive, inequality that follows:

Strict inequalities imply that solutions may get very close to the boundary point, in this case 3, but not actually include it. Denote this idea with an open dot on the number line and a round parenthesis in interval notation. The symbol −∞ is read as “negative infinityThe symbol −∞ indicates the interval is unbounded to the left.” and indicates that the set is unbounded to the left on a number line. Infinity is a bound to the real numbers, but is not itself a real number: it cannot be included in the solution set and thus is always enclosed with a parenthesis.
Interval notation is textual and is determined after graphing the solution set on a number line. The numbers in interval notation should be written in the same order as they appear on the number line, with smaller numbers in the set appearing first. Set notation, sometimes called set-builder notation, allows us to describe the set using familiar mathematical notation. For example,
Here, describes the type of number. This implies that the variable x represents a real number. The statement is the condition that describes the set using mathematical notation. At this point in our study of algebra, it is assumed that all variables represent real numbers. For this reason, you can omit the “”, and write
Example 6
Graph the solution set and give the interval and set notation equivalents:
Solution:
Use an open dot at −20, because of the strict inequality <, and shade all real numbers to the left.
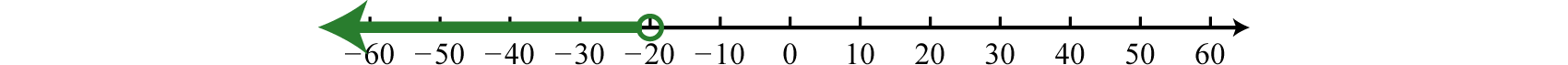
Answer: Interval notation: ; set notation:
A compound inequalityTwo or more inequalities in one statement joined by the word “and” or by the word “or.” is actually two or more inequalities in one statement joined by the word “and” or by the word “or”. Compound inequalities with the logical “or” require that either condition must be satisfied. Therefore, the solution set of this type of compound inequality consists of all the elements of the solution sets of each inequality. When we join these individual solution sets it is called the unionThe set formed by joining the individual solution sets indicated by the logical use of the word “or” and denoted with the symbol , denoted For example,
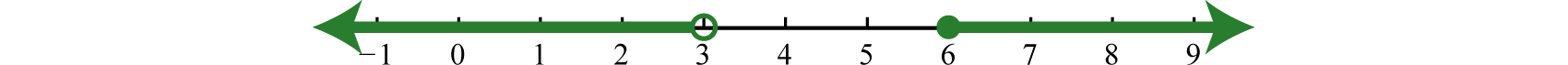
An inequality such as, reads, “negative one is less than or equal to x and x is less than three.” This is actually a compound inequality because it can be decomposed as follows:
The logical “and” requires that both conditions must be true. Both inequalities will be satisfied by all the elements in the intersectionThe set formed by the shared values of the individual solution sets that is indicated by the logical use of the word “and,” denoted with the symbol , denoted , of the solution sets of each.
Example 7
Graph and give the interval notation equivalent:
Solution:
Determine the intersection, or overlap, of the two solution sets to and The solutions to each inequality are sketched above the number line as a means to determine the intersection, which is graphed on the number line below.
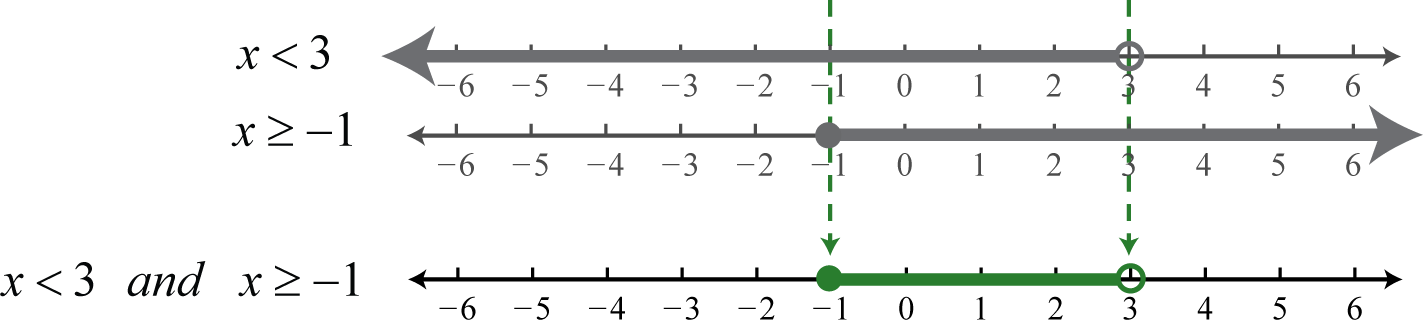
Here, 3 is not a solution because it solves only one of the inequalities. Alternatively, we may interpret as all possible values for x between, or bounded by, −1 and 3 where −1 is included in the solution set.
Answer: Interval notation: ; set notation:
In this text, we will often point out the equivalent notation used to express mathematical quantities electronically using the standard symbols available on a keyboard.
Many calculators, computer algebra systems, and programming languages use the notation presented above, in quotes.
Absolute Value
The absolute valueThe absolute value of a number represents the distance from the graph of the number to zero on a number line. of a real number a, denoted , is defined as the distance between zero (the origin) and the graph of that real number on the number line. Since it is a distance, it is always positive. For example,
Both 4 and −4 are four units from the origin, as illustrated below:
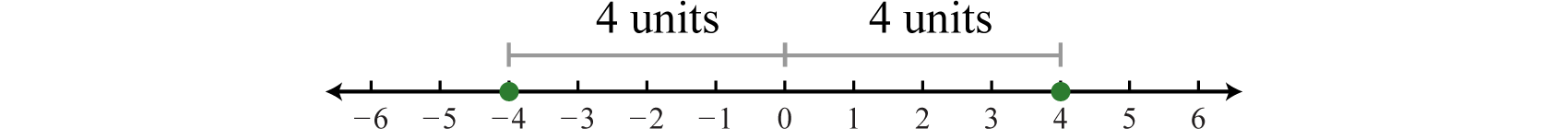
Also, it is worth noting that,
The algebraic definition of the absolute value of a real number a follows:
This is called a piecewise definitionA definition that changes depending on the value of the variable.. The result depends on the quantity a. If a is nonnegative, as indicated by the inequality , then the absolute value will be that number a. If a is negative, as indicated by the inequality , then the absolute value will be the opposite of that number, −a. The results will be the same as the geometric definition. For example, to determine we make note that the value is negative and use the second part of the definition. The absolute value will be the opposite of −4.
At this point, we can determine what real numbers have certain absolute values.
Example 8
Determine the values represented by x:
Solution:
Think of a real number whose distance to the origin is 6 units. There are two solutions: the distance to the right of the origin and the distance to the left of the origin, namely The symbol ± is read “plus or minus” and indicates that there are two answers, one positive and one negative.
Answer:
Example 9
Determine the values represented by x:
Solution:
Here we wish to find a value where the distance to the origin is negative. Since negative distance is not defined, this equation has no solution. Use the empty set Ø to denote this.
Answer: Ø
The absolute value can be expressed textually using the notation abs(a). We often encounter negative absolute values, such as or −abs(3). Notice that the negative sign is in front of the absolute value symbol. In this case, work the absolute value first and then find the opposite of the result.
Try not to confuse this with the double negative property, which states that
Example 10
Simplify:
Solution:
First, find the absolute value of −50 and then apply the double-negative property.
Answer: 50
Key Takeaways
- Algebra is often described as the generalization of arithmetic. The systematic use of variables, used to represent real numbers, allows us to communicate and solve a wide variety of real-world problems. Therefore, it is important to review the subsets of real numbers and their properties.
- The number line allows us to visually display real numbers by associating them with unique points on a line.
- Special notation is used to communicate equality and order relationships between numbers on a number line.
- The absolute value of a real number is defined geometrically as the distance between zero and the graph of that number on a number line. Alternatively, the absolute value of a real number is defined algebraically in a piecewise manner. If a real number a is nonnegative, then the absolute value will be that number a. If a is negative, then the absolute value will be the opposite of that number, −a.
Topic Exercises
-
Every other positive odd number up to 21.
-
Every other positive even number up to 22.
-
The even prime numbers.
-
Rational numbers that are also irrational.
-
The set of negative integers.
-
The set of negative even integers.
-
Three consecutive odd integers starting with 13.
-
Three consecutive even integers starting with 22.
-
195
-
78
-
330
-
273
-
180
-
350
-
-
-
-
-
-
-
-
-
-
Part A: Real Numbers
Use set notation to list the described elements.
Determine the prime factorization of the given composite number.
Reduce to lowest terms.
-
{−5, 5, 10, 15}
-
{−4, −2, 0, 2, 4}
-
-
-
{−5,−4,−3,−1, 1}
-
{−40, −30, −20, 10, 30}
-
−(−10)
-
-
−(−(−12))
-
-
-
-
−10 _____ −15
-
−101 _____ −100
-
−33 _____ 0
-
0 _____ −50
-
−(−(−2)) _____ −(−3)
-
_____
-
_____
-
_____
-
-
-
is irrational.
-
0 is a nonnegative number.
-
Any integer is a rational number.
-
The constant is rational.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
All real numbers less than −15.
-
All real numbers greater than or equal to −7.
-
All real numbers less than 6 and greater than zero.
-
All real numbers less than zero and greater than −5.
-
All real numbers less than or equal to 5 or greater than 10.
-
All real numbers between −2 and 2.
-
-
-
-
-
-
-
-
-
-
-
-
Part B: Number Line and Notation
Graph the following sets of numbers.
Simplify.
Fill in the blank with <, =, or >.
True or False.
Graph the solution set and give the interval notation equivalent.
Write an equivalent inequality.
Determine the inequality given the answers expressed in interval notation.
Part C: Absolute Value
Simplify.
Determine the values represented by a.
-
Research and discuss the origins and evolution of algebra.
-
Research and discuss reasons why algebra is a required subject today.
-
Solution sets to inequalities can be expressed using a graph, interval notation, or set notation. Discuss the merits and drawbacks of each method. Which do you prefer?
-
Research and discuss the Fundamental Theorem of Algebra. Illustrate its idea with an example and share your results.
Part D: Discussion Board
Answers
-
{1, 5, 9, 13, 17, 21}
-
-
{2}
-
-
{…,−3, −2, −1}
-
-
{13, 15, 17}
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
0
-
-

-
-
-
-
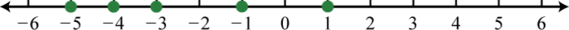
-
-
10
-
-
−12
-
-
-
-
>
-
-
<
-
-
<
-
-
<
-
-
True
-
-
False
-
-
True
-
-
(−∞, −1);
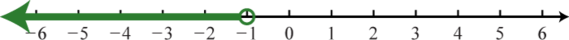
-
-
;

-
-
;

-
-
;

-
-
;

-
-
;

-
-
;
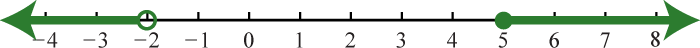
-
-
;

-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
-
-
−4
-
-
-
-
−7
-
-
2
-
-
5
-
-
-
-
-
-
-
-
Answer may vary
-
-
Answer may vary
-
1.2 Operations with Real Numbers
Learning Objectives
- Review the properties of real numbers.
- Simplify expressions involving grouping symbols and exponents.
- Simplify using the correct order of operations.
Working with Real Numbers
In this section, we continue to review the properties of real numbers and their operations. The result of adding real numbers is called the sumThe result of adding. and the result of subtracting is called the differenceThe result of subtracting.. Given any real numbers a, b, and c, we have the following properties of addition:
Additive Identity Property: |
|
Additive Inverse Property: |
|
Associative Property: |
|
Commutative Property: |
Given real numbers a, b and c,
It is important to note that addition is commutative and subtraction is not. In other words, the order in which we add does not matter and will yield the same result. However, this is not true of subtraction.
We use these properties, along with the double-negative property for real numbers, to perform more involved sequential operations. To simplify things, make it a general rule to first replace all sequential operations with either addition or subtraction and then perform each operation in order from left to right.
Example 1
Simplify:
Solution:
Replace the sequential operations and then perform them from left to right.
Answer: −5
Adding or subtracting fractions requires a common denominatorA denominator that is shared by more than one fraction.. Assume the common denominator c is a nonzero integer and we have
Example 2
Simplify:
Solution:
First determine the least common multiple (LCM) of 9, 15, and 45. The least common multiple of all the denominators is called the least common denominatorThe least common multiple of a set of denominators. (LCD). We begin by listing the multiples of each given denominator:
Here we see that the LCM(9, 15, 45) = 45. Multiply the numerator and the denominator of each fraction by values that result in equivalent fractions with the determined common denominator.
Once we have equivalent fractions, with a common denominator, we can perform the operations on the numerators and write the result over the common denominator.
And then reduce if necessary,
Answer:
Finding the LCM using lists of multiples, as described in the previous example, is often very cumbersome. For example, try making a list of multiples for 12 and 81. We can streamline the process of finding the LCM by using prime factors.
The least common multiple is the product of each prime factor raised to the highest power. In this case,
Often we will find the need to translate English sentences involving addition and subtraction to mathematical statements. Below are some common translations.
Example 3
What is 8 subtracted from the sum of 3 and ?
Solution:
We know that subtraction is not commutative; therefore, we must take care to subtract in the correct order. First, add 3 and and then subtract 8 as follows:
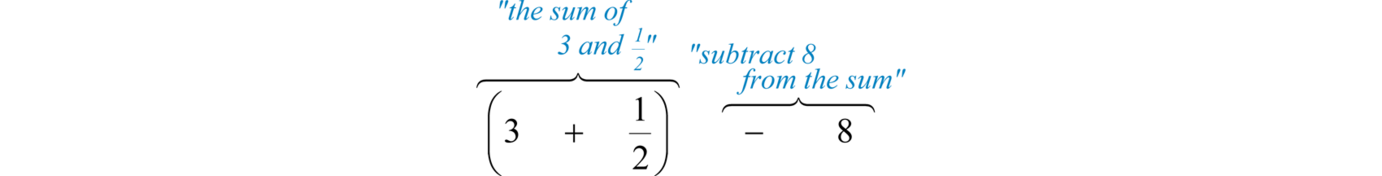
Perform the indicated operations.
Answer:
The result of multiplying real numbers is called the productThe result of multiplying. and the result of dividing is called the quotientThe result of dividing.. Given any real numbers a, b, and c, we have the following properties of multiplication:
Zero Factor Property: |
|
Multiplicative Identity Property: |
|
Associative Property: |
|
Commutative Property: |
Given any real numbers a, b and c,
Given any real numbers a and b,
It is important to note that multiplication is commutative and division is not. In other words, the order in which we multiply does not matter and will yield the same result. However, this is not true of division.
We will use these properties to perform sequential operations involving multiplication and division. Recall that the product of a positive number and a negative number is negative. Also, the product of two negative numbers is positive.
Example 4
Multiply:
Solution:
Multiply two numbers at a time as follows:
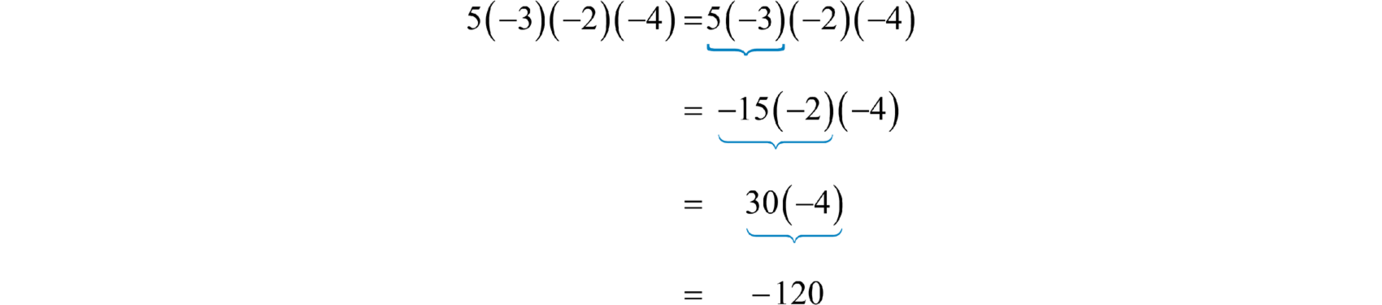
Answer: −120
Because multiplication is commutative, the order in which we multiply does not affect the final answer. However, when sequential operations involve multiplication and division, order does matter; hence we must work the operations from left to right to obtain a correct result.
Example 5
Simplify:
Solution:
Perform the division first; otherwise the result will be incorrect.

Notice that the order in which we multiply and divide does affect the result. Therefore, it is important to perform the operations of multiplication and division as they appear from left to right.
Answer: 25
The product of two fractions is the fraction formed by the product of the numerators and the product of the denominators. In other words, to multiply fractions, multiply the numerators and multiply the denominators:
Example 6
Multiply:
Solution:
Multiply the numerators and multiply the denominators. Reduce by dividing out any common factors.
Answer:
Two real numbers whose product is 1 are called reciprocalsTwo real numbers whose product is 1.. Therefore, and are reciprocals because For example,
Because their product is 1, and are reciprocals. Some other reciprocals are listed below:
This definition is important because dividing fractions requires that you multiply the dividend by the reciprocal of the divisor.
In general,
Example 7
Simplify:
Solution:
Perform the multiplication and division from left to right.
In algebra, it is often preferable to work with improper fractions. In this case, we leave the answer expressed as an improper fraction.
Answer:
Grouping Symbols and Exponents
In a computation where more than one operation is involved, grouping symbols help tell us which operations to perform first. The grouping symbolsParentheses, brackets, braces, and the fraction bar are the common symbols used to group expressions and mathematical operations within a computation. commonly used in algebra are:
All of the above grouping symbols, as well as absolute value, have the same order of precedence. Perform operations inside the innermost grouping symbol or absolute value first.
Example 8
Simplify:
Solution:
Perform the operations within the parentheses first.
Answer:
Example 9
Simplify:
Solution:
The fraction bar groups the numerator and denominator. Hence, they should be simplified separately.
Answer:
If a number is repeated as a factor numerous times, then we can write the product in a more compact form using exponential notationThe compact notation used when a factor a is repeated n times.. For example,
The baseThe factor a in the exponential notation is the factor and the positive integer exponentThe positive integer n in the exponential notation that indicates the number of times the base is used as a factor. indicates the number of times the base is repeated as a factor. In the above example, the base is 5 and the exponent is 4. Exponents are sometimes indicated with the caret (^) symbol found on the keyboard, 5^4 = 5*5*5*5. In general, if a is the base that is repeated as a factor n times, then

When the exponent is 2 we call the result a squareThe result when the exponent of any real number is 2., and when the exponent is 3 we call the result a cubeThe result when the exponent of any real number is 3.. For example,
If the exponent is greater than 3, then the notation is read, “a raised to the nth power.” The base can be any real number,
Notice that the result of a negative base with an even exponent is positive. The result of a negative base with an odd exponent is negative. These facts are often confused when negative numbers are involved. Study the following four examples carefully:
The base is (−3). |
The base is 3. |
|---|---|
The parentheses indicate that the negative number is to be used as the base.
Example 10
Calculate:
Solution:
Here is the base for both problems.
-
Use the base as a factor three times.
-
Use the base as a factor four times.
Answers:
Order of Operations
When several operations are to be applied within a calculation, we must follow a specific order to ensure a single correct result.
- Perform all calculations within the innermost parentheses or grouping symbol first.
- Evaluate all exponents.
- Apply multiplication and division from left to right.
- Perform all remaining addition and subtraction operations last from left to right.
Note that multiplication and division should be worked from left to right. Because of this, it is often reasonable to perform division before multiplication.
Example 11
Simplify:
Solution:
First, evaluate and then perform multiplication and division as they appear from left to right.
Multiplying first would have led to an incorrect result.
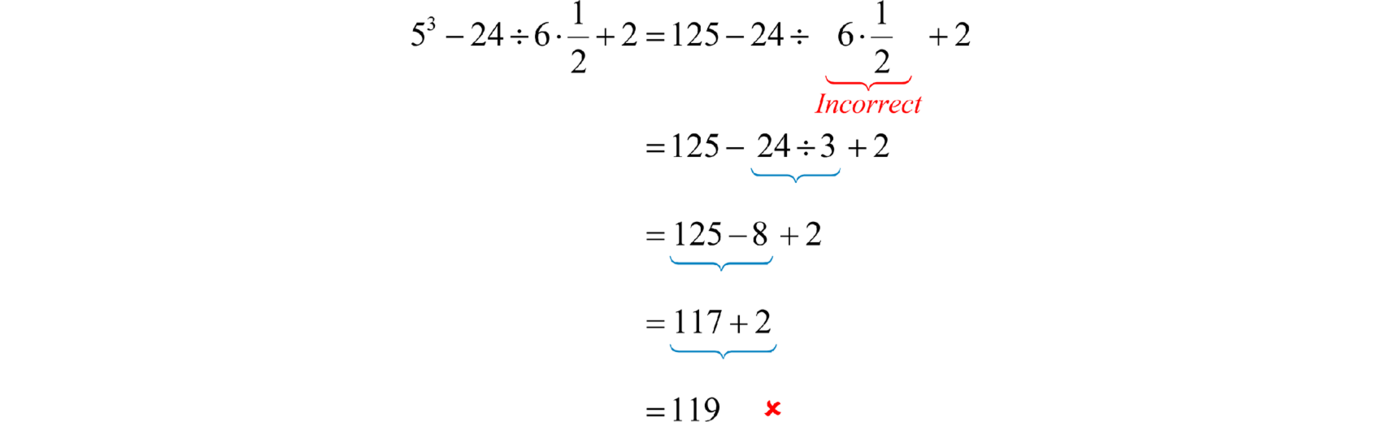
Answer: 125
Example 12
Simplify:
Solution:
Take care to correctly identify the base when squaring.
Answer: 46
We are less likely to make a mistake if we work one operation at a time. Some problems may involve an absolute value, in which case we assign it the same order of precedence as parentheses.
Example 13
Simplify:
Solution:
Begin by performing the operations within the absolute value first.
Subtracting first will lead to incorrect results.

Answer: −18
Key Takeaways
- Addition is commutative and subtraction is not. Furthermore, multiplication is commutative and division is not.
- Adding or subtracting fractions requires a common denominator; multiplying or dividing fractions does not.
- Grouping symbols indicate which operations to perform first. We usually group mathematical operations with parentheses, brackets, braces, and the fraction bar. We also group operations within absolute values. All groupings have the same order of precedence: the operations within the innermost grouping are performed first.
- When using exponential notation , the base a is used as a factor n times. Parentheses indicate that a negative number is to be used as the base. For example, is positive and is negative.
- To ensure a single correct result when applying operations within a calculation, follow the order of operations. First, perform operations in the innermost parentheses or groupings. Next, simplify all exponents. Perform multiplication and division operations from left to right. Finally, perform addition and subtraction operations from left to right.
Topic Exercises
-
-
-
-
-
-
-
-
-
-
-
Subtract 3 from 10.
-
Subtract −2 from 16.
-
Subtract from 4.
-
Subtract from
-
Calculate the sum of −10 and 25.
-
Calculate the sum of −30 and −20.
-
Find the difference of 10 and 5.
-
Find the difference of −17 and −3.
-
10 and 15
-
6 and 22
-
0 and 12
-
−8 and 0
-
−5 and −25
-
−12 and −3
-
-
-
-
−12
-
a where
-
-
where
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Find the product of 12 and 7.
-
Find the product of and 12.
-
Find the quotient of −36 and 12.
-
Find the quotient of and 9.
-
Subtract 10 from the sum of 8 and −5.
-
Subtract −2 from the sum of −5 and −3.
-
Joe earns $18.00 per hour and “time and a half” for every hour he works over 40 hours. What is his pay for 45 hours of work this week?
-
Billy purchased 12 bottles of water at $0.75 per bottle, 5 pounds of assorted candy at $4.50 per pound, and 15 packages of microwave popcorn costing $0.50 each for his party. What was his total bill?
-
James and Mary carpooled home from college for the Thanksgiving holiday. They shared the driving, but Mary drove twice as far as James. If Mary drove for 210 miles, then how many miles was the entire trip?
-
A foot plank is to be cut into 3 pieces of equal length. What will be the length of each piece?
-
A student earned 72, 78, 84, and 90 points on her first four algebra exams. What was her average test score? (Recall that the average is calculated by adding all the values in a set and dividing that result by the number of elements in the set.)
-
The coldest temperature on Earth, −129° F, was recorded in 1983 at Vostok Station, Antarctica. The hottest temperature on Earth, 136° F, was recorded in 1922 at Al’ Aziziyah, Libya. Calculate the temperature range on Earth.
Part A: Working with Real Numbers
Perform the operations. Reduce all fractions to lowest terms.
The formula gives the distance between any two points on a number line. Determine the distance between the given numbers on a number line.
Determine the reciprocal of the following.
Perform the operations.
Part B: Grouping Symbols and Exponents
Perform the operations.
Perform the operations.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Calculate the sum of the squares of the first three consecutive positive odd integers.
-
Calculate the sum of the squares of the first three consecutive positive even integers.
-
What is 6 subtracted from the sum of the squares of 5 and 8?
-
What is 5 subtracted from the sum of the cubes of 2 and 3?
Part C: Order of Operations
Simplify.
-
What is PEMDAS and what is it missing?
-
Does 0 have a reciprocal? Explain.
-
Explain why we need a common denominator in order to add or subtract fractions.
-
Explain why is positive and is negative.
Part D: Discussion Board
Answers
-
40
-
-
−20
-
-
-
-
-
-
-
-
7
-
-
-
-
15
-
-
5
-
-
5 units
-
-
12 units
-
-
20 units
-
-
3
-
-
-
-
-
-
-
-
10
-
-
−4
-
-
-
-
−1
-
-
-
-
-
-
84
-
-
−3
-
-
−7
-
-
$855
-
-
315 miles
-
-
81 points
-
-
−12
-
-
−1
-
-
75
-
-
−3
-
-
0
-
-
144
-
-
−144
-
-
−625
-
-
-
-
-
-
1
-
-
−1
-
-
−100
-
-
20
-
-
−17
-
-
41
-
-
35
-
-
-
-
-
-
-
-
−35
-
-
11
-
-
−36
-
-
150
-
-
-
-
35
-
-
83
-
-
Answer may vary
-
-
Answer may vary
-
1.3 Square and Cube Roots of Real Numbers
Learning Objectives
- Calculate the exact and approximate value of the square root of a real number.
- Calculate the exact and approximate value of the cube root of a real number.
- Simplify the square and cube root of a real number.
- Apply the Pythagorean theorem.
The Definition of Square and Cube Roots
A square rootThat number that when multiplied by itself yields the original number. of a number is a number that when multiplied by itself yields the original number. For example, 4 is a square root of 16, because Since , we can say that −4 is a square root of 16 as well. Every positive real number has two square roots, one positive and one negative. For this reason, we use the radical signThe symbol used to denote a square root. to denote the principal (nonnegative) square rootThe non-negative square root. and a negative sign in front of the radical to denote the negative square root.
Zero is the only real number with exactly one square root.
If the radicandThe number within a radical., the number inside the radical sign, is nonzero and can be factored as the square of another nonzero number, then the square root of the number is apparent. In this case, we have the following property:
It is important to point out that a is required to be nonnegative. Note that because the radical denotes the principal square root. Instead,
This distinction will be carefully considered later in the course.
Example 1
Find the square root:
Solution:
Example 2
Find the negative square root:
Solution:
The radicand may not always be a perfect square. If a positive integer is not a perfect square, then its square root will be irrational. Consider , we can obtain an approximation by bounding it using the perfect squares 4 and 9 as follows:
With this we conclude that is somewhere between 2 and 3. This number is better approximated on most calculators using the square root button,
Next, consider the square root of a negative number. To determine the square root of −9, you must find a number that when squared results in −9,
However, any real number squared always results in a positive number,
The square root of a negative number is currently left undefined. Try calculating on your calculator; what does it say? For now, we will state that is not a real number. The square root of a negative number is defined later in the course.
A cube rootThe number that when multiplied by itself three times yields the original number, denoted by of a number is a number that when multiplied by itself three times yields the original number. Furthermore, we denote a cube root using the symbol , where 3 is called the indexThe positive integer n in the notation that is used to indicate an nth root.. For example,
The product of three equal factors will be positive if the factor is positive, and negative if the factor is negative. For this reason, any real number will have only one real cube root. Hence the technicalities associated with the principal root do not apply. For example,
In general, given any real number a, we have the following property:
When simplifying cube roots, look for factors that are perfect cubes.
Example 3
Find the cube root:
Solution:
Example 4
Find the cube root:
Solution:
It may be the case that the radicand is not a perfect cube. If this is the case, then its cube root will be irrational. For example, is an irrational number, which can be approximated on most calculators using the root button Depending on the calculator, we typically type in the index prior to pushing the button and then the radicand as follows:
Therefore, we have
We will extend these ideas using any integer as an index later in this course. It is important to point out that a square root has index 2; therefore, the following are equivalent:
In other words, if no index is given, it is assumed to be the square root.
Simplifying Square and Cube Roots
It will not always be the case that the radicand is a perfect square. If not, we use the following two properties to simplify the expression. Given real numbers and where ,
Product Rule for Radicals: |
|
Quotient Rule for Radicals: |
A simplified radicalA radical where the radicand does not consist of any factors that can be written as perfect powers of the index. is one where the radicand does not consist of any factors that can be written as perfect powers of the index. Given a square root, the idea is to identify the largest square factor of the radicand and then apply the property shown above. As an example, to simplify , notice that 12 is not a perfect square. However, 12 does have a perfect square factor, Apply the property as follows: The number is a simplified irrational number. You are often asked to find an approximate answer rounded off to a certain decimal place. In that case, use a calculator to find the decimal approximation using either the original problem or the simplified equivalent. As a check, calculate and on a calculator and verify that the results are both approximately 3.46.
Example 5
Simplify:
Solution:
Begin by finding the largest perfect square factor of 135.
Therefore,
Answer:
Example 6
Simplify:
Solution:
We begin by finding the prime factorizations of both 108 and 169. This will enable us to easily determine the largest perfect square factors.
Therefore,
Answer:
Example 7
Simplify:
Solution:
Answer:
A cube root is simplified if it does not contain any factors that can be written as perfect cubes. The idea is to identify the largest cube factor of the radicand and then apply the product or quotient rule for radicals. As an example, to simplify , notice that 80 is not a perfect cube. However, and we can write,
Example 8
Simplify:
Solution:
Begin by finding the largest perfect cube factor of 162.
Therefore,
Answer:
Example 9
Simplify:
Solution:
Answer:
Consider the following two calculations,
Notice that it does not matter if we apply the exponent first or the square root first. This is true for any positive real number. We have the following,
Example 10
Simplify:
Solution:
Apply the fact that if a is nonnegative.
Pythagorean Theorem
A right triangleA triangle with an angle that measures 90°. is a triangle where one of the angles measures 90°. The side opposite the right angle is the longest side, called the hypotenuseThe longest side of a right triangle; it will always be the side opposite the right angle., and the other two sides are called legsThe sides of a right triangle that are not the hypotenuse.. Numerous real-world applications involve this geometric figure. The Pythagorean theoremThe hypotenuse of any right triangle is equal to the square root of the sum of the squares of the lengths of the triangle’s legs. states that given any right triangle with legs measuring a and b units, the square of the measure of the hypotenuse c is equal to the sum of the squares of the measures of the legs, In other words, the hypotenuse of any right triangle is equal to the square root of the sum of the squares of its legs.

Example 11
Calculate the diagonal of a square with sides measuring 5 units.
Solution:
The diagonal of a square will form an isosceles right triangle where the two equal legs measure 5 units each.

We can use the Pythagorean theorem to determine the length of the hypotenuse.
Answer: units
The Pythagorean theorem actually states that having side lengths satisfying the property is a necessary and sufficient condition of right triangles. In other words, if we can show that the sum of the squares of the lengths of the legs of the triangle is equal to the square of the hypotenuse, then it must be a right triangle.
Example 12
Determine whether or not a triangle with legs cm and cm and hypotenuse cm is a right triangle.
Solution:
If the legs satisfy the condition then the Pythagorean theorem guarantees that the triangle is a right triangle.
Answer: Yes, the described triangle is a right triangle.
Key Takeaways
- The square root of a number is a number that when squared results in the original number. The principal square root of a positive real number is the positive square root. The square root of a negative number is currently left undefined.
- When simplifying the square root of a number, look for perfect square factors of the radicand. Apply the product or quotient rule for radicals and then simplify.
- The cube root of a number is a number that when cubed results in the original number. Every real number has only one real cube root.
- When simplifying cube roots, look for perfect cube factors of the radicand. Apply the product or quotient rule for radicals and then simplify.
- The Pythagorean theorem gives us a necessary and sufficient condition of right triangles: if and only if a, b and c represent the lengths of the sides of a right triangle.
Topic Exercises
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Determine the set consisting of the squares of the first twelve positive integers.
-
Determine the set consisting of the cubes of the first twelve positive integers.
Part A: Square and Cube Roots
Simplify.
Use a calculator to approximate to the nearest hundredth.
Part B: Simplifying Square Roots and Cube Roots
Simplify.
-
If the two legs of a right triangle measure 3 units and 4 units, then find the length of the hypotenuse.
-
If the two legs of a right triangle measure 6 units and 8 units, then find the length of the hypotenuse.
-
If the two equal legs of an isosceles right triangle measure 7 units, then find the length of the hypotenuse.
-
If the two equal legs of an isosceles right triangle measure 10 units, then find the length of the hypotenuse.
-
Calculate the diagonal of a square with sides measuring 3 centimeters.
-
Calculate the diagonal of a square with sides measuring 10 centimeters.
-
Calculate the diagonal of a square with sides measuring centimeters.
-
Calculate the diagonal of a square with sides measuring centimeters.
-
Calculate the length of the diagonal of a rectangle with dimensions 4 centimeters by 8 centimeters.
-
Calculate the length of the diagonal of a rectangle with dimensions 8 meters by 10 meters.
-
Calculate the length of the diagonal of a rectangle with dimensions meters by 2 meters.
-
Calculate the length of the diagonal of a rectangle with dimensions meters by meters.
-
To ensure that a newly built gate is square, the measured diagonal must match the distance calculated using the Pythagorean theorem. If the gate measures 4 feet by 4 feet, what must the diagonal measure in inches? (Round off to the nearest tenth of an inch.)
-
If a doorframe measures 3.5 feet by 6.6 feet, what must the diagonal measure to ensure that the frame is a perfect rectangle?
-
, , and
-
, , and
-
, , and
-
, , and
-
, , and
-
, , and
-
, , and
-
, , and
Part C: Pythagorean Theorem
Determine whether or not the given triangle with legs a and b and hypotenuse c is a right triangle or not.
-
What does your calculator say after taking the square root of a negative number? Share your results on the discussion board and explain why it says that.
-
Research and discuss the history of the Pythagorean theorem.
-
Research and discuss the history of the square root.
-
Discuss the importance of the principal square root. Why is it that the same issue does not come up with cube roots? Provide some examples with your explanation.
Part D: Discussion Board
Answers
-
9
-
-
−4
-
-
-
-
-
-
Not a real number.
-
-
0.6
-
-
5
-
-
16
-
-
−20
-
-
4
-
-
−3
-
-
0
-
-
0.4
-
-
−10
-
-
−15
-
-
-
-
-
-
32
-
-
24
-
-
1.73
-
-
4.36
-
-
6.71
-
-
1.44
-
-
3.04
-
-
8.62
-
-
{1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144}
-
-
-
-
-
-
-
-
-
-
-
-
Not a real number.
-
-
-
-
-
-
-
-
-
-
-
-
64
-
-
2
-
-
5 units
-
-
units
-
-
centimeters
-
-
centimeters
-
-
centimeters
-
-
meters
-
-
The diagonal must measure approximately 67.9 inches.
-
-
Not a right triangle.
-
-
Right triangle.
-
-
Right triangle.
-
-
Right triangle.
-
-
Answer may vary
-
-
Answer may vary
-
1.4 Algebraic Expressions and Formulas
Learning Objectives
- Identify the parts of an algebraic expression.
- Apply the distributive property.
- Evaluate algebraic expressions.
- Use formulas that model common applications.
Algebraic Expressions and the Distributive Property
In algebra, letters called variables are used to represent numbers. Combinations of variables and numbers along with mathematical operations form algebraic expressionsCombinations of variables and numbers along with mathematical operations used to generalize specific arithmetic operations., or just expressions. The following are some examples of expressions with one variable, :
TermsComponents of an algebraic expression separated by addition operators. in an algebraic expression are separated by addition operators and factorsComponents of a term separated by multiplication operators. are separated by multiplication operators. The numerical factor of a term is called the coefficientThe numerical factor of a term.. For example, the algebraic expression can be thought of as and has three terms. The first term, , represents the quantity where 1 is the coefficient and x and y are the variables. All of the variable factors with their exponents form the variable part of a termAll the variable factors with their exponents.. If a term is written without a variable factor, then it is called a constant termA term written without a variable factor.. Consider the components of ,
Terms |
Coefficient |
Variable Part |
|---|---|---|
1 |
||
6 |
||
−3 |
−3 |
|
The third term in this expression, −3, is called a constant term because it is written without a variable factor. While a variable represents an unknown quantity and may change, the constant term does not change.
Example 1
List all coefficients and variable parts of each term:
Solution:
We want to think of the third term in this example as
Terms |
Coefficient |
Variable Part |
|---|---|---|
10 |
||
−5 |
||
−1 |
Answer: Coefficients: ; Variable parts:
In our study of algebra, we will encounter a wide variety of algebraic expressions. Typically, expressions use the two most common variables, x and y. However, expressions may use any letter (or symbol) for a variable, even Greek letters, such as alpha () and beta (). Some letters and symbols are reserved for constants, such as and Since there is only a limited number of letters, you will also use subscripts,, to indicate different variables.
The properties of real numbers are important in our study of algebra because a variable is simply a letter that represents a real number. In particular, the distributive propertyGiven any real numbers a, b, and c, or states that if given any real numbers a, b and c, then,
This property is one that we apply often when simplifying algebraic expressions. To demonstrate how it will be used, we simplify in two ways, and observe the same correct result.
Working parenthesis first. |
Using the distributive property. |
|---|---|
Certainly, if the contents of the parentheses can be simplified we should do that first. On the other hand, when the contents of parentheses cannot be simplified any further, we multiply every term within it by the factor outside of it using the distributive property. Applying the distributive property allows us to multiply and remove the parentheses.
Example 2
Simplify:
Solution:
Multiply only the terms grouped within the parentheses for which we are applying the distributive property.

Answer:
Recall that multiplication is commutative and therefore we can write the distributive property in the following manner,
Example 3
Simplify:
Solution:
Multiply all terms within the parenthesis by 3.
Answer:
Terms whose variable parts have the same variables with the same exponents are called like termsConstant terms or terms whose variable parts have the same variables with the same exponents., or similar termsUsed when referring to like terms.. Furthermore, constant terms are considered to be like terms. If an algebraic expression contains like terms, apply the distributive property as follows:
In other words, if the variable parts of terms are exactly the same, then we can add or subtract the coefficients to obtain the coefficient of a single term with the same variable part. This process is called combining like termsAdding or subtracting like terms within an algebraic expression to obtain a single term with the same variable part.. For example,
Notice that the variable factors and their exponents do not change. Combining like terms in this manner, so that the expression contains no other similar terms, is called simplifying the expressionThe process of combining like terms until the expression contains no more similar terms.. Use this idea to simplify algebraic expressions with multiple like terms.
Example 4
Simplify:
Solution:
Identify the like terms and add the corresponding coefficients.
Answer:
Example 5
Simplify:
Solution:
Distribute −2 and then combine like terms.
Answer:
Evaluating Algebraic Expressions
An algebraic expression can be thought of as a generalization of particular arithmetic operations. Performing these operations after substituting given values for variables is called evaluatingThe process of performing the operations of an algebraic expression for given values of the variables.. In algebra, a variable represents an unknown value. However, if the problem specifically assigns a value to a variable, then you can replace that letter with the given number and evaluate using the order of operations.
Example 6
Evaluate:
- where
- where
Solution:
To avoid common errors, it is a best practice to first replace all variables with parentheses, and then replace, or substituteThe act of replacing a variable with an equivalent quantity., the appropriate given value.
a.
b.
Answer:
- 14
Often algebraic expressions will involve more than one variable.
Example 7
Evaluate where and
Solution:
After substituting in the appropriate values, we must take care to simplify using the correct order of operations.
Answer: −2
Example 8
Evaluate where and
Solution:
At this point we have a complex fraction. Simplify the numerator and then multiply by the reciprocal of the denominator.
Answer:
The answer to the previous example can be written as a mixed number, Unless the original problem has mixed numbers in it, or it is an answer to a real-world application, solutions will be expressed as reduced improper fractions.
Example 9
Evaluate where , , and
Solution:
Substitute in the appropriate values and then simplify.
Answer:
Using Formulas
The main difference between algebra and arithmetic is the organized use of variables. This idea leads to reusable formulasA reusable mathematical model using algebraic expressions to describe a common application., which are mathematical models using algebraic expressions to describe common applications. For example, the volume of a right circular cone depends on its radius r and height h and is modeled by the formula:
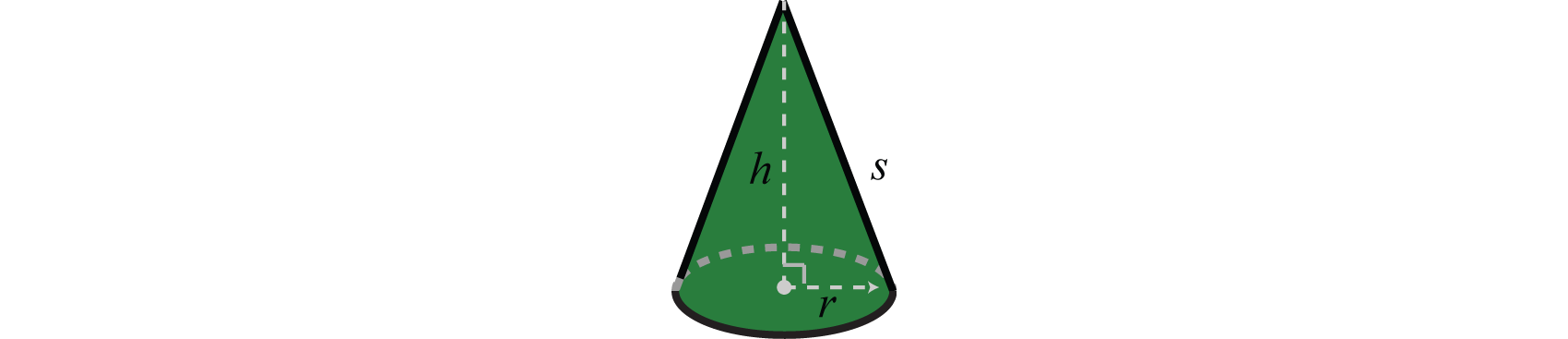
In this equation, variables and constants are used to describe the relationship between volume and the length of the base and height. If the radius of the base measures 3 meters and the height measures 5 meters, then the volume can be calculated using the formula as follows: Using , we can approximate the volume: cubic meters.
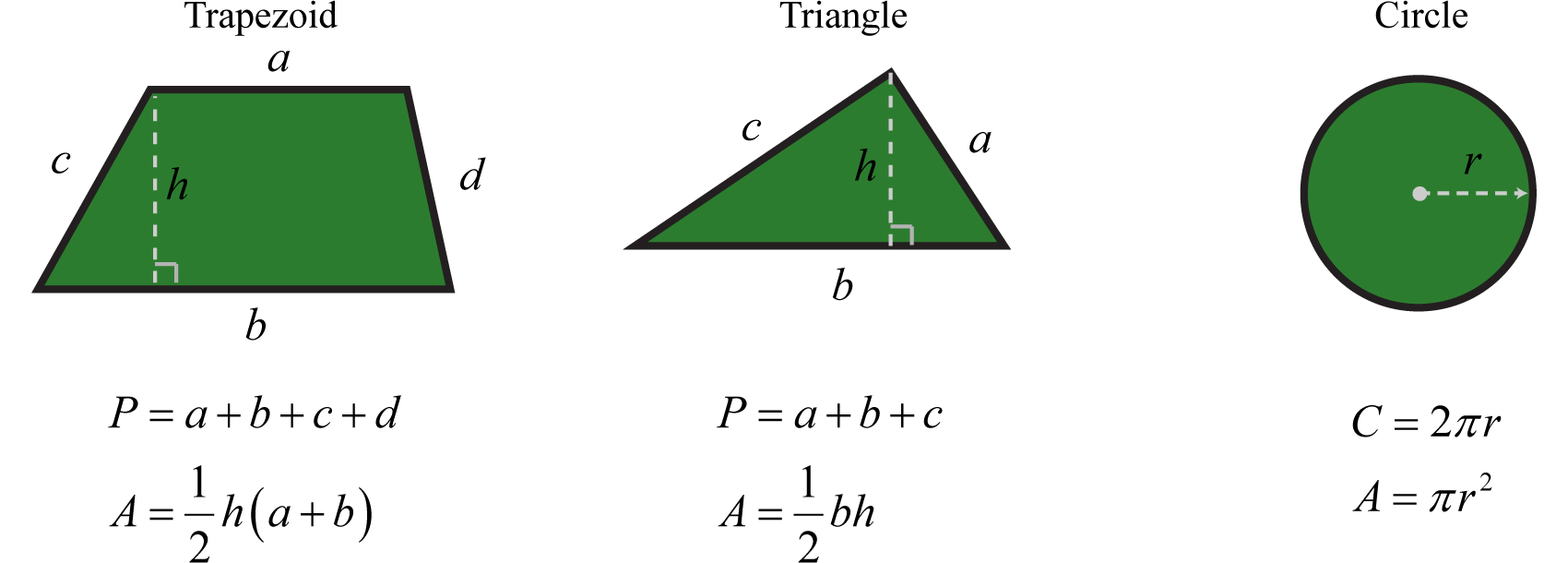
A list of formulas that describe the area and perimeter of common plane figures follows. The letter P represents perimeter and is measured in linear units. The letter A represents area and is measured in square units.
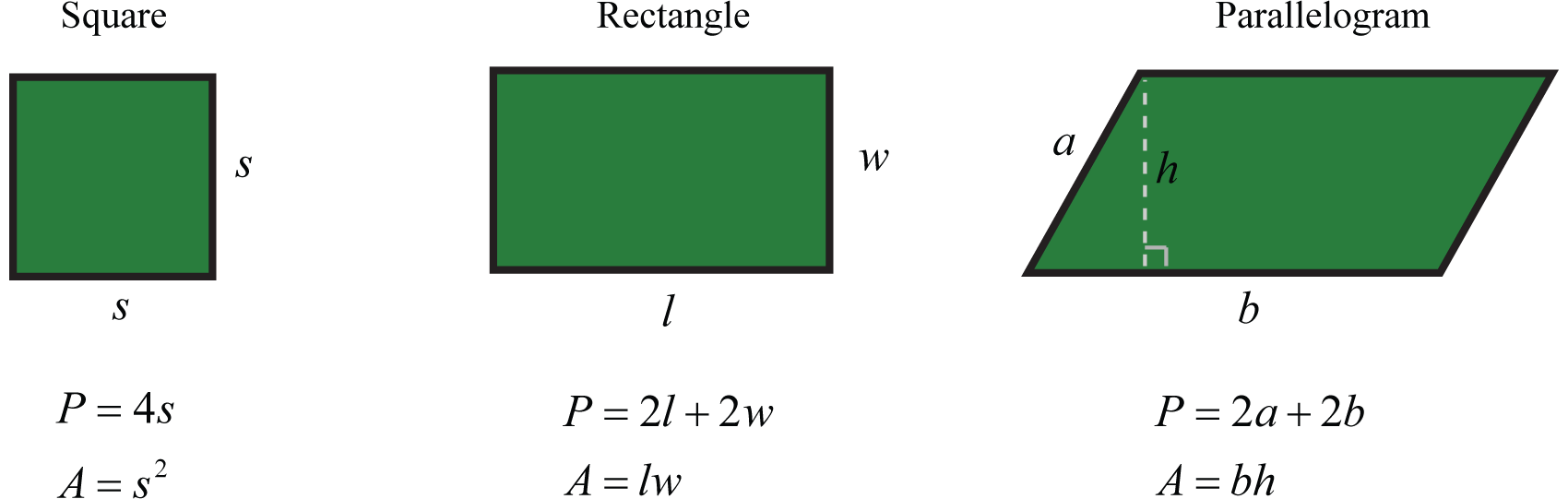
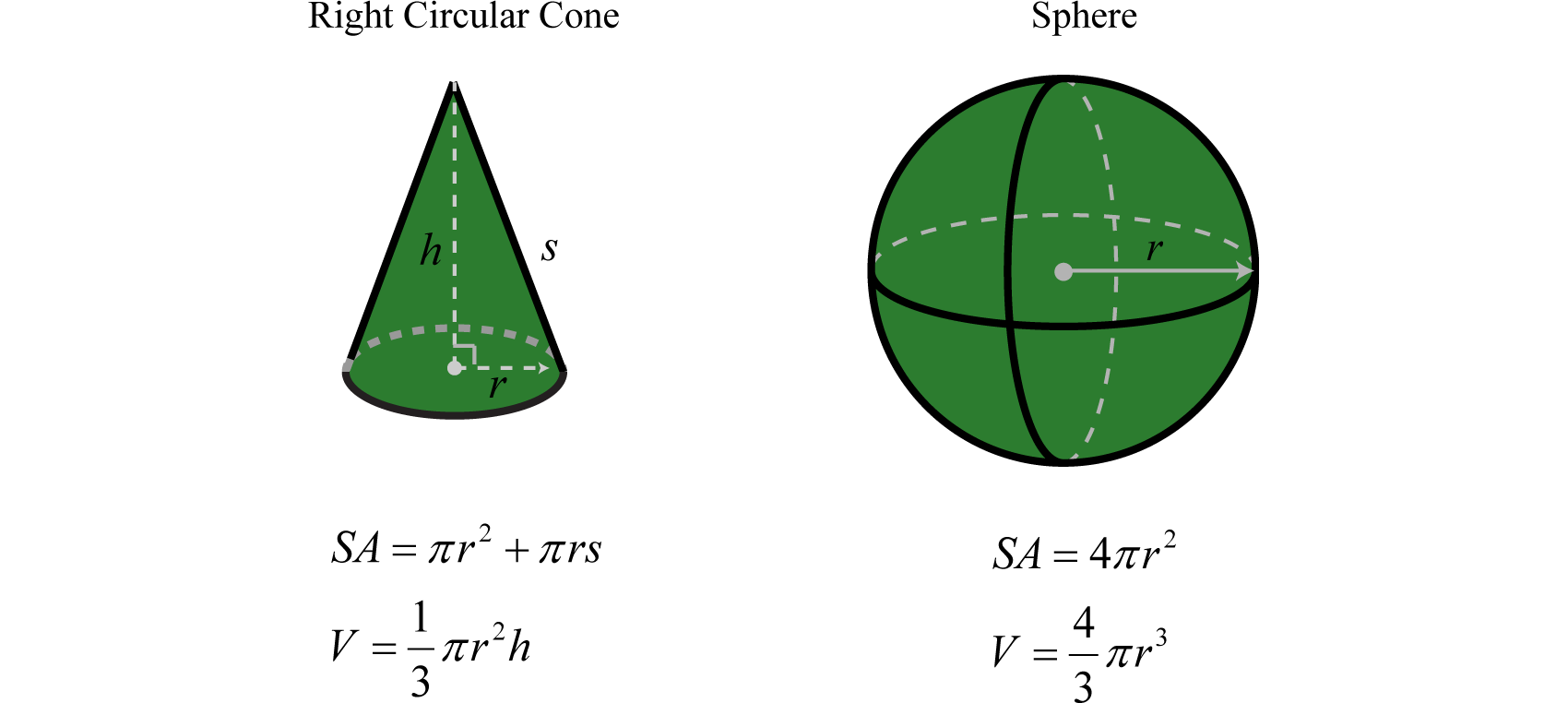
A list of formulas that describe the surface area and volume of common figures follows. Here SA represents surface area and is measured in square units. The letter V represents volume and is measured in cubic units.

Example 10
The diameter of a spherical balloon is 10 inches. Determine the volume rounded off to the nearest hundredth.
Solution:
The formula for the volume of a sphere is
This formula gives the volume in terms of the radius, r. Therefore, divide the diameter by 2 and then substitute into the formula. Here, inches and we have
Answer: The volume of the balloon is approximately 523.60 cubic inches.
Formulas can be found in a multitude of subjects. For example, uniform motionThe distance D after traveling at an average rate r for some time t can be calculated using the formula is modeled by the formula , which expresses distance D, in terms of the average rate, or speed, r and the time traveled at that rate, t. This formula, , is used often and is read, “distance equals rate times time.”
Example 11
Jim’s road trip took hours at an average speed of 66 miles per hour. How far did he travel?
Solution:
Substitute the appropriate values into the formula and then simplify.
Answer: Jim traveled 165 miles.
Simple interestModeled by the formula , where p represents the principal amount invested at an annual interest rate r for t years. is given by the formula , where p represents the principal amount invested at an annual interest rate r for t years.
Example 12
Calculate the simple interest earned on a 2-year investment of $1,250 at an annual interest rate of
Solution:
Convert to a decimal number before using it in the formula.
Use this and the fact that p = $1,250 and t = 2 years to calculate the simple interest.
Answer: The simple interest earned is $93.75.
Key Takeaways
- Think of algebraic expressions as generalizations of common arithmetic operations that are formed by combining numbers, variables, and mathematical operations.
- The distributive property , is used when multiplying grouped algebraic expressions. Applying the distributive property allows us to remove parentheses.
- Combine like terms, or terms whose variable parts have the same variables with the same exponents, by adding or subtracting the coefficients to obtain the coefficient of a single term with the same variable part. Remember that the variable factors and their exponents do not change.
- To avoid common errors when evaluating, it is a best practice to replace all variables with parentheses and then substitute the appropriate values.
- The use of algebraic expressions allows us to create useful and reusable formulas that model common applications.
Topic Exercises
Part A: Algebraic Expressions and the Distributive Property
List all of the coefficients and variable parts of each term.
Multiply.
Combine like terms.
Simplify.
-
where
-
where
-
where
-
where
-
where
-
where
-
where
-
where
-
where
-
where
-
where
-
where
-
where and
-
where and
-
where and
-
where and
-
where and
-
where and
-
where and
-
where and
-
, and
-
, and
-
, and
-
, and
-
, and
-
, and
-
, and
-
, and
Part B: Evaluating Algebraic Expressions
Evaluate.
Evaluate given the following values.
-
95°F
-
86°F
-
32°F
-
−40°F
-
Calculate the perimeter and area of a rectangle with dimensions 12 feet by 5 feet.
-
Calculate the perimeter and area of a rectangle with dimensions 5 meters by 1 meter.
-
Calculate the surface area and volume of a sphere with radius 6 centimeters.
-
The radius of the base of a right circular cylinder measures 4 inches and the height measures 10 inches. Calculate the surface area and volume.
-
Calculate the volume of a sphere with a diameter of 18 centimeters.
-
The diameter of the base of a right circular cone measures 6 inches. If the height is feet, then calculate its volume.
-
Given that the height of a right circular cylinder is equal to the radius of the base, derive a formula for the surface area in terms of the radius of the base.
-
Given that the area of the base of a right circular cylinder is square inches, find the volume if the height is 1 foot.
-
Jose was able to drive from Tucson to Phoenix in 2 hours at an average speed of 58 mph. How far is Phoenix from Tucson?
-
If a bullet train can average 152 mph, then how far can it travel in of an hour?
-
Margaret traveled for hour at an average speed of 68 miles per hour. How far did she travel?
-
The trip from Flagstaff, AZ to the Grand Canyon national park took hours at an average speed of 54 mph. How far is the Grand Canyon national park from Flagstaff?
-
Calculate the simple interest earned on a 3-year investment of $2,500 at an annual interest rate of
-
Calculate the simple interest earned on a 1-year investment of $5,750 at an annual interest rate of
-
What is the simple interest earned on a 5-year investment of $20,000 at an annual interest rate of 6%?
-
What is the simple interest earned on a 1-year investment of $50,000 at an annual interest rate of 4.5%?
-
The time t in seconds an object is in free fall is given by the formula , where s represents the distance in feet the object has fallen. How long does it take an object to fall 32 feet? (Give the exact answer and the approximate answer to the nearest hundredth.)
-
The current I measured in amperes, is given by the formula , where P is the power usage measured in watts, and R is the resistance measured in ohms. If a light bulb uses 60 watts of power and has 240 ohms of resistance, then how many amperes of current are required?
Part C: Using Formulas
Convert the following temperatures to degrees Celsius given , where F represents degrees Fahrenheit.
-
Find and post a useful mathematical model. Demonstrate its use with some values.
-
Research and discuss the history of the variable. What can we use if we run out of letters?
-
Find and post a link to a useful resource describing the Greek alphabet.
-
Given the algebraic expression , explain why we do not subtract 5 and 3 first.
-
Do we need a separate distributive property for more than two terms? For example, Explain.
-
How can we check to see if we have simplified an expression correctly?
Part D: Discussion Board
Answers
-
Coefficients: ; variable parts:
-
-
Coefficients: ; variable parts:
-
-
Coefficients: ; variable parts:
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
7
-
-
35
-
-
-
-
0
-
-
36
-
-
4
-
-
−1
-
-
−96
-
-
3
-
-
−65
-
-
5
-
-
4
-
-
-
-
-
-
35°C
-
-
0°C
-
-
P = 34 feet; A = 60 square feet
-
-
SA = 144π square centimeters; V = 288π cubic centimeters
-
-
cubic centimeters
-
-
-
-
116 miles
-
-
119 miles
-
-
$393.75
-
-
$6,000
-
-
seconds
-
-
Answer may vary
-
-
Answer may vary
-
-
Answer may vary
-
1.5 Rules of Exponents and Scientific Notation
Learning Objectives
- Review the rules of exponents.
- Review the definition of negative exponents and zero as an exponent.
- Work with numbers using scientific notation.
Review of the Rules of Exponents
In this section, we review the rules of exponents. Recall that if a factor is repeated multiple times, then the product can be written in exponential form The positive integer exponent n indicates the number of times the base x is repeated as a factor.

Consider the product of and ,

Expanding the expression using the definition produces multiple factors of the base which is quite cumbersome, particularly when n is large. For this reason, we have useful rules to help us simplify expressions with exponents. In this example, notice that we could obtain the same result by adding the exponents.
In general, this describes the product rule for exponents; the product of two expressions with the same base can be simplified by adding the exponents.. In other words, when multiplying two expressions with the same base we add the exponents. Compare this to raising a factor involving an exponent to a power, such as

Here we have 4 factors of , which is equivalent to multiplying the exponents.
This describes the power rule for exponents; a power raised to a power can be simplified by multiplying the exponents.. Now we consider raising grouped products to a power. For example,
After expanding, we are left with four factors of the product This is equivalent to raising each of the original grouped factors to the fourth power and applying the power rule.
In general, this describes the use of the power rule for a product as well as the power rule for exponents. In summary, the rules of exponents streamline the process of working with algebraic expressions and will be used extensively as we move through our study of algebra. Given any positive integers m and n where we have
Product rule for exponents: |
|
Quotient rule for exponents: |
|
Power rule for exponents: |
|
Power rule for a product: |
|
Power rule for a quotient: |
; if a product is raised to a power, then apply that power to each factor in the product.
; if a quotient is raised to a power, then apply that power to the numerator and the denominator.
These rules allow us to efficiently perform operations with exponents.
Example 1
Simplify:
Solution:
Answer:
In the previous example, notice that we did not multiply the base 10 times itself. When applying the product rule, add the exponents and leave the base unchanged.
Example 2
Simplify:
Solution:
Recall that the variable x is assumed to have an exponent of one,
Answer:
The base could in fact be any algebraic expression.
Example 3
Simplify:
Solution:
Treat the expression as the base.
Answer:
The commutative property of multiplication allows us to use the product rule for exponents to simplify factors of an algebraic expression.
Example 4
Simplify:
Solution:
Multiply the coefficients and add the exponents of variable factors with the same base.
Answer:
Division involves the quotient rule for exponents.
Example 5
Simplify:
Solution:
Answer:
The power rule for a quotient allows us to apply that exponent to the numerator and denominator. This rule requires that the denominator is nonzero and so we will make this assumption for the remainder of the section.
Example 6
Simplify:
Solution:
First apply the power rule for a quotient and then the power rule for a product.
Answer:
Using the quotient rule for exponents, we can define what it means to have zero as an exponent. Consider the following calculation:
Twenty-five divided by twenty-five is clearly equal to one, and when the quotient rule for exponents is applied, we see that a zero exponent results. In general, given any nonzero real number x and integer n,
This leads us to the definition of zero as an exponent; any nonzero base raised to the 0 power is defined to be 1.,
It is important to note that is indeterminate. If the base is negative, then the result is still positive one. In other words, any nonzero base raised to the zero power is defined to be equal to one. In the following examples assume all variables are nonzero.
Example 7
Simplify:
Solution:
-
Any nonzero quantity raised to the zero power is equal to 1.
-
In the example, , the base is x, not −2x.
Noting that we can write,
In general, given any nonzero real number x and integer n,
This leads us to the definition of negative exponents, given any integer n, where x is nonzero.:
An expression is completely simplified if it does not contain any negative exponents.
Example 8
Simplify:
Solution:
Rewrite the entire quantity in the denominator with an exponent of 2 and then simplify further.
Answer:
Sometimes negative exponents appear in the denominator.
Example 9
Simplify:
Solution:
Answer:
The previous example suggests a property of quotients with negative exponents, given any integers m and n, where and . Given any integers m and n where and , then
This leads us to the property
In other words, negative exponents in the numerator can be written as positive exponents in the denominator and negative exponents in the denominator can be written as positive exponents in the numerator.
Example 10
Simplify:
Solution:
Take care with the coefficient −5, recognize that this is the base and that the exponent is actually positive one: Hence, the rules of negative exponents do not apply to this coefficient; leave it in the numerator.
Answer:
In summary, given integers m and n where we have
Zero exponent: |
|
Negative exponent: |
|
Quotients with negative exponents: |
Furthermore, all of the rules of exponents defined so far extend to any integer exponents. We will expand the scope of these properties to include any real number exponents later in the course.
Scientific Notation
Real numbers expressed using scientific notationReal numbers expressed the form , where n is an integer and have the form, where n is an integer and This form is particularly useful when the numbers are very large or very small. For example,
It is cumbersome to write all the zeros in both of these cases. Scientific notation is an alternative, compact representation of these numbers. The factor indicates the power of ten to multiply the coefficient by to convert back to decimal form:

This is equivalent to moving the decimal in the coefficient fifteen places to the right.
A negative exponent indicates that the number is very small:

This is equivalent to moving the decimal in the coefficient eleven places to the left.
Converting a decimal number to scientific notation involves moving the decimal as well. Consider all of the equivalent forms of with factors of 10 that follow:
While all of these are equal, is the only form expressed in correct scientific notation. This is because the coefficient 5.63 is between 1 and 10 as required by the definition. Notice that we can convert back to decimal form, as a check, by moving the decimal three places to the left.
; the quotient of two expressions with the same base can be simplified by subtracting the exponents.
Example 11
Write using scientific notation.
Solution:
Here we count twelve decimal places to the left of the decimal point to obtain the number 1.075.
Answer:
Example 12
Write using scientific notation.
Solution:
Here we count six decimal places to the right to obtain 3.045.
Answer:
Often we will need to perform operations when using numbers in scientific notation. All the rules of exponents developed so far also apply to numbers in scientific notation.
Example 13
Multiply:
Solution:
Use the fact that multiplication is commutative, and apply the product rule for exponents.
Answer:
Example 14
Divide:
Solution:
Answer:
Example 15
The speed of light is approximately miles per hour. Express this speed in miles per second.
Solution:
A unit analysis indicates that we must divide the number by 3,600.
Answer: The speed of light is approximately miles per second.
Example 16
The Sun moves around the center of the galaxy in a nearly circular orbit. The distance from the center of our galaxy to the Sun is approximately 26,000 light-years. What is the circumference of the orbit of the Sun around the galaxy in meters?
Solution:
One light-year measures meters. Therefore, multiply this by 26,000 or to find the length of 26,000 light years in meters.
The radius r of this very large circle is approximately meters. Use the formula to calculate the circumference of the orbit.
Answer: The circumference of the Sun’s orbit is approximately meters.
Key Takeaways
- When multiplying two quantities with the same base, add exponents:
- When dividing two quantities with the same base, subtract exponents:
- When raising powers to powers, multiply exponents:
- When a grouped quantity involving multiplication and division is raised to a power, apply that power to all of the factors in the numerator and the denominator: and
- Any nonzero quantity raised to the 0 power is defined to be equal to 1:
- Expressions with negative exponents in the numerator can be rewritten as expressions with positive exponents in the denominator:
- Expressions with negative exponents in the denominator can be rewritten as expressions with positive exponents in the numerator:
- Take care to distinguish negative coefficients from negative exponents.
- Scientific notation is particularly useful when working with numbers that are very large or very small.
Topic Exercises
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
How much was the phone worth new?
-
How much will the phone be worth in 1 year?
-
How much will the phone be worth in 3 years?
-
How much will the phone be worth in 10 years?
-
How much will the phone be worth in 100 years?
-
According to the formula, will the phone ever be worthless? Explain.
-
The height of a particular right circular cone is equal to the square of the radius of the base, Find a formula for the volume in terms of r.
-
A sphere has a radius Find the volume in terms of x.
Part A: Rules of Exponents
Simplify. (Assume all variables represent nonzero numbers.)
The value in dollars of a new mobile phone can be estimated by using the formula , where t is the number of years after purchase.
-
-
-
-
-
7,050,000
-
430,000,000,000
-
0.00005001
-
0.000000231
-
-
-
-
-
-
-
-
-
-
-
-
-
The population density of Earth refers to the number of people per square mile of land area. If the total land area on Earth is square miles and the population in 2007 was estimated to be people, then calculate the population density of Earth at that time.
-
In 2008 the population of New York City was estimated to be 8.364 million people. The total land area is 305 square miles. Calculate the population density of New York City.
-
The mass of Earth is kilograms and the mass of the Moon is kilograms. By what factor is the mass of Earth greater than the mass of the Moon?
-
The mass of the Sun is kilograms and the mass of Earth is kilograms. By what factor is the mass of the Sun greater than the mass of Earth? Express your answer in scientific notation.
-
The radius of the Sun is miles and the average distance from Earth to the Moon is miles. By what factor is the radius of the Sun larger than the average distance from Earth to the Moon?
-
One light year, meters, is the distance that light travels in a vacuum in one year. If the distance from our Sun to the nearest star, Proxima Centauri, is estimated to be meters, then calculate the number of years it would take light to travel that distance.
-
It is estimated that there are about 1 million ants per person on the planet. If the world population was estimated to be 6.67 billion people in 2007, then estimate the world ant population at that time.
-
The radius of the earth is meters and the radius of the sun is meters. By what factor is the radius of the Sun larger than the radius of the Earth?
-
A gigabyte is bytes and a megabyte is bytes. If the average song in the MP3 format consumes about 4.5 megabytes of storage, then how many songs will fit on a 4-gigabyte memory card?
-
Water weighs approximately 18 grams per mole. If one mole is about molecules, then approximate the weight of each molecule of water.
Part B: Scientific Notation
Convert to a decimal number.
Rewrite using scientific notation.
Perform the operations.
-
Use numbers to show that
-
Why is indeterminate?
-
Explain to a beginning algebra student why
-
René Descartes (1637) established the usage of exponential form: , , and so on. Before this, how were exponents denoted?
Part C: Discussion Board
Answers
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
−5
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
$210
-
-
$30
-
-
$1.04
-
-
-
-
520,000,000
-
-
0.00000102
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
About 116 people per square mile
-
-
81.2
-
-
1.807
-
-
ants
-
-
Approximately 889 songs
-
-
Answer may vary
-
-
Answer may vary
-
1.6 Polynomials and Their Operations
Learning Objectives
- Identify a polynomial and determine its degree.
- Add and subtract polynomials.
- Multiply and divide polynomials.
Definitions
A polynomialAn algebraic expression consisting of terms with real number coefficients and variables with whole number exponents. is a special algebraic expression with terms that consist of real number coefficients and variable factors with whole number exponents. Some examples of polynomials follow:
The degree of a termThe exponent of the variable. If there is more than one variable in the term, the degree of the term is the sum their exponents. in a polynomial is defined to be the exponent of the variable, or if there is more than one variable in the term, the degree is the sum of their exponents. Recall that ; any constant term can be written as a product of and itself. Hence the degree of a constant term is 0.
Term |
Degree |
|---|---|
, since |
|
1, since |
The degree of a polynomialThe largest degree of all of its terms. is the largest degree of all of its terms.
Polynomial |
Degree |
|---|---|
, because has degree 4. |
|
1, because |
Of particular interest are polynomials with one variableA polynomial where each term has the form , where is any real number and n is any whole number., where each term is of the form Here is any real number and n is any whole number. Such polynomials have the standard form:
Typically, we arrange terms of polynomials in descending order based on the degree of each term. The leading coefficientThe coefficient of the term with the largest degree. is the coefficient of the variable with the highest power, in this case,
Example 1
Write in standard form:
Solution:
Since terms are defined to be separated by addition, we write the following:
In this form, we can see that the subtraction in the original corresponds to negative coefficients. Because addition is commutative, we can write the terms in descending order based on the degree as follows:
Answer:
We classify polynomials by the number of terms and the degree:
Expression |
Classification |
Degree |
|---|---|---|
Monomial (one term) |
7 |
|
Binomial (two terms) |
6 |
|
Trinomial (three terms) |
2 |
|
Polynomial (many terms) |
3 |
We can further classify polynomials with one variable by their degree:
Polynomial |
Name |
|---|---|
5 |
Constant (degree 0) |
Linear (degree 1) |
|
Quadratic (degree 2) |
|
Cubic (degree 3) |
|
Fourth-degree polynomial |
In this text, we call any polynomial of degree an nth-degree polynomial. In other words, if the degree is 4, we call the polynomial a fourth-degree polynomial. If the degree is 5, we call it a fifth-degree polynomial, and so on.
Example 2
State whether the following polynomial is linear or quadratic and give the leading coefficient:
Solution:
The highest power is 2; therefore, it is a quadratic polynomial. Rewriting in standard form we have
Here and thus the leading coefficient is −1.
Answer: Quadratic; leading coefficient: −1
Adding and Subtracting Polynomials
We begin by simplifying algebraic expressions that look like or Here, the coefficients are actually implied to be +1 and −1 respectively and therefore the distributive property applies. Multiply each term within the parentheses by these factors as follows:
Use this idea as a means to eliminate parentheses when adding and subtracting polynomials.
Example 3
Add:
Solution:
The property allows us to eliminate the parentheses, after which we can then combine like terms.
Answer:
Example 4
Add:
Solution:
Remember that the variable parts have to be exactly the same before we can add the coefficients.
Answer:
When subtracting polynomials, the parentheses become very important.
Example 5
Subtract:
Solution:
The property allows us to remove the parentheses after subtracting each term.
Answer:
Subtracting a quantity is equivalent to multiplying it by −1.
Example 6
Subtract:
Solution:
Distribute the −1, remove the parentheses, and then combine like terms. Multiplying the terms of a polynomial by −1 changes all the signs.

Answer:
Multiplying Polynomials
Use the product rule for exponents, , to multiply a monomial times a polynomial. In other words, when multiplying two expressions with the same base, add the exponents. To find the product of monomials, multiply the coefficients and add the exponents of variable factors with the same base. For example,
To multiply a polynomial by a monomial, apply the distributive property, and then simplify each term.
Example 7
Multiply:
Solution:
Apply the distributive property and then simplify.

Answer:
To summarize, multiplying a polynomial by a monomial involves the distributive property and the product rule for exponents. Multiply all of the terms of the polynomial by the monomial. For each term, multiply the coefficients and add exponents of variables where the bases are the same.
In the same manner that we used the distributive property to distribute a monomial, we use it to distribute a binomial. Here we apply the distributive property multiple times to produce the final result. This same result is obtained in one step if we apply the distributive property to a and b separately as follows:
This is often called the FOIL method. Multiply the first, outer, inner, and then last terms.
Example 8
Multiply:
Solution:
Distribute 6x and −1 and then combine like terms.
Answer:
Consider the following two calculations:
This leads us to two formulas that describe perfect square trinomialsThe trinomials obtained by squaring the binomials and :
We can use these formulas to quickly square a binomial.
Example 9
Multiply:
Solution:
Here and Apply the formula:
Answer:
This process should become routine enough to be performed mentally. Our third special product follows: This product is called difference of squaresThe special product obtained by multiplying conjugate binomials :
The binomials and are called conjugate binomialsThe binomials and . When multiplying conjugate binomials the middle terms are opposites and their sum is zero; the product is itself a binomial.
Example 10
Multiply:
Solution:
Answer:
Example 11
Multiply:
Solution:
Here we perform one product at a time.

Answer:
Dividing Polynomials
Use the quotient rule for exponents, , to divide a polynomial by a monomial. In other words, when dividing two expressions with the same base, subtract the exponents. In this section, we will assume that all variables in the denominator are nonzero.
Example 12
Divide:
Solution:
Divide the coefficients and apply the quotient rule by subtracting the exponents of the like bases.
Answer:
When dividing a polynomial by a monomial, we may treat the monomial as a common denominator and break up the fraction using the following property: Applying this property will result in terms that can be treated as quotients of monomials.
Example 13
Divide:
Solution:
Break up the fraction by dividing each term in the numerator by the monomial in the denominator, and then simplify each term.
Answer:
We can check our division by multiplying our answer, the quotient, by the monomial in the denominator, the divisor, to see if we obtain the original numerator, the dividend.
or |
or |
The same technique outlined for dividing by a monomial does not work for polynomials with two or more terms in the denominator. In this section, we will outline a process called polynomial long divisionThe process of dividing two polynomials using the division algorithm., which is based on the division algorithm for real numbers. For the sake of clarity, we will assume that all expressions in the denominator are nonzero.
Example 14
Divide:
Solution:
Here is the divisor and is the dividend. To determine the first term of the quotient, divide the leading term of the dividend by the leading term of the divisor.

Multiply the first term of the quotient by the divisor, remembering to distribute, and line up like terms with the dividend.

Subtract the resulting quantity from the dividend. Take care to subtract both terms.

Bring down the remaining terms and repeat the process.
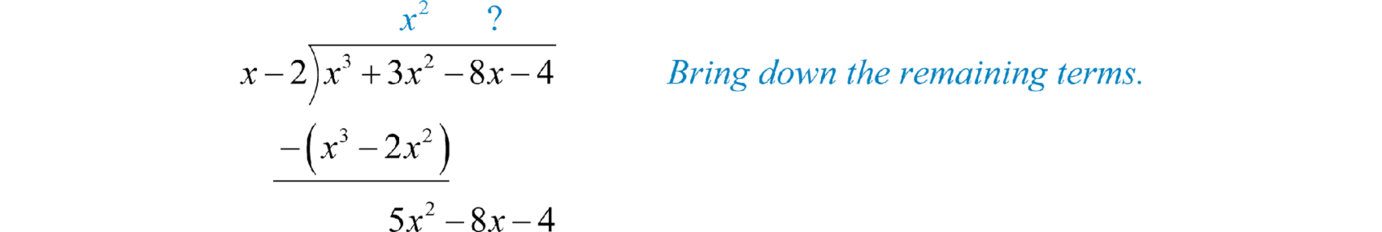
Notice that the leading term is eliminated and that the result has a degree that is one less. The complete process is illustrated below:
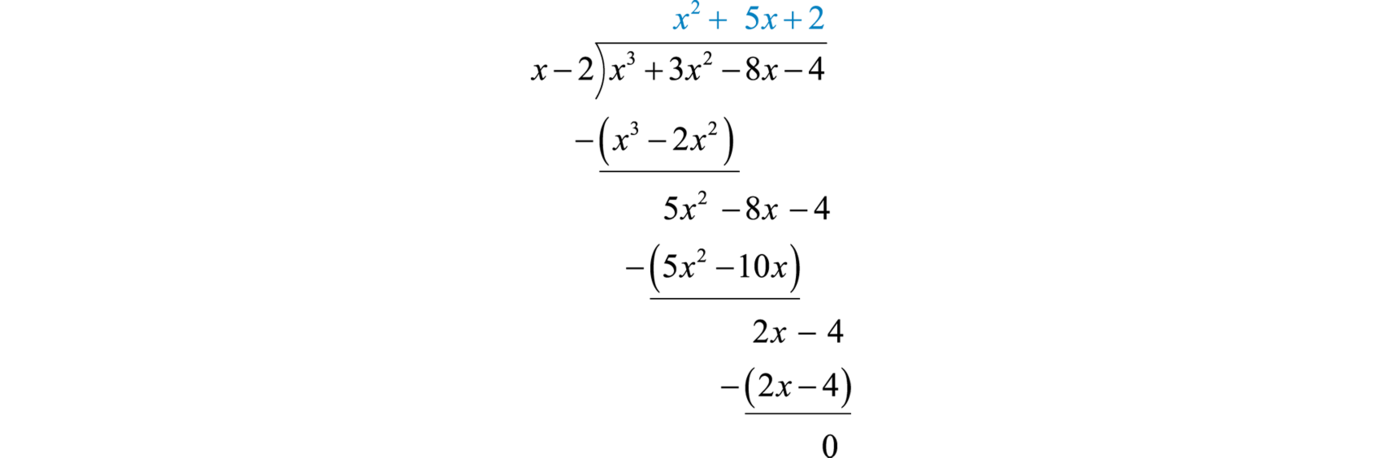
Polynomial long division ends when the degree of the remainder is less than the degree of the divisor. Here, the remainder is 0. Therefore, the binomial divides the polynomial evenly and the answer is the quotient shown above the division bar.
To check the answer, multiply the divisor by the quotient to see if you obtain the dividend as illustrated below:
This is left to the reader as an exercise.
Answer:
Next, we demonstrate the case where there is a nonzero remainder.

Just as with real numbers, the final answer adds to the quotient the fraction where the remainder is the numerator and the divisor is the denominator. In general, when dividing we have: If we multiply both sides by the divisor we obtain,
Example 15
Divide:
Solution:
Since the denominator is a binomial, begin by setting up polynomial long division.
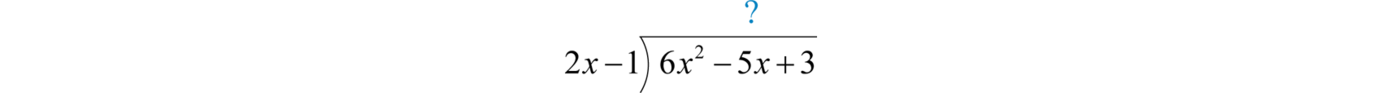
To start, determine what monomial times results in a leading term This is the quotient of the given leading terms: Multiply times the divisor , and line up the result with like terms of the dividend.
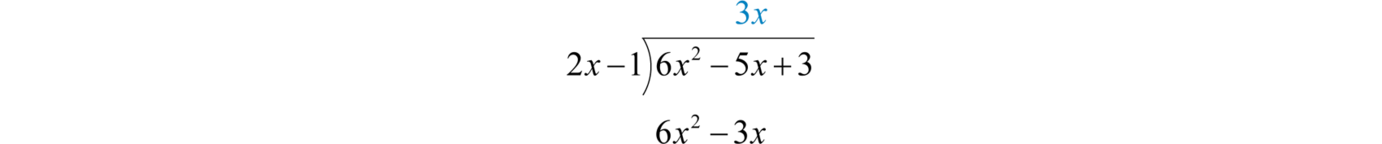
Subtract the result from the dividend and bring down the constant term +3.
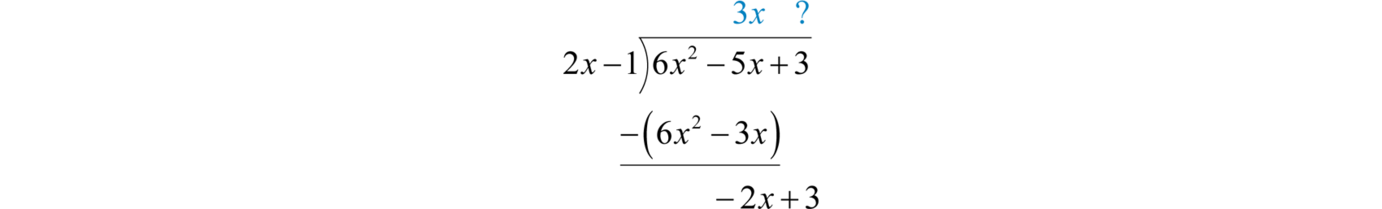
Subtracting eliminates the leading term. Multiply by −1 and line up the result.
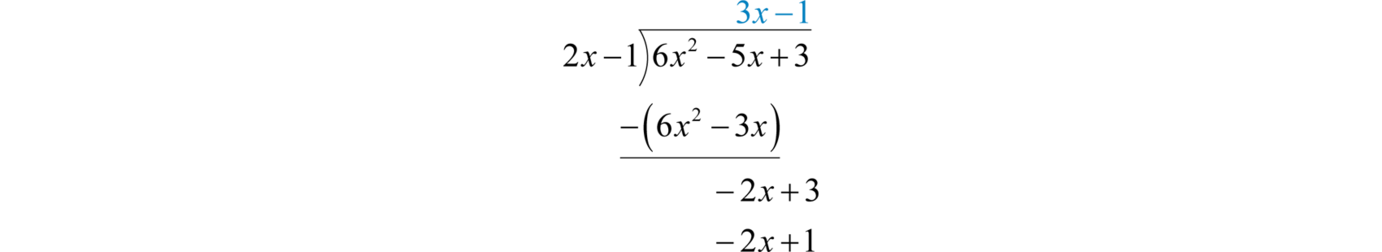
Subtract again and notice that we are left with a remainder.
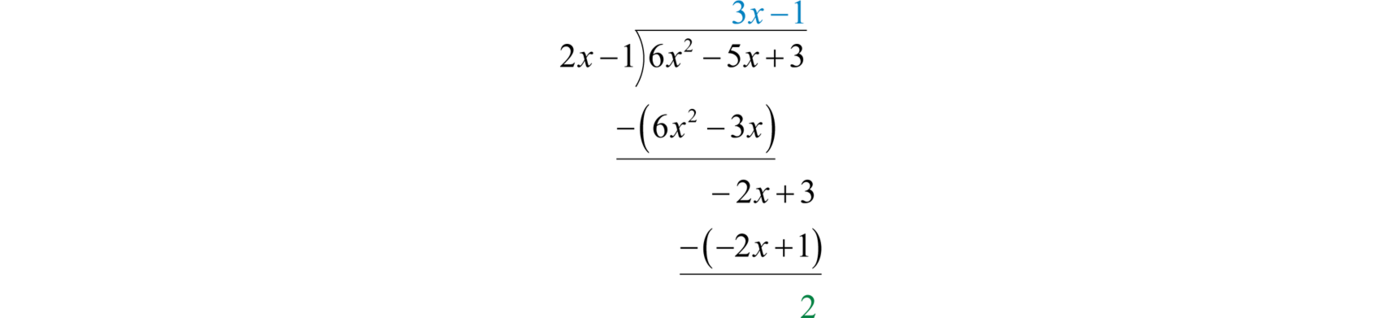
The constant term 2 has degree 0 and thus the division ends. Therefore,
To check that this result is correct, we multiply as follows:
Answer:
Occasionally, some of the powers of the variables appear to be missing within a polynomial. This can lead to errors when lining up like terms. Therefore, when first learning how to divide polynomials using long division, fill in the missing terms with zero coefficients, called placeholdersTerms with zero coefficients used to fill in all missing exponents within a polynomial..
Example 16
Divide:
Solution:
Notice that the binomial in the numerator does not have terms with degree 2 or 1. The division is simplified if we rewrite the expression with placeholders:
Set up polynomial long division:
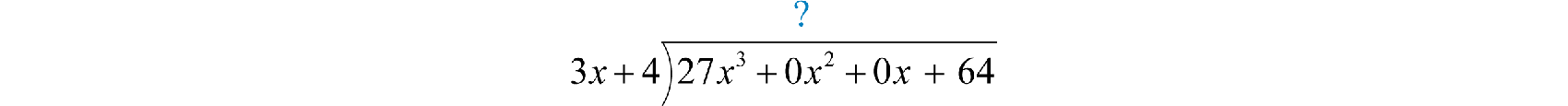
We begin with and work the rest of the division algorithm.
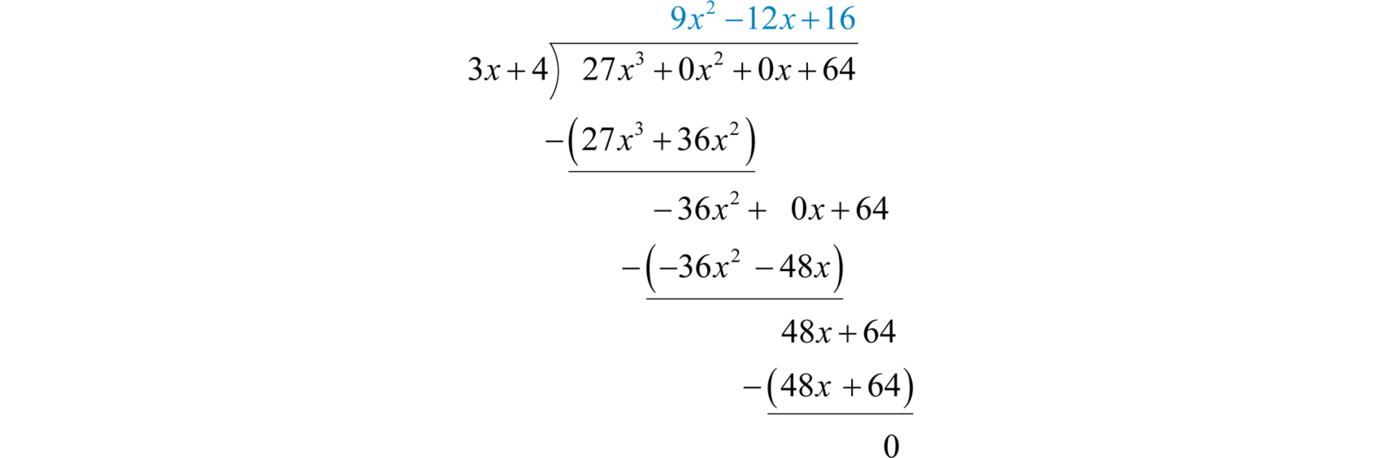
Answer:
Example 17
Divide:
Solution:
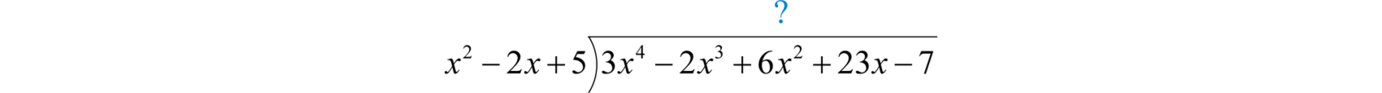
Begin the process by dividing the leading terms to determine the leading term of the quotient Take care to distribute and line up the like terms. Continue the process until the remainder has a degree less than 2.
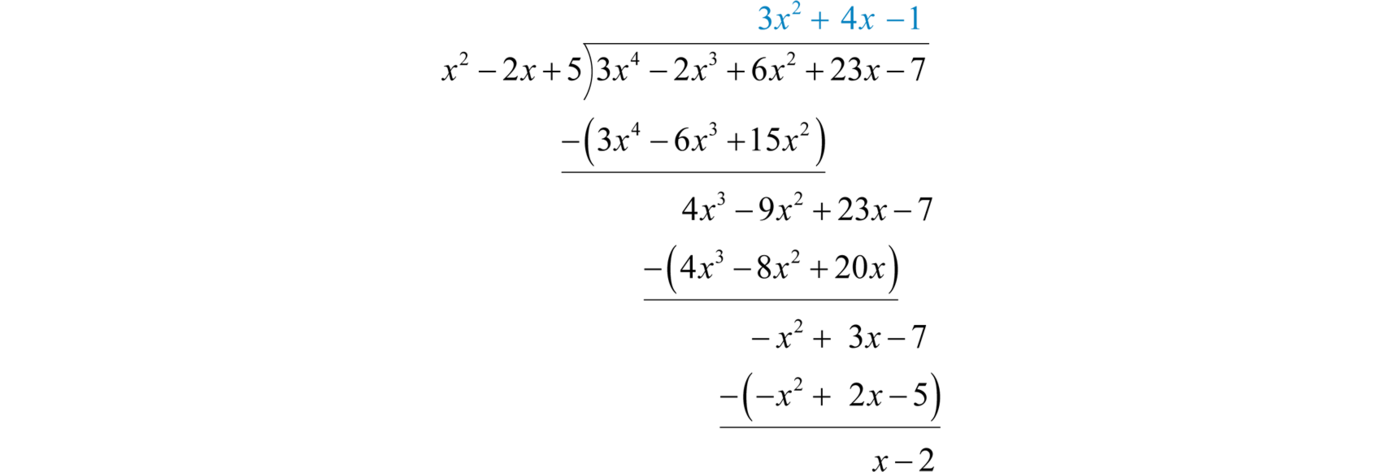
The remainder is Write the answer with the remainder:
Answer:
Polynomial long division takes time and practice to master. Work lots of problems and remember that you may check your answers by multiplying the quotient by the divisor (and adding the remainder if present) to obtain the dividend.
Key Takeaways
- Polynomials are special algebraic expressions where the terms are the products of real numbers and variables with whole number exponents.
- The degree of a polynomial with one variable is the largest exponent of the variable found in any term. In addition, the terms of a polynomial are typically arranged in descending order based on the degree of each term.
- When adding polynomials, remove the associated parentheses and then combine like terms. When subtracting polynomials, distribute the −1, remove the parentheses, and then combine like terms.
- To multiply polynomials apply the distributive property; multiply each term in the first polynomial with each term in the second polynomial. Then combine like terms.
- When dividing by a monomial, divide all terms in the numerator by the monomial and then simplify each term.
- When dividing a polynomial by another polynomial, apply the division algorithm.
Topic Exercises
-
-
-
-
-
-
-
-
-
-
-
-
5
-
-
-
-
-
-
-
-
Part A: Definitions
Write the given polynomials in standard form.
Classify the given polynomial as a monomial, binomial, or trinomial and state the degree.
State whether the polynomial is linear or quadratic and give the leading coefficient.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Subtract from
-
Subtract from
-
A right circular cylinder has a height that is equal to the radius of the base, Find a formula for the surface area in terms of h.
-
A rectangular solid has a width that is twice the height and a length that is 3 times that of the height. Find a formula for the surface area in terms of the height.
Part B: Adding and Subtracting Polynomials
Simplify.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Find the product of and
-
Find the product of and
-
Each side of a square measures units. Determine the area in terms of x.
-
Each edge of a cube measures units. Determine the volume in terms of x.
Part C: Multiplying Polynomials
Multiply.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Find the quotient of and
-
Find the quotient of and
Part D: Dividing Polynomials
Divide.
Answers
-
-
-
-
-
-
-
Trinomial; degree 2
-
-
Trinomial; degree 4
-
-
Binomial; degree 4
-
-
Quadratic, −9
-
-
Linear, 2
-
-
Quadratic, 5
-
-
Quadratic, −2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
square units
-
1.7 Solving Linear Equations
Learning Objectives
- Use the properties of equality to solve basic linear equations.
- Identify and solve conditional linear equations, identities, and contradictions.
- Clear fractions from equations.
- Set up and solve linear applications.
Solving Basic Linear Equations
An equationStatement indicating that two algebraic expressions are equal. is a statement indicating that two algebraic expressions are equal. A linear equation with one variableAn equation that can be written in the standard form , where a and b are real numbers and , x, is an equation that can be written in the standard form where a and b are real numbers and For example,
A solutionAny value that can replace the variable in an equation to produce a true statement. to a linear equation is any value that can replace the variable to produce a true statement. The variable in the linear equation is x and the solution is To verify this, substitute the value 4 in for x and check that you obtain a true statement.
Alternatively, when an equation is equal to a constant, we may verify a solution by substituting the value in for the variable and showing that the result is equal to that constant. In this sense, we say that solutions “satisfy the equation.”
Example 1
Is a solution to ?
Solution:
Recall that when evaluating expressions, it is a good practice to first replace all variables with parentheses, and then substitute the appropriate values. By making use of parentheses, we avoid some common errors when working the order of operations.
Answer: No, does not satisfy the equation.
Developing techniques for solving various algebraic equations is one of our main goals in algebra. This section reviews the basic techniques used for solving linear equations with one variable. We begin by defining equivalent equationsEquations with the same solution set. as equations with the same solution set.
Here we can see that the three linear equations are equivalent because they share the same solution set, namely, {7}. To obtain equivalent equations, use the following properties of equalityProperties that allow us to obtain equivalent equations by adding, subtracting, multiplying, and dividing both sides of an equation by nonzero real numbers.. Given algebraic expressions A and B, where c is a nonzero number:
Addition property of equality: |
|
Subtraction property of equality: |
|
Multiplication property of equality: |
|
Division property of equality: |
Note: Multiplying or dividing both sides of an equation by 0 is carefully avoided. Dividing by 0 is undefined and multiplying both sides by 0 results in the equation 0 = 0.
We solve algebraic equations by isolating the variable with a coefficient of 1. If given a linear equation of the form , then we can solve it in two steps. First, use the appropriate equality property of addition or subtraction to isolate the variable term. Next, isolate the variable using the equality property of multiplication or division. Checking the solution in the following examples is left to the reader.
Example 2
Solve:
Solution:
Answer: The solution is 3.
Example 3
Solve:
Solution:
When no sign precedes the term, it is understood to be positive. In other words, think of this as Therefore, we begin by subtracting 8 on both sides of the equal sign.
It does not matter on which side we choose to isolate the variable because the symmetric propertyAllows you to solve for the variable on either side of the equal sign, because is equivalent to states that is equivalent to
Answer: The solution is 4.
Example 4
Solve:
Solution:
Isolate the variable term using the addition property of equality, and then multiply both sides of the equation by the reciprocal of the coefficient
Answer: The solution is −6.
In summary, to retain equivalent equations, we must perform the same operation on both sides of the equation.
General Guidelines for Solving Linear Equations
Typically linear equations are not given in standard form, and so solving them requires additional steps. When solving linear equations, the goal is to determine what value, if any, will produce a true statement when substituted in the original equation. Do this by isolating the variable using the following steps:
- Step 1: Simplify both sides of the equation using the order of operations and combine all like terms on the same side of the equal sign.
- Step 2: Use the appropriate properties of equality to combine like terms on opposite sides of the equal sign. The goal is to obtain the variable term on one side of the equation and the constant term on the other.
- Step 3: Divide or multiply as needed to isolate the variable.
- Step 4: Check to see if the answer solves the original equation.
We will often encounter linear equations where the expressions on each side of the equal sign can be simplified. If this is the case, then it is best to simplify each side first before solving. Normally this involves combining same-side like terms.
Note: At this point in our study of algebra the use of the properties of equality should seem routine. Therefore, displaying these steps in this text, usually in blue, becomes optional.
Example 5
Solve:
Solution:
First combine the like terms on the left side of the equal sign.
Always use the original equation to check to see if the solution is correct.
Answer: The solution is
Given a linear equation in the form , we begin the solving process by combining like terms on opposite sides of the equal sign. To do this, use the addition or subtraction property of equality to place like terms on the same side so that they can be combined. In the examples that remain, the check is left to the reader.
Example 6
Solve:
Solution:
Subtract on both sides so that we can combine the terms involving y on the left side.
From here, solve using the techniques developed previously.
Answer: The solution is −2.
Solving will often require the application of the distributive property.
Example 7
Solve:
Solution:
Simplify the linear expressions on either side of the equal sign first.
Answer: The solution is
Example 8
Solve:
Solution:
Begin by applying the distributive property.
Here we point out that is equivalent to ; therefore, we choose to divide both sides of the equation by −1.
Alternatively, we can multiply both sides of by negative one and achieve the same result.
Answer: The solution is 2.
There are three different types of equations. Up to this point, we have been solving conditional equationsEquations that are true for particular values.. These are equations that are true for particular values. An identityAn equation that is true for all possible values. is an equation that is true for all possible values of the variable. For example, has a solution set consisting of all real numbers, A contradictionAn equation that is never true and has no solution. is an equation that is never true and thus has no solutions. For example, has no solution. We use the empty set, , to indicate that there are no solutions.
If the end result of solving an equation is a true statement, like 0 = 0, then the equation is an identity and any real number is a solution. If solving results in a false statement, like 0 = 1, then the equation is a contradiction and there is no solution.
Example 9
Solve:
Solution:
Solving leads to a false statement; therefore, the equation is a contradiction and there is no solution.
Answer:
Example 10
Solve:
Solution:
Solving leads to a true statement; therefore, the equation is an identity and any real number is a solution.
Answer:
The coefficients of linear equations may be any real number, even decimals and fractions. When this is the case it is possible to use the multiplication property of equality to clear the fractional coefficients and obtain integer coefficients in a single step. If given fractional coefficients, then multiply both sides of the equation by the least common multiple of the denominators (LCD).
Example 11
Solve:
Solution:
Clear the fractions by multiplying both sides by the least common multiple of the given denominators. In this case, it is the
Answer: The solution is −9.
It is important to know that this technique only works for equations. Do not try to clear fractions when simplifying expressions. As a reminder:
Expression |
Equation |
|---|---|
We simplify expressions and solve equations. If you multiply an expression by 6, you will change the problem. However, if you multiply both sides of an equation by 6, you obtain an equivalent equation.
Incorrect |
Correct |
|---|---|
Applications Involving Linear Equations
Algebra simplifies the process of solving real-world problems. This is done by using letters to represent unknowns, restating problems in the form of equations, and by offering systematic techniques for solving those equations. To solve problems using algebra, first translate the wording of the problem into mathematical statements that describe the relationships between the given information and the unknowns. Usually, this translation to mathematical statements is the difficult step in the process. The key to the translation is to carefully read the problem and identify certain key words and phrases.
Key Words |
Translation |
|---|---|
Sum, increased by, more than, plus, added to, total |
+ |
Difference, decreased by, subtracted from, less, minus |
− |
Product, multiplied by, of, times, twice |
|
Quotient, divided by, ratio, per |
|
Is, total, result |
= |
When translating sentences into mathematical statements, be sure to read the sentence several times and parse out the key words and phrases. It is important to first identify the variable, “let x represent…” and state in words what the unknown quantity is. This step not only makes our work more readable, but also forces us to think about what we are looking for.
Example 12
When 6 is subtracted from twice the sum of a number and 8 the result is 5. Find the number.
Solution:
Let n represent the unknown number.
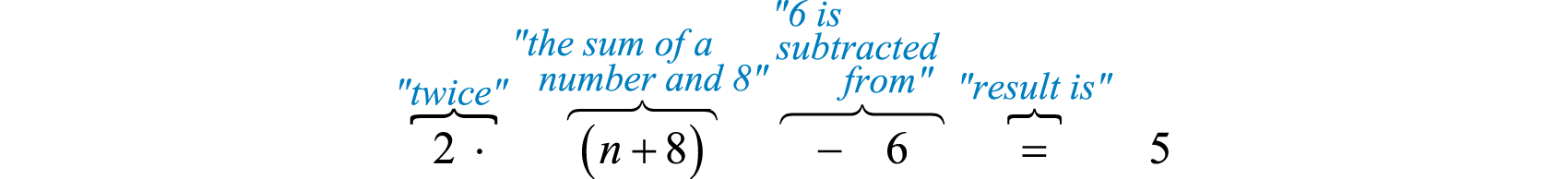
To understand why we included the parentheses in the set up, you must study the structure of the following two sentences and their translations:
“twice the sum of a number and 8” |
|
“the sum of twice a number and 8” |
The key was to focus on the phrase “twice the sum,” this prompted us to group the sum within parentheses and then multiply by 2. After translating the sentence into a mathematical statement we then solve.
Check.
Answer: The number is
General guidelines for setting up and solving word problems follow.
- Step 1: Read the problem several times, identify the key words and phrases, and organize the given information.
- Step 2: Identify the variables by assigning a letter or expression to the unknown quantities.
- Step 3: Translate and set up an algebraic equation that models the problem.
- Step 4: Solve the resulting algebraic equation.
- Step 5: Finally, answer the question in sentence form and make sure it makes sense (check it).
For now, set up all of your equations using only one variable. Avoid two variables by looking for a relationship between the unknowns.
Example 13
A rectangle has a perimeter measuring 92 meters. The length is 2 meters less than 3 times the width. Find the dimensions of the rectangle.
Solution:
The sentence “The length is 2 meters less than 3 times the width,” gives us the relationship between the two variables.
Let w represent the width of the rectangle.
Let represent the length.

The sentence “A rectangle has a perimeter measuring 92 meters” suggests an algebraic set up. Substitute 92 for the perimeter and the expression for the length into the appropriate formula as follows:
Once you have set up an algebraic equation with one variable, solve for the width, w.
Use to find the length.
To check, make sure the perimeter is 92 meters.
Answer: The rectangle measures 12 meters by 34 meters.
Example 14
Given a annual interest rate, how long will it take $2,500 to yield $437.50 in simple interest?
Solution:
Let t represent the time needed to earn $437.50 at Organize the information needed to use the formula for simple interest,
Given interest for the time period: |
|
Given principal: |
|
Given rate: |
Next, substitute all of the known quantities into the formula and then solve for the only unknown, t.
Answer: It takes 4 years for $2,500 invested at to earn $437.50 in simple interest.
Example 15
Susan invested her total savings of $12,500 in two accounts earning simple interest. Her mutual fund account earned 7% last year and her CD earned 4.5%. If her total interest for the year was $670, how much was in each account?
Solution:
The relationship between the two unknowns is that they total $12,500. When a total is involved, a common technique used to avoid two variables is to represent the second unknown as the difference of the total and the first unknown.
Let x represent the amount invested in the mutual fund.
Let 12,500 − x represent the remaining amount invested in the CD.
Organize the data.
Interest earned in the mutual fund: |
|
Interest earned in the CD: |
|
Total interest: |
The total interest is the sum of the interest earned from each account.
This equation models the problem with one variable. Solve for x.
Use to find the amount in the CD.
Answer: Susan invested $4,300 at 7% in a mutual fund and $8,200 at 4.5% in a CD.
Key Takeaways
- Solving general linear equations involves isolating the variable, with coefficient 1, on one side of the equal sign. To do this, first use the appropriate equality property of addition or subtraction to isolate the variable term on one side of the equal sign. Next, isolate the variable using the equality property of multiplication or division. Finally, check to verify that your solution solves the original equation.
- If solving a linear equation leads to a true statement like 0 = 0, then the equation is an identity and the solution set consists of all real numbers,
- If solving a linear equation leads to a false statement like 0 = 5, then the equation is a contradiction and there is no solution,
- Clear fractions by multiplying both sides of an equation by the least common multiple of all the denominators. Distribute and multiply all terms by the LCD to obtain an equivalent equation with integer coefficients.
- Simplify the process of solving real-world problems by creating mathematical models that describe the relationship between unknowns. Use algebra to solve the resulting equations.
Topic Exercises
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Solve for x:
-
Solve for x:
Part A: Solving Basic Linear Equations
Determine whether or not the given value is a solution.
Solve.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Solve for w:
-
Solve for a:
-
Solve for t:
-
Solve for w:
-
Solve for b:
-
Solve for a:
-
Solve for a:
-
Solve for h:
-
Solve for F:
-
Solve for x:
Part B: Solving Linear Equations
Solve.
-
When 3 is subtracted from the sum of a number and 10 the result is 2. Find the number.
-
The sum of 3 times a number and 12 is equal to 3. Find the number.
-
Three times the sum of a number and 6 is equal to 5 times the number. Find the number.
-
Twice the sum of a number and 4 is equal to 3 times the sum of the number and 1. Find the number.
-
A larger integer is 1 more than 3 times another integer. If the sum of the integers is 57, find the integers.
-
A larger integer is 5 more than twice another integer. If the sum of the integers is 83, find the integers.
-
One integer is 3 less than twice another integer. Find the integers if their sum is 135.
-
One integer is 10 less than 4 times another integer. Find the integers if their sum is 100.
-
The sum of three consecutive integers is 339. Find the integers.
-
The sum of four consecutive integers is 130. Find the integers.
-
The sum of three consecutive even integers is 174. Find the integers.
-
The sum of four consecutive even integers is 116. Find the integers.
-
The sum of three consecutive odd integers is 81. Find the integers.
-
The sum of four consecutive odd integers is 176. Find the integers.
-
The length of a rectangle is 5 centimeters less than twice its width. If the perimeter is 134 centimeters, find the length and width.
-
The length of a rectangle is 4 centimeters more than 3 times its width. If the perimeter is 64 centimeters, find the length and width.
-
The width of a rectangle is one-half that of its length. If the perimeter measures 36 inches, find the dimensions of the rectangle.
-
The width of a rectangle is 4 inches less than its length. If the perimeter measures 72 inches, find the dimensions of the rectangle.
-
The perimeter of a square is 48 inches. Find the length of each side.
-
The perimeter of an equilateral triangle is 96 inches. Find the length of each side.
-
The circumference of a circle measures units. Find the radius.
-
The circumference of a circle measures 25 centimeters. Find the radius rounded off to the nearest hundredth.
-
For how many years must $1,000 be invested at % to earn $165 in simple interest?
-
For how many years must $20,000 be invested at % to earn $3,125 in simple interest?
-
At what annual interest rate must $6500 be invested for 2 years to yield $1,040 in simple interest?
-
At what annual interest rate must $5,750 be invested for 1 year to yield $333.50 in simple interest?
-
If the simple interest earned for 5 years was $1,860 and the annual interest rate was 6%, what was the principal?
-
If the simple interest earned for 2 years was $543.75 and the annual interest rate was , what was the principal?
-
How many years will it take $600 to double earning simple interest at a 5% annual rate? (Hint: To double, the investment must earn $600 in simple interest.)
-
How many years will it take $10,000 to double earning simple interest at a 5% annual rate? (Hint: To double, the investment must earn $10,000 in simple interest.)
-
Jim invested $4,200 in two accounts. One account earns 3% simple interest and the other earns 6%. If the interest after 1 year was $159, how much did he invest in each account?
-
Jane has her $6,500 savings invested in two accounts. She has part of it in a CD at 5% annual interest and the rest in a savings account that earns 4% annual interest. If the simple interest earned from both accounts is $303 for the year, then how much does she have in each account?
-
Jose put last year’s bonus of $8,400 into two accounts. He invested part in a CD with 2.5% annual interest and the rest in a money market fund with 1.5% annual interest. His total interest for the year was $198. How much did he invest in each account?
-
Mary invested her total savings of $3,300 in two accounts. Her mutual fund account earned 6.2% last year and her CD earned 2.4%. If her total interest for the year was $124.80, how much was in each account?
-
Alice invests money into two accounts, one with 3% annual interest and another with 5% annual interest. She invests 3 times as much in the higher yielding account as she does in the lower yielding account. If her total interest for the year is $126, how much did she invest in each account?
-
James invested an inheritance in two separate banks. One bank offered % annual interest rate and the other %. He invested twice as much in the higher yielding bank account than he did in the other. If his total simple interest for 1 year was $5,760, then what was the amount of his inheritance?
-
If it takes Jim hours to drive the 40 miles to work, then what is Jim’s average speed?
-
It took Jill hours to drive the 189 miles home from college. What was her average speed?
-
At what speed should Jim drive if he wishes to travel 176 miles in hours?
-
James and Martin were able to drive the 1,140 miles from Los Angeles to Seattle. If the total trip took 19 hours, then what was their average speed?
Part C: Applications
Set up an algebraic equation then solve.
Number Problems
Geometry Problems
Simple Interest Problems
Uniform Motion Problems
-
What is regarded as the main business of algebra? Explain.
-
What is the origin of the word algebra?
-
Create an identity or contradiction of your own and share it on the discussion board. Provide a solution and explain how you found it.
-
Post something you found particularly useful or interesting in this section. Explain why.
-
Conduct a web search for “solving linear equations.” Share a link to website or video tutorial that you think is helpful.
Part D: Discussion Board
Answers
-
No
-
-
Yes
-
-
No
-
-
Yes
-
-
6
-
-
-
-
0
-
-
-
-
-
-
−3
-
-
−15
-
-
-
-
3
-
-
−5
-
-
-
-
-
-
-
-
2.5
-
-
Ø
-
-
3
-
-
2
-
-
Ø
-
-
-
-
−81
-
-
1.2
-
-
-
-
0
-
-
Ø
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
−5
-
-
9
-
-
14, 43
-
-
46, 89
-
-
112, 113, 114
-
-
56, 58, 60
-
-
25, 27, 29
-
-
Width: 24 centimeters; length: 43 centimeters
-
-
Width: 6 inches; length: 12 inches
-
-
12 inches
-
-
40 units
-
-
3 years
-
-
8%
-
-
$6,200
-
-
20 years
-
-
He invested $3,100 at 3% and $1,100 at 6%.
-
-
Jose invested $7,200 in the CD and $1,200 in the money market fund.
-
-
Alice invested $700 at 3% and $2,100 at 5%.
-
-
32 miles per hour
-
-
64 miles per hour
-
-
Answer may vary
-
-
Answer may vary
-
-
Answer may vary
1.8 Solving Linear Inequalities with One Variable
Learning Objectives
- Identify linear inequalities and check solutions.
- Solve linear inequalities and express the solutions graphically on a number line and in interval notation.
- Solve compound linear inequalities and express the solutions graphically on a number line and in interval notation.
- Solve applications involving linear inequalities and interpret the results.
Linear Inequalities
A linear inequalityLinear expressions related with the symbols , <, , and >. is a mathematical statement that relates a linear expression as either less than or greater than another. The following are some examples of linear inequalities, all of which are solved in this section:
A solution to a linear inequalityA real number that produces a true statement when its value is substituted for the variable. is a real number that will produce a true statement when substituted for the variable. Linear inequalities have either infinitely many solutions or no solution. If there are infinitely many solutions, graph the solution set on a number line and/or express the solution using interval notation.
Example 1
Are and solutions to ?
Solution:
Substitute the values in for x, simplify, and check to see if we obtain a true statement.
Check |
Check |
|---|---|
Answer: is a solution and is not.
All but one of the techniques learned for solving linear equations apply to solving linear inequalities. You may add or subtract any real number to both sides of an inequality, and you may multiply or divide both sides by any positive real number to create equivalent inequalities. For example:
Subtracting 7 from each side and dividing each side by positive 5 results in an inequality that is true.
Example 2
Solve and graph the solution set:
Solution:

It is helpful to take a minute and choose a few values in and out of the solution set, substitute them into the original inequality, and then verify the results. As indicated, you should expect to solve the original inequality and that should not.
Check |
Check |
|---|---|
Checking in this manner gives us a good indication that we have solved the inequality correctly.
We can express this solution in two ways: using set notation and interval notation.
In this text we will choose to present answers using interval notation.
Answer:
When working with linear inequalities, a different rule applies when multiplying or dividing by a negative number. To illustrate the problem, consider the true statement and divide both sides by −5.
Dividing by −5 results in a false statement. To retain a true statement, the inequality must be reversed.
The same problem occurs when multiplying by a negative number. This leads to the following new rule: when multiplying or dividing by a negative number, reverse the inequality. It is easy to forget to do this so take special care to watch for negative coefficients. In general, given algebraic expressions A and B, where c is a positive nonzero real number, we have the following properties of inequalitiesProperties used to obtain equivalent inequalities and used as a means to solve them.:
Addition property of inequalities: |
|
Subtraction property of inequalities: |
|
Multiplication property of inequalities: |
|
Division property of inequalities: |
|
We use these properties to obtain an equivalent inequalityInequalities that share the same solution set., one with the same solution set, where the variable is isolated. The process is similar to solving linear equations.
Example 3
Solve and graph the solution set:
Solution:
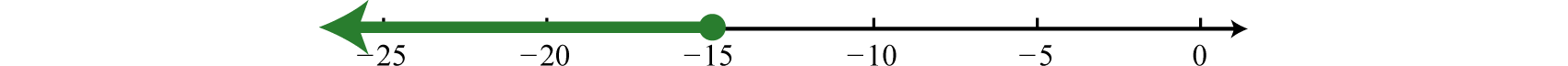
Answer: Interval notation
Example 4
Solve and graph the solution set:
Solution:

Answer: Interval notation
Example 5
Solve and graph the solution set:
Solution:

Answer: Interval notation:
Compound Inequalities
Following are some examples of compound linear inequalities:
These compound inequalitiesTwo or more inequalities in one statement joined by the word “and” or by the word “or.” are actually two inequalities in one statement joined by the word and or by the word or. For example, is a compound inequality because it can be decomposed as follows:
We can solve each inequality individually; the intersection of the two solution sets solves the original compound inequality. While this method works, there is another method that usually requires fewer steps. Apply the properties of this section to all three parts of the compound inequality with the goal of isolating the variable in the middle of the statement to determine the bounds of the solution set.
Example 6
Solve and graph the solution set:
Solution:

Answer: Interval notation:
Example 7
Solve and graph the solution set:
Solution:

Answer: Interval notation
It is important to note that when multiplying or dividing all three parts of a compound inequality by a negative number, you must reverse all of the inequalities in the statement. For example: The answer above can be written in an equivalent form, where smaller numbers lie to the left and the larger numbers lie to the right, as they appear on a number line. Using interval notation, write:
For compound inequalities with the word “or” you work both inequalities separately and then consider the union of the solution sets. Values in this union solve either inequality.
Example 8
Solve and graph the solution set:
Solution:
Solve each inequality and form the union by combining the solution sets.
or |
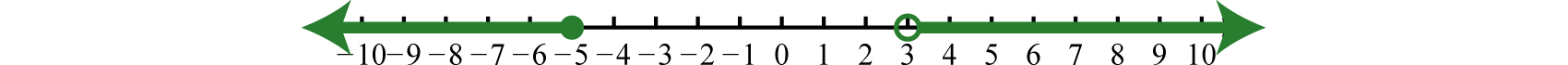
Answer: Interval notation
Applications of Linear Inequalities
Some of the key words and phrases that indicate inequalities are summarized below:
Key Phrases |
Translation |
|---|---|
A number is at least 5. |
|
A number is 5 or more inclusive. |
|
A number is at most 3. |
|
A number is 3 or less inclusive. |
|
A number is strictly less than 4. |
|
A number is less than 4, noninclusive. |
|
A number is greater than 7. |
|
A number is more than 7, noninclusive. |
|
A number is in between 2 and 10. |
|
A number is at least 5 and at most 15. |
|
A number may range from 5 to 15. |
As with all applications, carefully read the problem several times and look for key words and phrases. Identify the unknowns and assign variables. Next, translate the wording into a mathematical inequality. Finally, use the properties you have learned to solve the inequality and express the solution graphically or in interval notation.
Example 9
Seven less than 3 times the sum of a number and 5 is at most 11. Find all numbers that satisfy this condition.
Solution:
First, choose a variable for the unknown number and identify the key words and phrases.
Let n represent the unknown indicated by “a number.”

Solve for n.
Answer: Any number less than or equal to 1 will satisfy the statement.
Example 10
To earn a B in a mathematics course the test average must be at least 80% and less than 90%. If a student earned 92%, 96%, 79%, and 83% on the first four tests, what must she score on the fifth test to earn a B?
Solution:
Set up a compound inequality where the test average is between 80% and 90%. In this case, include the lower bound, 80.
Let x represent the score on the fifth test.
Answer: She must earn a score of at least 50% and less than 100%.
In the previous example, the upper bound 100% was not part of the solution set. What would happen if she did earn a 100% on the fifth test?
As we can see, her average would be 90%, which would earn her an A.
Key Takeaways
- Inequalities typically have infinitely many solutions. The solutions are presented graphically on a number line or using interval notation or both.
- All but one of the rules for solving linear inequalities are the same as solving linear equations. If you divide or multiply an inequality by a negative number, reverse the inequality to obtain an equivalent inequality.
- Compound inequalities involving the word “or” require us to solve each inequality and form the union of each solution set. These are the values that solve at least one of the given inequalities.
- Compound inequalities involving the word “and” require the intersection of the solution sets for each inequality. These are the values that solve both or all of the given inequalities.
- The general guidelines for solving word problems apply to applications involving inequalities. Be aware of a new list of key words and phrases that indicate a mathematical setup involving inequalities.
Topic Exercises
-
-
-
-
-
;
-
;
-
;
-
;
-
;
-
;
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Part A: Linear Inequalities
Determine whether or not the given value is a solution.
Graph all solutions on a number line and provide the corresponding interval notation.
Part B: Compound Inequalities
Graph all solutions on a number line and provide the corresponding interval notation.
-
Three less than twice the sum of a number and 6 is at most 13.
-
Five less than 3 times the sum of a number and 4 is at most 10.
-
Five times the sum of a number and 3 is at least 5.
-
Three times the difference between a number and 2 is at least 12.
-
The sum of 3 times a number and 8 is between 2 and 20.
-
Eight less than twice a number is between −20 and −8.
-
Four subtracted from three times some number is between −4 and 14.
-
Nine subtracted from 5 times some number is between 1 and 11.
-
With a golf club membership, costing $120 per month, each round of golf costs only $35.00. How many rounds of golf can a member play if he wishes to keep his costs $270 per month at most?
-
A rental truck costs $95 per day plus $0.65 per mile driven. How many miles can be driven on a one-day rental to keep the cost at most $120?
-
Mark earned 6, 7, and 10 points out of 10 on the first three quizzes. What must he score on the fourth quiz to average at least 8?
-
Joe earned scores of 78, 82, 88 and 70 on his first four algebra exams. What must he score on the fifth exam to average at least 80?
-
A gymnast scored 13.2, 13.0, 14.3, 13.8, and 14.6 on the first five events. What must he score on the sixth event to average at least 14.0?
-
A dancer scored 7.5 and 8.2 from the first two judges. What must her score from the third judge come in as if she is to average 8.4 or higher?
-
If two times an angle is between 180 degrees and 270 degrees, then what are the bounds of the original angle?
-
The perimeter of a square must be between 120 inches and 460 inches. Find the length of all possible sides that satisfy this condition.
-
A computer is set to shut down if the temperature exceeds 45°C. Give an equivalent statement using degrees Fahrenheit. Hint:
-
A certain antifreeze is effective for a temperature range of −35°C to 120°C. Find the equivalent range in degrees Fahrenheit.
Part C: Applications
Find all numbers that satisfy the given condition.
Set up an algebraic inequality and then solve.
-
Often students reverse the inequality when solving ? Why do you think this is a common error? Explain to a beginning algebra student why we do not.
-
Conduct a web search for “solving linear inequalities.” Share a link to website or video tutorial that you think is helpful.
-
Write your own 5 key takeaways for this entire chapter. What did you find to be review and what did you find to be new? Share your thoughts on the discussion board.
Part D: Discussion Board
Answers
-
Yes
-
-
No
-
-
Yes
-
-
No
-
-
Yes
-
-
;

-
-
;
-
-
;

-
-
;

-
-
;

-
-
;
-
-
;

-
-
;
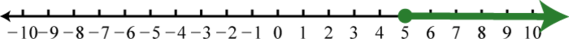
-
-
;

-
-
;

-
-
;
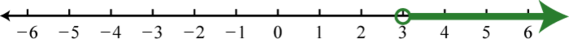
-
-
;
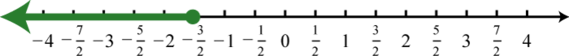
-
-
Ø;
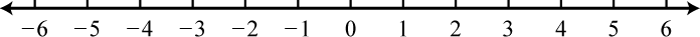
-
-
;

-
-
;

-
-
;

-
-
;

-
-
;

-
-
;

-
-
;

-
-
;

-
-
;
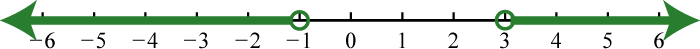
-
-
;

-
-
;

-
-
;

-
-
;
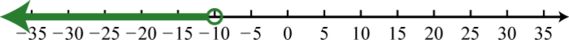
-
-
;

-
-
;

-
-
Ø;
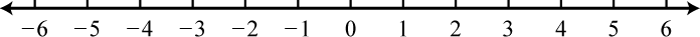
-
-
−2;
-
-
;

-
-
;

-
-
;
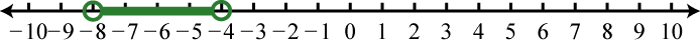
-
-
;
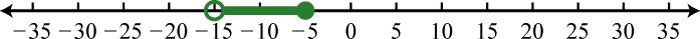
-
-
;

-
-
;

-
-
-
-
-
-
-
-
-
-
Members may play 4 rounds or fewer.
-
-
Mark must earn at least 9 points on the fourth quiz.
-
-
He must score a 15.1 on the sixth event.
-
-
The angle is between 90 degrees and 135 degrees.
-
-
The computer will shut down when the temperature exceeds 113°F.
-
-
Answer may vary
-
-
Answer may vary
1.9 Review Exercises and Sample Exam
Review Exercises
Review of Real Numbers and Absolute Value
Reduce to lowest terms.
Simplify.
Graph the solution set and give the interval notation equivalent.
Determine the inequality that corresponds to the set expressed using interval notation.
Simplify.
Determine the values represented by a.
Operations with Real Numbers
Perform the operations.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Find the length of the diagonal of a square with sides measuring 8 centimeters.
-
Find the length of the diagonal of a rectangle with sides measuring 6 centimeters and 12 centimeters.
Square and Cube Roots of Real Numbers
Simplify.
Use a calculator to approximate the following to the nearest thousandth.
-
-
-
-
-
-
-
-
-
-
-
-
-
where
-
where
-
where and
-
where and
-
where
-
where
-
where , , and
-
where , , and
-
where and
-
where
-
What is the simple interest earned on a 4 year investment of $4,500 at an annual interest rate of %?
-
James traveled at an average speed of 48 miles per hour for hours. How far did he travel?
-
The period of a pendulum T in seconds is given by the formula where L represents its length in feet. Approximate the period of a pendulum with length 2 feet. Round off to the nearest tenth of a foot.
-
The average distance d, in miles, a person can see an object is given by the formula where h represents the person’s height above the ground, measured in feet. What average distance can a person see an object from a height of 10 feet? Round off to the nearest tenth of a mile.
Algebraic Expressions and Formulas
Multiply.
Combine like terms.
Simplify.
Evaluate.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
The value of a new tablet computer in dollars can be estimated using the formula where t represents the number of years after it is purchased. Use the formula to estimate the value of the tablet computer years after it was purchased.
-
The speed of light is approximately miles per hour. Express this speed in miles per minute and determine the distance light travels in 4 minutes.
Rules of Exponents and Scientific Notation
Multiply.
Perform the operations.
Polynomials and Their Operations
Simplify.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Solve for s:
-
Solve for x:
-
A larger integer is 3 more than twice another. If their sum divided by 2 is 9, find the integers.
-
The sum of three consecutive odd integers is 171. Find the integers.
-
The length of a rectangle is 3 meters less than twice its width. If the perimeter measures 66 meters, find the length and width.
-
How long will it take $500 to earn $124 in simple interest earning 6.2% annual interest?
-
It took Sally hours to drive the 147 miles home from her grandmother’s house. What was her average speed?
-
Jeannine invested her bonus of $8,300 in two accounts. One account earned % simple interest and the other earned % simple interest. If her total interest for one year was $341.75, how much did she invest in each account?
Solving Linear Equations
Solve.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Jerry scored 90, 85, 92, and 76 on the first four algebra exams. What must he score on the fifth exam so that his average is at least 80?
-
If 6 degrees less than 3 times an angle is between 90 degrees and 180 degrees, then what are the bounds of the original angle?
Solving Linear Inequalities with One Variable
Solve. Graph all solutions on a number line and provide the corresponding interval notation.
Answers
-
-
-
-
-
-
-
-
-
;

-
-
;

-
-
;
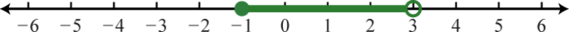
-
-
;
-
-
-
-
-
-
-
-
-
-
-
-
4
-
-
-
-
-
-
-
-
−4
-
-
-
-
−15
-
-
−6
-
-
−24
-
-
-
-
−50
-
-
14
-
-
-
-
0
-
-
-
-
-
-
-
-
-
-
3.464
-
-
2.621
-
-
centimeters
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
80
-
-
30
-
-
-
-
-
-
$855
-
-
1.6 seconds
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
$128.57
-
-
-
-
-
-
-
-
-
-
Ø
-
-
−3
-
-
-
-
-
-
-
-
5, 13
-
-
Length: 21 meters; Width: 12 meters
-
-
42 miles per hour
-
-
;

-
-
;
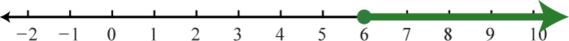
-
-
;

-
-
;
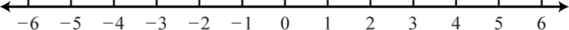
-
-
;

-
-
;

-
-
;

-
-
;

-
-
;

-
-
;

-
-
;

-
-
Jerry must score at least 57 on the fifth exam.
-
Sample Exam
-
-
-
-
-
Find the diagonal of a square with sides measuring 6 centimeters.
-
-
-
-
-
-
-
-
-
-
-
-
Solve for y:
-
-
-
-
-
Degrees Fahrenheit F is given by the formula where C represents degrees Celsius. What is the Fahrenheit equivalent to 35° Celsius?
-
The length of a rectangle is 5 inches less than its width. If the perimeter is 134 inches, find the length and width of the rectangle.
-
Melanie invested 4,500 in two separate accounts. She invested part in a CD that earned 3.2% simple interest and the rest in a savings account that earned 2.8% simple interest. If the total simple interest for one year was $138.80, how much did she invest in each account?
-
A rental car costs $45.00 per day plus $0.48 per mile driven. If the total cost of a one-day rental is to be at most $105, how many miles can be driven?
Simplify.
Simplify.
Solve.
Solve. Graph the solutions on a number line and give the corresponding interval notation.
Use algebra to solve the following.
Answers
-
38
-
-
-
-
centimeters
-
-
-
-
-
-
-
-
-
-
-
-
-
-
;
-
-
;

-
-
Length: 31 inches; width: 36 inches
-
-
The car can be driven at most 125 miles.