This is “Review Exercises and Sample Exam”, section 1.9 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
1.9 Review Exercises and Sample Exam
Review Exercises
Review of Real Numbers and Absolute Value
Reduce to lowest terms.
Simplify.
Graph the solution set and give the interval notation equivalent.
Determine the inequality that corresponds to the set expressed using interval notation.
Simplify.
Determine the values represented by a.
Operations with Real Numbers
Perform the operations.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Find the length of the diagonal of a square with sides measuring 8 centimeters.
-
Find the length of the diagonal of a rectangle with sides measuring 6 centimeters and 12 centimeters.
Square and Cube Roots of Real Numbers
Simplify.
Use a calculator to approximate the following to the nearest thousandth.
-
-
-
-
-
-
-
-
-
-
-
-
-
where
-
where
-
where and
-
where and
-
where
-
where
-
where , , and
-
where , , and
-
where and
-
where
-
What is the simple interest earned on a 4 year investment of $4,500 at an annual interest rate of %?
-
James traveled at an average speed of 48 miles per hour for hours. How far did he travel?
-
The period of a pendulum T in seconds is given by the formula where L represents its length in feet. Approximate the period of a pendulum with length 2 feet. Round off to the nearest tenth of a foot.
-
The average distance d, in miles, a person can see an object is given by the formula where h represents the person’s height above the ground, measured in feet. What average distance can a person see an object from a height of 10 feet? Round off to the nearest tenth of a mile.
Algebraic Expressions and Formulas
Multiply.
Combine like terms.
Simplify.
Evaluate.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
The value of a new tablet computer in dollars can be estimated using the formula where t represents the number of years after it is purchased. Use the formula to estimate the value of the tablet computer years after it was purchased.
-
The speed of light is approximately miles per hour. Express this speed in miles per minute and determine the distance light travels in 4 minutes.
Rules of Exponents and Scientific Notation
Multiply.
Perform the operations.
Polynomials and Their Operations
Simplify.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Solve for s:
-
Solve for x:
-
A larger integer is 3 more than twice another. If their sum divided by 2 is 9, find the integers.
-
The sum of three consecutive odd integers is 171. Find the integers.
-
The length of a rectangle is 3 meters less than twice its width. If the perimeter measures 66 meters, find the length and width.
-
How long will it take $500 to earn $124 in simple interest earning 6.2% annual interest?
-
It took Sally hours to drive the 147 miles home from her grandmother’s house. What was her average speed?
-
Jeannine invested her bonus of $8,300 in two accounts. One account earned % simple interest and the other earned % simple interest. If her total interest for one year was $341.75, how much did she invest in each account?
Solving Linear Equations
Solve.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Jerry scored 90, 85, 92, and 76 on the first four algebra exams. What must he score on the fifth exam so that his average is at least 80?
-
If 6 degrees less than 3 times an angle is between 90 degrees and 180 degrees, then what are the bounds of the original angle?
Solving Linear Inequalities with One Variable
Solve. Graph all solutions on a number line and provide the corresponding interval notation.
Answers
-
-
-
-
-
-
-
-
-
;

-
-
;

-
-
;
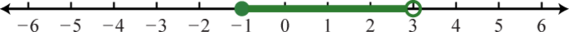
-
-
;
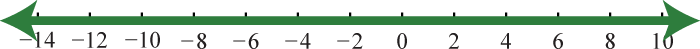
-
-
-
-
-
-
-
-
-
-
-
-
4
-
-
-
-
-
-
-
-
−4
-
-
-
-
−15
-
-
−6
-
-
−24
-
-
-
-
−50
-
-
14
-
-
-
-
0
-
-
-
-
-
-
-
-
-
-
3.464
-
-
2.621
-
-
centimeters
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
80
-
-
30
-
-
-
-
-
-
$855
-
-
1.6 seconds
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
$128.57
-
-
-
-
-
-
-
-
-
-
Ø
-
-
−3
-
-
-
-
-
-
-
-
5, 13
-
-
Length: 21 meters; Width: 12 meters
-
-
42 miles per hour
-
-
;

-
-
;
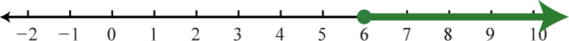
-
-
;

-
-
;
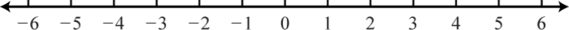
-
-
;

-
-
;

-
-
;

-
-
;

-
-
;

-
-
;

-
-
;

-
-
Jerry must score at least 57 on the fifth exam.
-
Sample Exam
-
-
-
-
-
Find the diagonal of a square with sides measuring 6 centimeters.
-
-
-
-
-
-
-
-
-
-
-
-
Solve for y:
-
-
-
-
-
Degrees Fahrenheit F is given by the formula where C represents degrees Celsius. What is the Fahrenheit equivalent to 35° Celsius?
-
The length of a rectangle is 5 inches less than its width. If the perimeter is 134 inches, find the length and width of the rectangle.
-
Melanie invested 4,500 in two separate accounts. She invested part in a CD that earned 3.2% simple interest and the rest in a savings account that earned 2.8% simple interest. If the total simple interest for one year was $138.80, how much did she invest in each account?
-
A rental car costs $45.00 per day plus $0.48 per mile driven. If the total cost of a one-day rental is to be at most $105, how many miles can be driven?
Simplify.
Simplify.
Solve.
Solve. Graph the solutions on a number line and give the corresponding interval notation.
Use algebra to solve the following.
Answers
-
38
-
-
-
-
centimeters
-
-
-
-
-
-
-
-
-
-
-
-
-
-
;
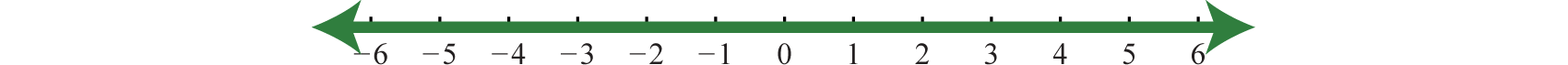
-
-
;

-
-
Length: 31 inches; width: 36 inches
-
-
The car can be driven at most 125 miles.




