This is “Polynomials and Their Operations”, section 1.6 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
1.6 Polynomials and Their Operations
Learning Objectives
- Identify a polynomial and determine its degree.
- Add and subtract polynomials.
- Multiply and divide polynomials.
Definitions
A polynomialAn algebraic expression consisting of terms with real number coefficients and variables with whole number exponents. is a special algebraic expression with terms that consist of real number coefficients and variable factors with whole number exponents. Some examples of polynomials follow:
The degree of a termThe exponent of the variable. If there is more than one variable in the term, the degree of the term is the sum their exponents. in a polynomial is defined to be the exponent of the variable, or if there is more than one variable in the term, the degree is the sum of their exponents. Recall that ; any constant term can be written as a product of and itself. Hence the degree of a constant term is 0.
Term |
Degree |
|---|---|
, since |
|
1, since |
The degree of a polynomialThe largest degree of all of its terms. is the largest degree of all of its terms.
Polynomial |
Degree |
|---|---|
, because has degree 4. |
|
1, because |
Of particular interest are polynomials with one variableA polynomial where each term has the form , where is any real number and n is any whole number., where each term is of the form Here is any real number and n is any whole number. Such polynomials have the standard form:
Typically, we arrange terms of polynomials in descending order based on the degree of each term. The leading coefficientThe coefficient of the term with the largest degree. is the coefficient of the variable with the highest power, in this case,
Example 1
Write in standard form:
Solution:
Since terms are defined to be separated by addition, we write the following:
In this form, we can see that the subtraction in the original corresponds to negative coefficients. Because addition is commutative, we can write the terms in descending order based on the degree as follows:
Answer:
We classify polynomials by the number of terms and the degree:
Expression |
Classification |
Degree |
|---|---|---|
Monomial (one term) |
7 |
|
Binomial (two terms) |
6 |
|
Trinomial (three terms) |
2 |
|
Polynomial (many terms) |
3 |
We can further classify polynomials with one variable by their degree:
Polynomial |
Name |
|---|---|
5 |
Constant (degree 0) |
Linear (degree 1) |
|
Quadratic (degree 2) |
|
Cubic (degree 3) |
|
Fourth-degree polynomial |
In this text, we call any polynomial of degree an nth-degree polynomial. In other words, if the degree is 4, we call the polynomial a fourth-degree polynomial. If the degree is 5, we call it a fifth-degree polynomial, and so on.
Example 2
State whether the following polynomial is linear or quadratic and give the leading coefficient:
Solution:
The highest power is 2; therefore, it is a quadratic polynomial. Rewriting in standard form we have
Here and thus the leading coefficient is −1.
Answer: Quadratic; leading coefficient: −1
Adding and Subtracting Polynomials
We begin by simplifying algebraic expressions that look like or Here, the coefficients are actually implied to be +1 and −1 respectively and therefore the distributive property applies. Multiply each term within the parentheses by these factors as follows:
Use this idea as a means to eliminate parentheses when adding and subtracting polynomials.
Example 3
Add:
Solution:
The property allows us to eliminate the parentheses, after which we can then combine like terms.
Answer:
Example 4
Add:
Solution:
Remember that the variable parts have to be exactly the same before we can add the coefficients.
Answer:
When subtracting polynomials, the parentheses become very important.
Example 5
Subtract:
Solution:
The property allows us to remove the parentheses after subtracting each term.
Answer:
Subtracting a quantity is equivalent to multiplying it by −1.
Example 6
Subtract:
Solution:
Distribute the −1, remove the parentheses, and then combine like terms. Multiplying the terms of a polynomial by −1 changes all the signs.

Answer:
Multiplying Polynomials
Use the product rule for exponents, , to multiply a monomial times a polynomial. In other words, when multiplying two expressions with the same base, add the exponents. To find the product of monomials, multiply the coefficients and add the exponents of variable factors with the same base. For example,
To multiply a polynomial by a monomial, apply the distributive property, and then simplify each term.
Example 7
Multiply:
Solution:
Apply the distributive property and then simplify.

Answer:
To summarize, multiplying a polynomial by a monomial involves the distributive property and the product rule for exponents. Multiply all of the terms of the polynomial by the monomial. For each term, multiply the coefficients and add exponents of variables where the bases are the same.
In the same manner that we used the distributive property to distribute a monomial, we use it to distribute a binomial. Here we apply the distributive property multiple times to produce the final result. This same result is obtained in one step if we apply the distributive property to a and b separately as follows:
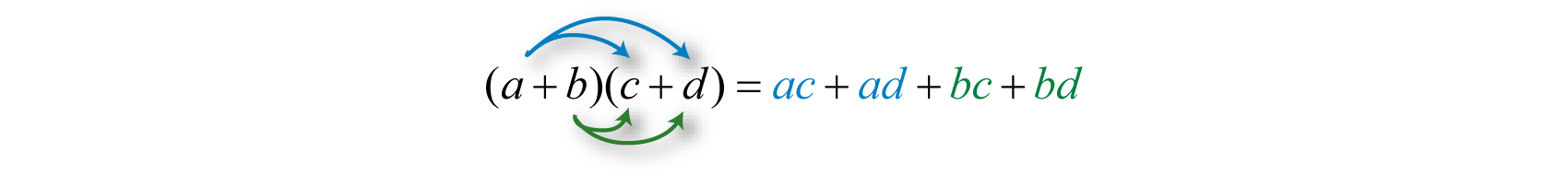
This is often called the FOIL method. Multiply the first, outer, inner, and then last terms.
Example 8
Multiply:
Solution:
Distribute 6x and −1 and then combine like terms.
Answer:
Consider the following two calculations:
This leads us to two formulas that describe perfect square trinomialsThe trinomials obtained by squaring the binomials and :
We can use these formulas to quickly square a binomial.
Example 9
Multiply:
Solution:
Here and Apply the formula:
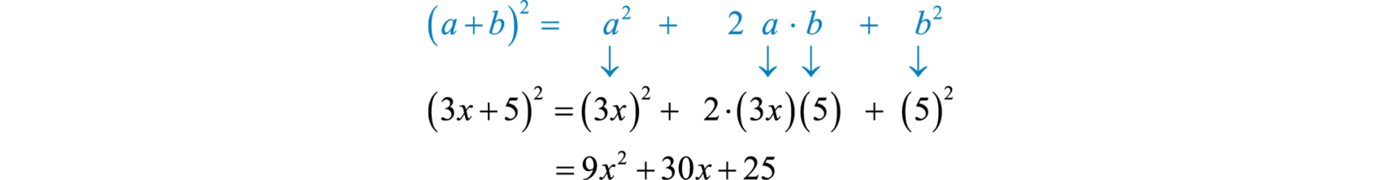
Answer:
This process should become routine enough to be performed mentally. Our third special product follows: This product is called difference of squaresThe special product obtained by multiplying conjugate binomials :
The binomials and are called conjugate binomialsThe binomials and . When multiplying conjugate binomials the middle terms are opposites and their sum is zero; the product is itself a binomial.
Example 10
Multiply:
Solution:
Answer:
Example 11
Multiply:
Solution:
Here we perform one product at a time.

Answer:
Dividing Polynomials
Use the quotient rule for exponents, , to divide a polynomial by a monomial. In other words, when dividing two expressions with the same base, subtract the exponents. In this section, we will assume that all variables in the denominator are nonzero.
Example 12
Divide:
Solution:
Divide the coefficients and apply the quotient rule by subtracting the exponents of the like bases.
Answer:
When dividing a polynomial by a monomial, we may treat the monomial as a common denominator and break up the fraction using the following property: Applying this property will result in terms that can be treated as quotients of monomials.
Example 13
Divide:
Solution:
Break up the fraction by dividing each term in the numerator by the monomial in the denominator, and then simplify each term.
Answer:
We can check our division by multiplying our answer, the quotient, by the monomial in the denominator, the divisor, to see if we obtain the original numerator, the dividend.
or |
or |
The same technique outlined for dividing by a monomial does not work for polynomials with two or more terms in the denominator. In this section, we will outline a process called polynomial long divisionThe process of dividing two polynomials using the division algorithm., which is based on the division algorithm for real numbers. For the sake of clarity, we will assume that all expressions in the denominator are nonzero.
Example 14
Divide:
Solution:
Here is the divisor and is the dividend. To determine the first term of the quotient, divide the leading term of the dividend by the leading term of the divisor.

Multiply the first term of the quotient by the divisor, remembering to distribute, and line up like terms with the dividend.

Subtract the resulting quantity from the dividend. Take care to subtract both terms.

Bring down the remaining terms and repeat the process.
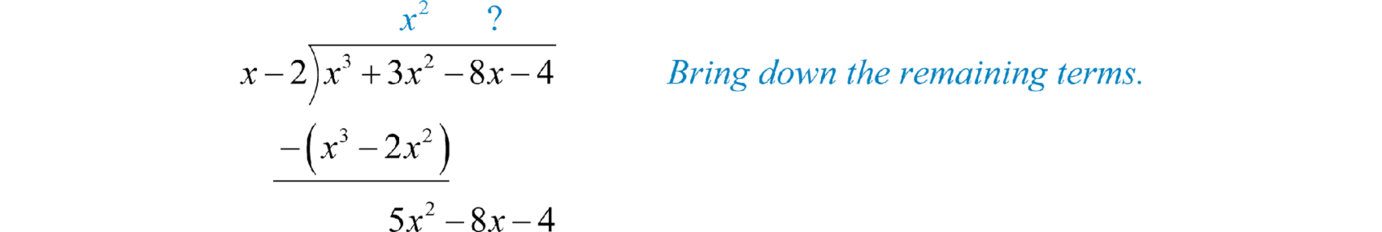
Notice that the leading term is eliminated and that the result has a degree that is one less. The complete process is illustrated below:
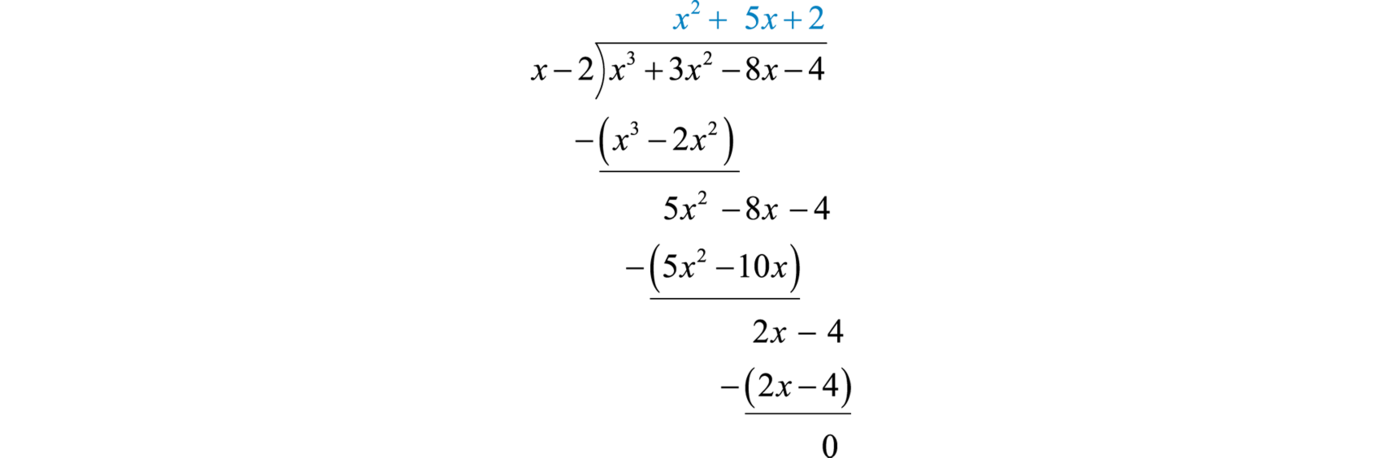
Polynomial long division ends when the degree of the remainder is less than the degree of the divisor. Here, the remainder is 0. Therefore, the binomial divides the polynomial evenly and the answer is the quotient shown above the division bar.
To check the answer, multiply the divisor by the quotient to see if you obtain the dividend as illustrated below:
This is left to the reader as an exercise.
Answer:
Next, we demonstrate the case where there is a nonzero remainder.

Just as with real numbers, the final answer adds to the quotient the fraction where the remainder is the numerator and the divisor is the denominator. In general, when dividing we have: If we multiply both sides by the divisor we obtain,
Example 15
Divide:
Solution:
Since the denominator is a binomial, begin by setting up polynomial long division.
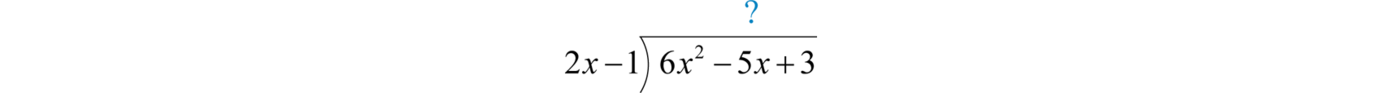
To start, determine what monomial times results in a leading term This is the quotient of the given leading terms: Multiply times the divisor , and line up the result with like terms of the dividend.
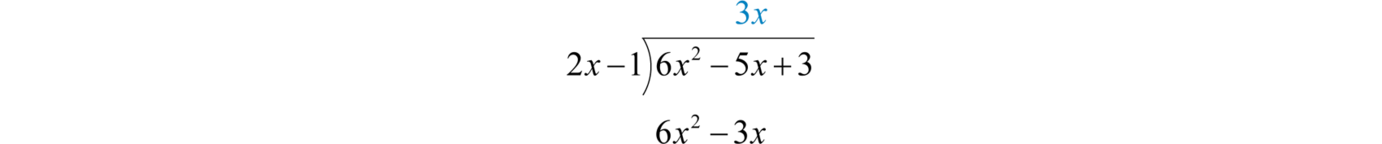
Subtract the result from the dividend and bring down the constant term +3.
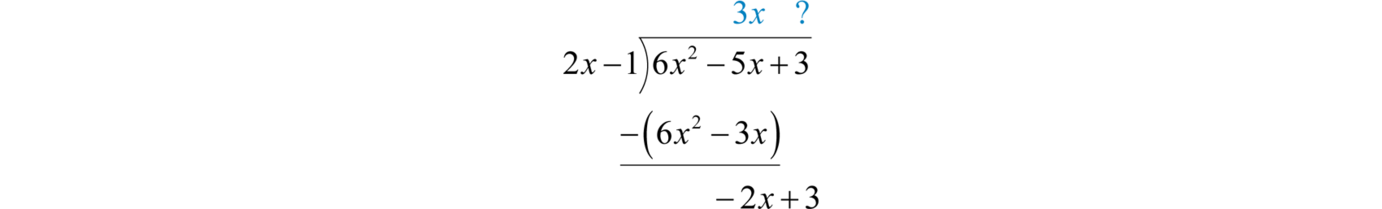
Subtracting eliminates the leading term. Multiply by −1 and line up the result.
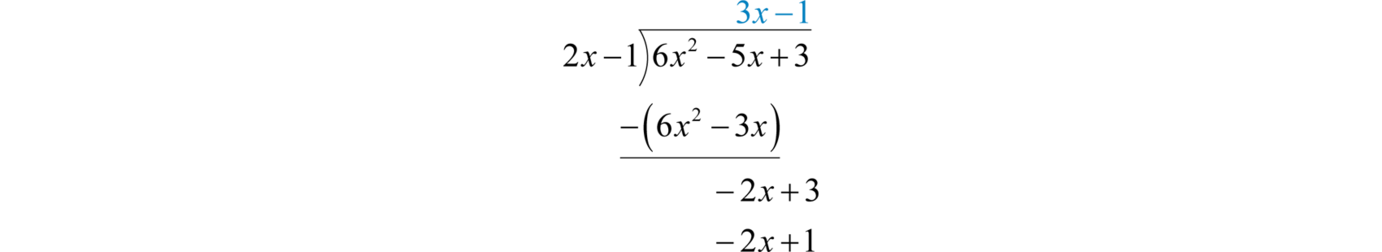
Subtract again and notice that we are left with a remainder.
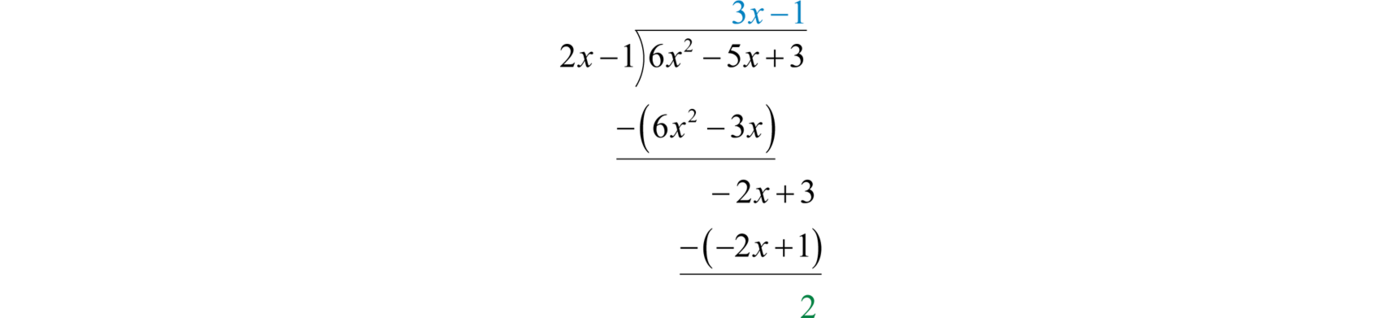
The constant term 2 has degree 0 and thus the division ends. Therefore,
To check that this result is correct, we multiply as follows:
Answer:
Occasionally, some of the powers of the variables appear to be missing within a polynomial. This can lead to errors when lining up like terms. Therefore, when first learning how to divide polynomials using long division, fill in the missing terms with zero coefficients, called placeholdersTerms with zero coefficients used to fill in all missing exponents within a polynomial..
Example 16
Divide:
Solution:
Notice that the binomial in the numerator does not have terms with degree 2 or 1. The division is simplified if we rewrite the expression with placeholders:
Set up polynomial long division:
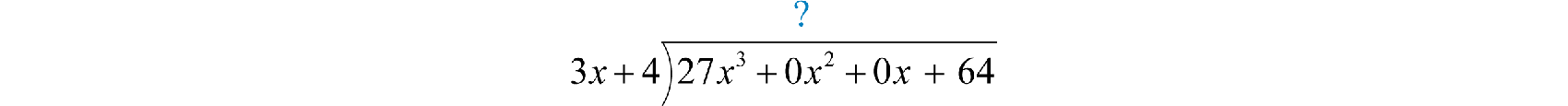
We begin with and work the rest of the division algorithm.
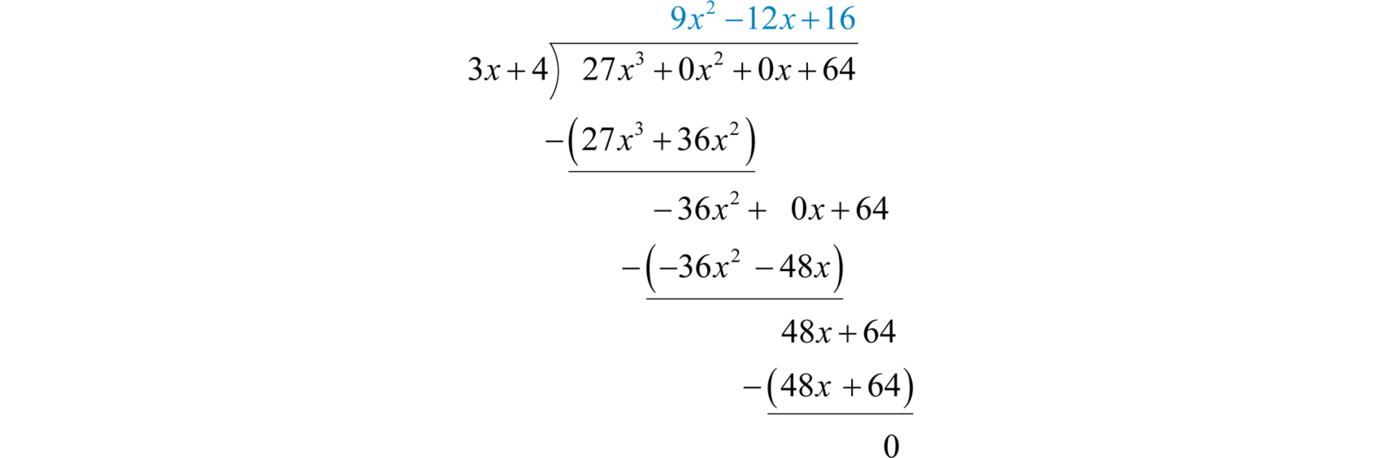
Answer:
Example 17
Divide:
Solution:
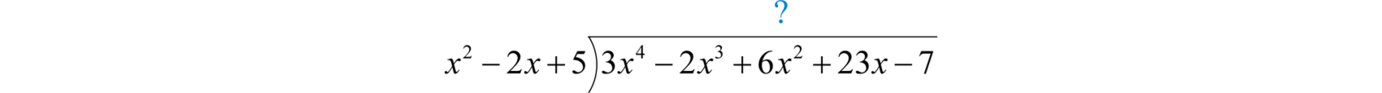
Begin the process by dividing the leading terms to determine the leading term of the quotient Take care to distribute and line up the like terms. Continue the process until the remainder has a degree less than 2.
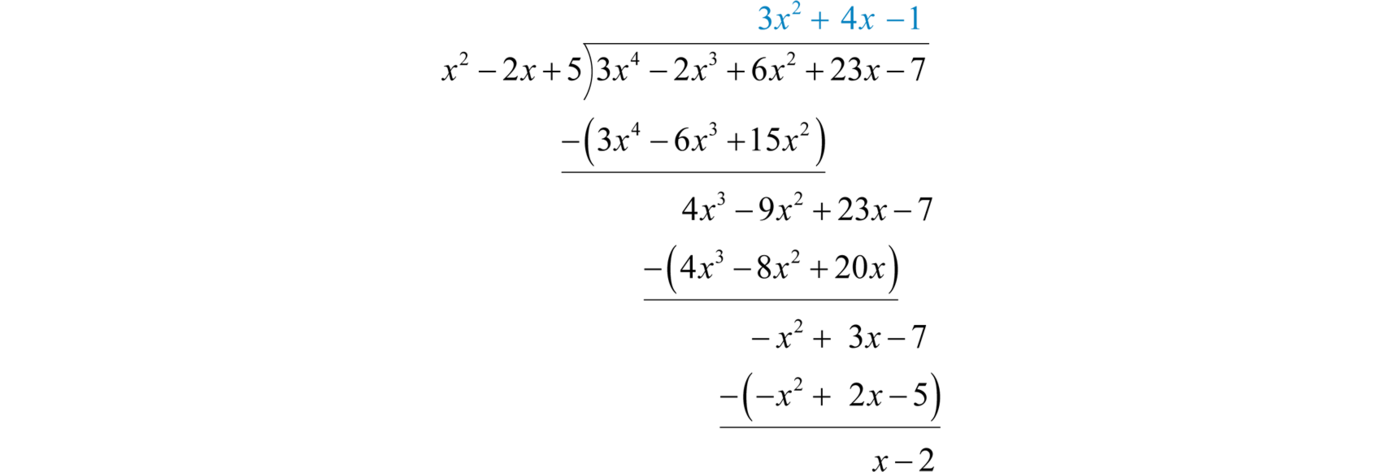
The remainder is Write the answer with the remainder:
Answer:
Polynomial long division takes time and practice to master. Work lots of problems and remember that you may check your answers by multiplying the quotient by the divisor (and adding the remainder if present) to obtain the dividend.
Key Takeaways
- Polynomials are special algebraic expressions where the terms are the products of real numbers and variables with whole number exponents.
- The degree of a polynomial with one variable is the largest exponent of the variable found in any term. In addition, the terms of a polynomial are typically arranged in descending order based on the degree of each term.
- When adding polynomials, remove the associated parentheses and then combine like terms. When subtracting polynomials, distribute the −1, remove the parentheses, and then combine like terms.
- To multiply polynomials apply the distributive property; multiply each term in the first polynomial with each term in the second polynomial. Then combine like terms.
- When dividing by a monomial, divide all terms in the numerator by the monomial and then simplify each term.
- When dividing a polynomial by another polynomial, apply the division algorithm.
Topic Exercises
-
-
-
-
-
-
-
-
-
-
-
-
5
-
-
-
-
-
-
-
-
Part A: Definitions
Write the given polynomials in standard form.
Classify the given polynomial as a monomial, binomial, or trinomial and state the degree.
State whether the polynomial is linear or quadratic and give the leading coefficient.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Subtract from
-
Subtract from
-
A right circular cylinder has a height that is equal to the radius of the base, Find a formula for the surface area in terms of h.
-
A rectangular solid has a width that is twice the height and a length that is 3 times that of the height. Find a formula for the surface area in terms of the height.
Part B: Adding and Subtracting Polynomials
Simplify.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Find the product of and
-
Find the product of and
-
Each side of a square measures units. Determine the area in terms of x.
-
Each edge of a cube measures units. Determine the volume in terms of x.
Part C: Multiplying Polynomials
Multiply.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Find the quotient of and
-
Find the quotient of and
Part D: Dividing Polynomials
Divide.
Answers
-
-
-
-
-
-
-
Trinomial; degree 2
-
-
Trinomial; degree 4
-
-
Binomial; degree 4
-
-
Quadratic, −9
-
-
Linear, 2
-
-
Quadratic, 5
-
-
Quadratic, −2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
square units
-




