This is “Review of Real Numbers and Absolute Value”, section 1.1 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
1.1 Review of Real Numbers and Absolute Value
Learning Objectives
- Review the set of real numbers.
- Review the real number line and notation.
- Define the geometric and algebraic definition of absolute value.
Real Numbers
Algebra is often described as the generalization of arithmetic. The systematic use of variablesLetters used to represent numbers., letters used to represent numbers, allows us to communicate and solve a wide variety of real-world problems. For this reason, we begin by reviewing real numbers and their operations.
A setAny collection of objects. is a collection of objects, typically grouped within braces { }, where each object is called an elementAn object within a set.. When studying mathematics, we focus on special sets of numbers.
The three periods (…) are called an ellipsis and indicate that the numbers continue without bound. A subsetA set consisting of elements that belong to a given set., denoted , is a set consisting of elements that belong to a given set. Notice that the sets of naturalThe set of counting numbers: {1, 2, 3, 4, 5, …}. and whole numbersThe set of natural numbers combined with zero: {0, 1, 2, 3, 4, 5, …}. are both subsets of the set of integers and we can write:
A set with no elements is called the empty setA subset with no elements, denoted Ø or { }. and has its own special notation:
Rational numbersNumbers of the form , where a and b are integers and b is nonzero., denoted , are defined as any number of the form where a and b are integers and b is nonzero. We can describe this set using set notationNotation used to describe a set using mathematical symbols.:
The vertical line | inside the braces reads, “such that” and the symbol indicates set membership and reads, “is an element of.” The notation above in its entirety reads, “the set of all numbers such that a and b are elements of the set of integers and b is not equal to zero.” Decimals that terminate or repeat are rational. For example,
The set of integers is a subset of the set of rational numbers, , because every integer can be expressed as a ratio of the integer and 1. In other words, any integer can be written over 1 and can be considered a rational number. For example,
Irrational numbersNumbers that cannot be written as a ratio of two integers. are defined as any numbers that cannot be written as a ratio of two integers. Nonterminating decimals that do not repeat are irrational. For example,
Finally, the set of real numbersThe set of all rational and irrational numbers., denoted , is defined as the set of all rational numbers combined with the set of all irrational numbers. Therefore, all the numbers defined so far are subsets of the set of real numbers. In summary,

The set of even integersIntegers that are divisible by 2. is the set of all integers that are evenly divisible by 2. We can obtain the set of even integers by multiplying each integer by 2.
The set of odd integersNonzero integers that are not divisible by 2. is the set of all nonzero integers that are not evenly divisible by 2.
A prime numberInteger greater than 1 that is divisible only by 1 and itself. is an integer greater than 1 that is divisible only by 1 and itself. The smallest prime number is 2 and the rest are necessarily odd.
Any integer greater than 1 that is not prime is called a composite numberIntegers greater than 1 that are not prime. and can be uniquely written as a product of primes. When a composite number, such as 42, is written as a product, , we say that is a factorizationAny combination of factors, multiplied together, resulting in the product. of 42 and that 2 and 21 are factorsAny of the numbers that form a product.. Note that factors divide the number evenly. We can continue to write composite factors as products until only a product of primes remains.

Therefore, the prime factorizationThe unique factorization of a natural number written as a product of primes. of 42 is
Example 1
Determine the prime factorization of 210.
Solution:
Begin by writing 210 as a product with 10 as a factor. Then continue factoring until only a product of primes remains.
Since the prime factorization is unique, it does not matter how we choose to initially factor the number; the end result will be the same.
Answer:
A fractionA rational number written as a quotient of two integers: , where is a rational number written as a quotient, or ratio, of two integers a and b where .

The integer above the fraction bar is called the numeratorThe number above the fraction bar. and the integer below is called the denominatorThe number below the fraction bar.. Two equal ratios expressed using different numerators and denominators are called equivalent fractionsTwo equal fractions expressed using different numerators and denominators.. For example,
Consider the following factorizations of 50 and 100:
The numbers 50 and 100 share the factor 25. A shared factor is called a common factorA factor that is shared by more than one real number.. Making use of the fact that , we have
Dividing and replacing this factor with a 1 is called cancellingThe process of dividing out common factors in the numerator and the denominator.. Together, these basic steps for finding equivalent fractions define the process of reducingThe process of finding equivalent fractions by dividing the numerator and the denominator by common factors.. Since factors divide their product evenly, we achieve the same result by dividing both the numerator and denominator by 25 as follows:
Finding equivalent fractions where the numerator and denominator are relatively primeNumbers that have no common factor other than 1., or have no common factor other than 1, is called reducing to lowest termsFinding equivalent fractions where the numerator and the denominator share no common integer factor other than 1.. This can be done by dividing the numerator and denominator by the greatest common factor (GCF).The largest shared factor of any number of integers. The GCF is the largest number that divides a set of numbers evenly. One way to find the GCF of 50 and 100 is to list all the factors of each and identify the largest number that appears in both lists. Remember, each number is also a factor of itself.
Common factors are listed in bold, and we see that the greatest common factor is 50. We use the following notation to indicate the GCF of two numbers: GCF(50, 100) = 50. After determining the GCF, reduce by dividing both the numerator and the denominator as follows:
Example 2
Reduce to lowest terms:
Solution:
A quick way to find the GCF of the numerator and denominator requires us to first write each as a product of primes. The GCF will be the product of all the common prime factors.
In this case, the product of the common prime factors is 36.
We can convert the improper fraction to a mixed number ; however, it is important to note that converting to a mixed number is not part of the reducing process. We consider improper fractions, such as , to be reduced to lowest terms. In algebra it is often preferable to work with improper fractions, although in some applications, mixed numbers are more appropriate.
Answer:
Recall the relationship between multiplication and division:
In this case, the dividendA number to be divided by another number. 12 is evenly divided by the divisorThe number that is divided into the dividend. 6 to obtain the quotientThe result of division. 2. It is true in general that if we multiply the divisor by the quotient we obtain the dividend. Now consider the case where the dividend is zero and the divisor is nonzero:
This demonstrates that zero divided by any nonzero real number must be zero. Now consider a nonzero number divided by zero:
Zero times anything is zero and we conclude that there is no real number such that Thus, the quotient is undefinedA quotient such as is left without meaning and is not assigned an interpretation.. Try it on a calculator, what does it say? For our purposes, we will simply write “undefined.” To summarize, given any real number , then
We are left to consider the case where the dividend and divisor are both zero.
Here, any real number seems to work. For example, and also, Therefore, the quotient is uncertain or indeterminateA quotient such as is a quantity that is uncertain or ambiguous..
In this course, we state that is undefined.
The Number Line and Notation
A real number lineA line that allows us to visually represent real numbers by associating them with points on the line., or simply number line, allows us to visually display real numbers by associating them with unique points on a line. The real number associated with a point is called a coordinateThe real number associated with a point on a number line.. A point on the real number line that is associated with a coordinate is called its graphA point on the number line associated with a coordinate.. To construct a number line, draw a horizontal line with arrows on both ends to indicate that it continues without bound. Next, choose any point to represent the number zero; this point is called the originThe point on the number line that represents zero..
Positive real numbers lie to the right of the origin and negative real numbers lie to the left. The number zero (0) is neither positive nor negative. Typically, each tick represents one unit.
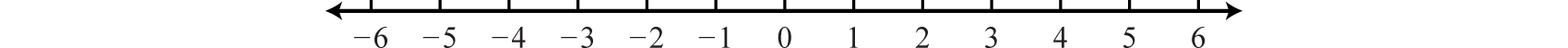
As illustrated below, the scale need not always be one unit. In the first number line, each tick mark represents two units. In the second, each tick mark represents :
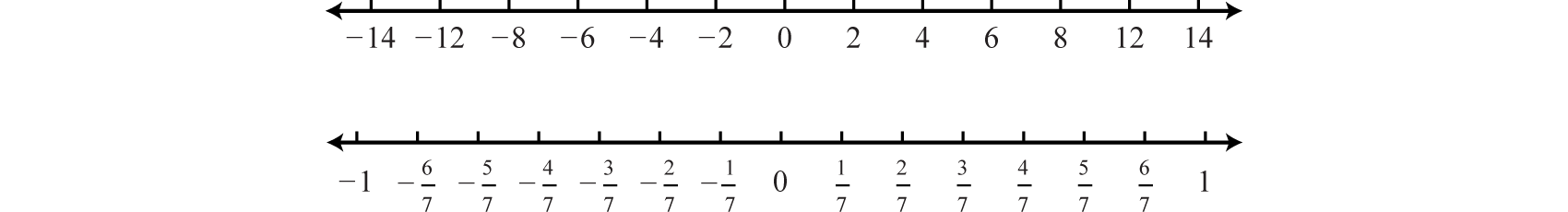
The graph of each real number is shown as a dot at the appropriate point on the number line. A partial graph of the set of integers , follows:

Example 3
Graph the following set of real numbers:
Solution:
Graph the numbers on a number line with a scale where each tick mark represents unit.
Answer:
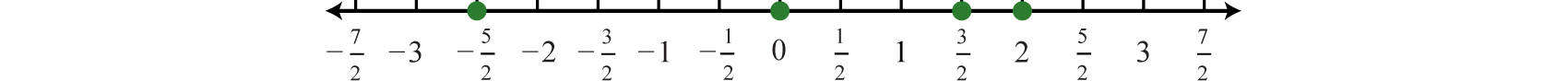
The oppositeReal numbers whose graphs are on opposite sides of the origin with the same distance to the origin. of any real number a is −a. Opposite real numbers are the same distance from the origin on a number line, but their graphs lie on opposite sides of the origin and the numbers have opposite signs.
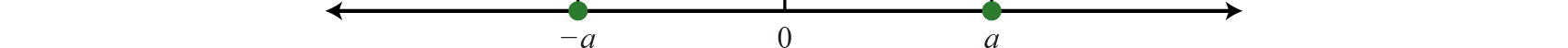
Given the integer −7, the integer the same distance from the origin and with the opposite sign is +7, or just 7.

Therefore, we say that the opposite of −7 is −(−7) = 7. This idea leads to what is often referred to as the double-negative propertyThe opposite of a negative number is positive: −(−a) = a.. For any real number a,
Example 4
Calculate:
Solution:
Here we apply the double-negative within the innermost parentheses first.
Answer:
In general, an odd number of sequential negative signs results in a negative value and an even number of sequential negative signs results in a positive value.
When comparing real numbers on a number line, the larger number will always lie to the right of the smaller one. It is clear that 15 is greater than 5, but it may not be so clear to see that −1 is greater than −5 until we graph each number on a number line.
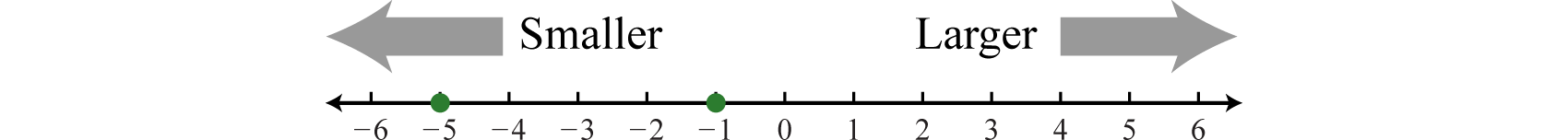
We use symbols to help us efficiently communicate relationships between numbers on the number line.
The relationship between the integersThe set of positive and negative whole numbers combined with zero: {…, −3, −2, −1, 0, 1, 2, 3, …}. in the previous illustration can be expressed two ways as follows:
The symbols < and > are used to denote strict inequalitiesExpress ordering relationships using the symbol < for “less than” and > for “greater than.”, and the symbols and are used to denote inclusive inequalitiesUse the symbol to express quantities that are “less than or equal to” and for quantities that are “greater than or equal to” each other.. In some situations, more than one symbol can be correctly applied. For example, the following two statements are both true:
In addition, the “or equal to” component of an inclusive inequality allows us to correctly write the following:
The logical use of the word “or” requires that only one of the conditions need be true: the “less than” or the “equal to.”
Example 5
Fill in the blank with <, =, or >:
Solution:
Use > because the graph of −2 is to the right of the graph of −12 on a number line. Therefore, −2 > −12, which reads, “negative two is greater than negative twelve.”

Answer: −2 > −12
An algebraic inequalityAlgebraic expressions related with the symbols , <, , and >., such as , is read, “x is greater than or equal to 2.” Here the letter x is a variable, which can represent any real number. However, the statement imposes a condition on the variable. SolutionsValues that can be used in place of the variable to satisfy the given condition. are the values for x that satisfy the condition. This inequality has infinitely many solutions for x, some of which are 2, 3, 4.1, 5, 20, and 20.001. Since it is impossible to list all of the solutions, a system is needed that allows a clear communication of this infinite set. Common ways of expressing solutions to an inequality are by graphing them on a number line, using interval notation, or using set notation.
To express the solution graphically, draw a number line and shade in all the values that are solutions to the inequality. This is called the graph of the solution setSolutions to an algebraic expression expressed on a number line.. Interval and set notation follow:

In this example, there is an inclusive inequality, which means that the lower-bound 2 is included in the solution set. Denote this with a closed dot on the number line and a square bracket in interval notation. The symbol ∞ is read as “infinityThe symbol ∞ indicates the interval is unbounded to the right.” and indicates that the set is unbounded to the right on a number line. If using a standard keyboard, use (inf) as a shortened form to denote infinity. Now compare the notation in the previous example to that of the strict, or noninclusive, inequality that follows:

Strict inequalities imply that solutions may get very close to the boundary point, in this case 3, but not actually include it. Denote this idea with an open dot on the number line and a round parenthesis in interval notation. The symbol −∞ is read as “negative infinityThe symbol −∞ indicates the interval is unbounded to the left.” and indicates that the set is unbounded to the left on a number line. Infinity is a bound to the real numbers, but is not itself a real number: it cannot be included in the solution set and thus is always enclosed with a parenthesis.
Interval notation is textual and is determined after graphing the solution set on a number line. The numbers in interval notation should be written in the same order as they appear on the number line, with smaller numbers in the set appearing first. Set notation, sometimes called set-builder notation, allows us to describe the set using familiar mathematical notation. For example,
Here, describes the type of number. This implies that the variable x represents a real number. The statement is the condition that describes the set using mathematical notation. At this point in our study of algebra, it is assumed that all variables represent real numbers. For this reason, you can omit the “”, and write
Example 6
Graph the solution set and give the interval and set notation equivalents:
Solution:
Use an open dot at −20, because of the strict inequality <, and shade all real numbers to the left.
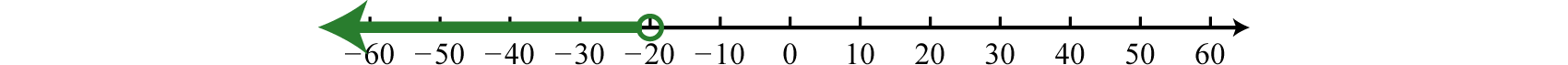
Answer: Interval notation: ; set notation:
A compound inequalityTwo or more inequalities in one statement joined by the word “and” or by the word “or.” is actually two or more inequalities in one statement joined by the word “and” or by the word “or”. Compound inequalities with the logical “or” require that either condition must be satisfied. Therefore, the solution set of this type of compound inequality consists of all the elements of the solution sets of each inequality. When we join these individual solution sets it is called the unionThe set formed by joining the individual solution sets indicated by the logical use of the word “or” and denoted with the symbol , denoted For example,
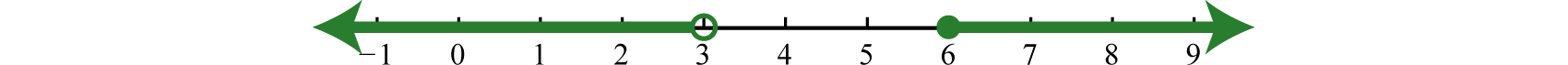
An inequality such as, reads, “negative one is less than or equal to x and x is less than three.” This is actually a compound inequality because it can be decomposed as follows:
The logical “and” requires that both conditions must be true. Both inequalities will be satisfied by all the elements in the intersectionThe set formed by the shared values of the individual solution sets that is indicated by the logical use of the word “and,” denoted with the symbol , denoted , of the solution sets of each.
Example 7
Graph and give the interval notation equivalent:
Solution:
Determine the intersection, or overlap, of the two solution sets to and The solutions to each inequality are sketched above the number line as a means to determine the intersection, which is graphed on the number line below.
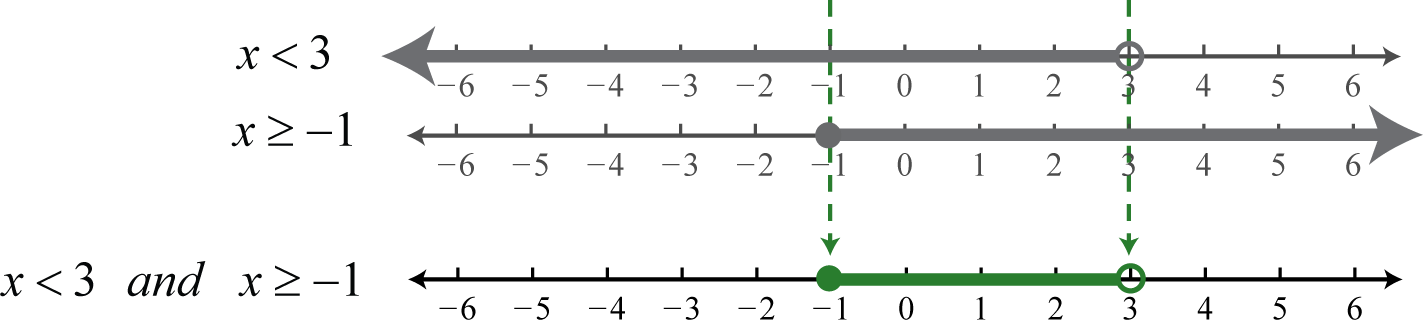
Here, 3 is not a solution because it solves only one of the inequalities. Alternatively, we may interpret as all possible values for x between, or bounded by, −1 and 3 where −1 is included in the solution set.
Answer: Interval notation: ; set notation:
In this text, we will often point out the equivalent notation used to express mathematical quantities electronically using the standard symbols available on a keyboard.
Many calculators, computer algebra systems, and programming languages use the notation presented above, in quotes.
Absolute Value
The absolute valueThe absolute value of a number represents the distance from the graph of the number to zero on a number line. of a real number a, denoted , is defined as the distance between zero (the origin) and the graph of that real number on the number line. Since it is a distance, it is always positive. For example,
Both 4 and −4 are four units from the origin, as illustrated below:
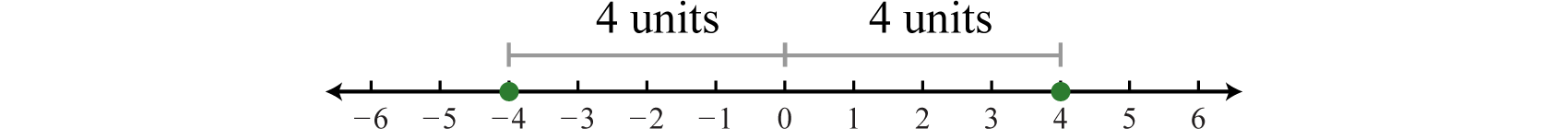
Also, it is worth noting that,
The algebraic definition of the absolute value of a real number a follows:
This is called a piecewise definitionA definition that changes depending on the value of the variable.. The result depends on the quantity a. If a is nonnegative, as indicated by the inequality , then the absolute value will be that number a. If a is negative, as indicated by the inequality , then the absolute value will be the opposite of that number, −a. The results will be the same as the geometric definition. For example, to determine we make note that the value is negative and use the second part of the definition. The absolute value will be the opposite of −4.
At this point, we can determine what real numbers have certain absolute values.
Example 8
Determine the values represented by x:
Solution:
Think of a real number whose distance to the origin is 6 units. There are two solutions: the distance to the right of the origin and the distance to the left of the origin, namely The symbol ± is read “plus or minus” and indicates that there are two answers, one positive and one negative.
Answer:
Example 9
Determine the values represented by x:
Solution:
Here we wish to find a value where the distance to the origin is negative. Since negative distance is not defined, this equation has no solution. Use the empty set Ø to denote this.
Answer: Ø
The absolute value can be expressed textually using the notation abs(a). We often encounter negative absolute values, such as or −abs(3). Notice that the negative sign is in front of the absolute value symbol. In this case, work the absolute value first and then find the opposite of the result.
Try not to confuse this with the double negative property, which states that
Example 10
Simplify:
Solution:
First, find the absolute value of −50 and then apply the double-negative property.
Answer: 50
Key Takeaways
- Algebra is often described as the generalization of arithmetic. The systematic use of variables, used to represent real numbers, allows us to communicate and solve a wide variety of real-world problems. Therefore, it is important to review the subsets of real numbers and their properties.
- The number line allows us to visually display real numbers by associating them with unique points on a line.
- Special notation is used to communicate equality and order relationships between numbers on a number line.
- The absolute value of a real number is defined geometrically as the distance between zero and the graph of that number on a number line. Alternatively, the absolute value of a real number is defined algebraically in a piecewise manner. If a real number a is nonnegative, then the absolute value will be that number a. If a is negative, then the absolute value will be the opposite of that number, −a.
Topic Exercises
-
Every other positive odd number up to 21.
-
Every other positive even number up to 22.
-
The even prime numbers.
-
Rational numbers that are also irrational.
-
The set of negative integers.
-
The set of negative even integers.
-
Three consecutive odd integers starting with 13.
-
Three consecutive even integers starting with 22.
-
195
-
78
-
330
-
273
-
180
-
350
-
-
-
-
-
-
-
-
-
-
Part A: Real Numbers
Use set notation to list the described elements.
Determine the prime factorization of the given composite number.
Reduce to lowest terms.
-
{−5, 5, 10, 15}
-
{−4, −2, 0, 2, 4}
-
-
-
{−5,−4,−3,−1, 1}
-
{−40, −30, −20, 10, 30}
-
−(−10)
-
-
−(−(−12))
-
-
-
-
−10 _____ −15
-
−101 _____ −100
-
−33 _____ 0
-
0 _____ −50
-
−(−(−2)) _____ −(−3)
-
_____
-
_____
-
_____
-
-
-
is irrational.
-
0 is a nonnegative number.
-
Any integer is a rational number.
-
The constant is rational.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
All real numbers less than −15.
-
All real numbers greater than or equal to −7.
-
All real numbers less than 6 and greater than zero.
-
All real numbers less than zero and greater than −5.
-
All real numbers less than or equal to 5 or greater than 10.
-
All real numbers between −2 and 2.
-
-
-
-
-
-
-
-
-
-
-
-
Part B: Number Line and Notation
Graph the following sets of numbers.
Simplify.
Fill in the blank with <, =, or >.
True or False.
Graph the solution set and give the interval notation equivalent.
Write an equivalent inequality.
Determine the inequality given the answers expressed in interval notation.
Part C: Absolute Value
Simplify.
Determine the values represented by a.
-
Research and discuss the origins and evolution of algebra.
-
Research and discuss reasons why algebra is a required subject today.
-
Solution sets to inequalities can be expressed using a graph, interval notation, or set notation. Discuss the merits and drawbacks of each method. Which do you prefer?
-
Research and discuss the Fundamental Theorem of Algebra. Illustrate its idea with an example and share your results.
Part D: Discussion Board
Answers
-
{1, 5, 9, 13, 17, 21}
-
-
{2}
-
-
{…,−3, −2, −1}
-
-
{13, 15, 17}
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
0
-
-

-
-
-
-
-
-
10
-
-
−12
-
-
-
-
>
-
-
<
-
-
<
-
-
<
-
-
True
-
-
False
-
-
True
-
-
(−∞, −1);
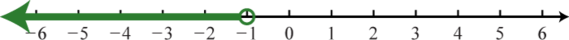
-
-
;

-
-
;

-
-
;

-
-
;

-
-
;

-
-
;
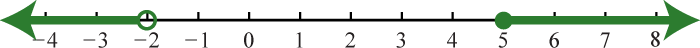
-
-
;

-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
-
-
−4
-
-
-
-
−7
-
-
2
-
-
5
-
-
-
-
-
-
-
-
Answer may vary
-
-
Answer may vary
-




